北师大版七年级数学下册1.6 乘法公式——完全平方公式 课件(共21张)
文档属性
| 名称 | 北师大版七年级数学下册1.6 乘法公式——完全平方公式 课件(共21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 870.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 11:01:39 | ||
图片预览




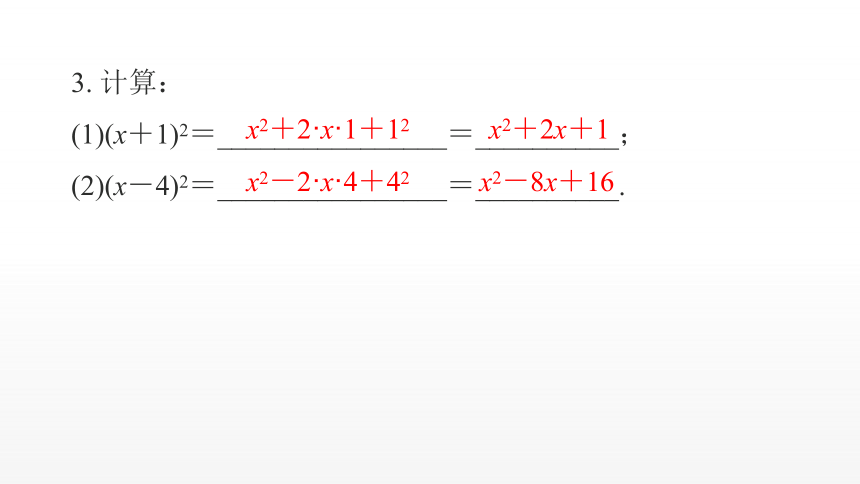




文档简介
第10课 乘法公式——完全平方公式
一、知识储备
1. 计算并探索规律:
(1)(a+b)(a+b);
(2)(a-b)(a-b).
解:原式=a2+ab+ba+b2=a2+2ab+b2
解:原式=a2-ab-ba+b2=a2-2ab+b2
二、新课学习
知识点1:利用完全平方公式计算
完全平方公式:(1)(a+b)2=________________;
(2)(a-b)2=________________.
口诀:首平方+尾平方,首尾乘积2倍放中央.
请你根据右图解释公式.
a2+2ab+b2
a2-2ab+b2
解:a2+ab+ab+b2=(a+b)2.
2.(例1)计算:
(1)(x+3)2=x2+2·x·3+32=__________;
(2)(x-5)2=________________=__________.
x2-10x+25
x2+6x+9
x2-2·x·5+52
3. 计算:
(1)(x+1)2=________________=__________;
(2)(x-4)2=________________=__________.
x2-8x+16
x2+2·x·1+12
x2+2x+1
x2-2·x·4+42
4.(例2)计算:
(1)(3x+5y)2;
解:原式=(3x)2+2·3x·5y+(5y)2
=9x2+30xy+25y2
解:原式=(2x)2-2·2x·
=4x2-2x+
5. 计算:
(1)(4x-3y)2;
解:原式=(4x)2-2·4x·3y+(3y)2
=16x2-24xy+9y2
解:原式
6.(例3)计算:
(1)(-x+5)2;
(2)(-2x-y)2.
解: 原式=(-x)2+2·(-x)·5+52
=x2-10x+25
解:原式=(-2x)2-2·(-2x)·y+y2
=4x2+4xy+y2
7. 计算:
(1)(-x-3)2;
(2)(-m+3n)2.
解:原式=(-x)2-2·(-x)·3+32
=x2+6x+9
解:原式=(-m)2+2·(-m)·3n+(3n)2
=m2-6mn+9n2
知识点2:多项式乘以多项式的综合计算
8.(例4)计算:(x+5)2-(x-2)(x+3).
解:原式=x2+10x+25-(x2+x-6)
=x2+10x+25-x2-x+6
=9x+31
9. 计算:(2x+y)(2x-y)-(2x+y)2.
解:原式=4x2-y2-(4x2+4xy+y2)
=4x2-y2-4x2-4xy-y2
=-4xy-2y2
三、过关检测
第1关
10. 计算(a-2)2的结果是( )
A. a2-4a+4
B. a2-2a+4
C. a2-4
D. a2-4a-4
A
11. 若(x+3)2=x2-ax+9,则a的值是( )
A. 3 B. -3 C. 6 D. -6
D
12. 下列计算正确的是( )
A. (a+3)2=a2+9
B. (x-1)2=x2-1
C. (x-2)(x+3)=x2-6
D. (x+1)(x-1)=x2-1
D
13. 计算:
(1)(3x+2)2= ;
(2)(mn-3)2= ;
(3)( x-2y)2= .
9x2+12x+4
m2n2-6mn+9
x2-2xy+4y2
14. 计算:
(1)(n+4)2-n2;
(2)(-2a+1)2.
解:原式=n2+8n+16-n2
=8n+16
解:原式=(-2a)2+2·(-2a)+12
=4a2-4a+1
15. 运用完全平方公式进行简便运算:
(1)1022; (2)1972.
解:原式=(100+2)2
=1002+2×100×2+22
=10 000+400+4
=10 404
解:原式=(200-3)2
=2002-2×200×3+32
=40 000-1 200+9
=38 809
第2关
16. 化简求值:(x+2)2+(2x+1)(2x-1)-4x(x+1),其中,x=-2.
解:原式=(x2+4x+4)+(4x2-1)-(4x2+4x)
=x2+4x+4+4x2-1-4x2-4x
=x2+3
当x=-2时,原式=(-2)2+3=7
17.如图,根据图形的面积关系可以验证的公式是( )
A. (a-b)(a+b)=a2-b2
B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2
D. a2-b2=(a-b)(a+b)
C
第3关
18. 一个圆的半径长为r(r>2) cm,减少2 cm后,这个圆的面积减少了多少?
解:∵圆的半径长为r(r>2) cm,减少2 cm后的半径变为
(r-2) cm.
则半径减少后圆的面积为:
π(r-2)2=π(r2-4r+4)=πr2-4πr+4π.
∴圆的面积减少了:πr2-(πr2-4πr+4π)=(4πr-4π) cm2.
19.如图的三角形可解释(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
其中(a+b)0=1,
(a+b)1=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
根据“杨辉三角”计算(a+b)4.
解:原式=a4+4a3b+6a2b2+4ab3+b4
一、知识储备
1. 计算并探索规律:
(1)(a+b)(a+b);
(2)(a-b)(a-b).
解:原式=a2+ab+ba+b2=a2+2ab+b2
解:原式=a2-ab-ba+b2=a2-2ab+b2
二、新课学习
知识点1:利用完全平方公式计算
完全平方公式:(1)(a+b)2=________________;
(2)(a-b)2=________________.
口诀:首平方+尾平方,首尾乘积2倍放中央.
请你根据右图解释公式.
a2+2ab+b2
a2-2ab+b2
解:a2+ab+ab+b2=(a+b)2.
2.(例1)计算:
(1)(x+3)2=x2+2·x·3+32=__________;
(2)(x-5)2=________________=__________.
x2-10x+25
x2+6x+9
x2-2·x·5+52
3. 计算:
(1)(x+1)2=________________=__________;
(2)(x-4)2=________________=__________.
x2-8x+16
x2+2·x·1+12
x2+2x+1
x2-2·x·4+42
4.(例2)计算:
(1)(3x+5y)2;
解:原式=(3x)2+2·3x·5y+(5y)2
=9x2+30xy+25y2
解:原式=(2x)2-2·2x·
=4x2-2x+
5. 计算:
(1)(4x-3y)2;
解:原式=(4x)2-2·4x·3y+(3y)2
=16x2-24xy+9y2
解:原式
6.(例3)计算:
(1)(-x+5)2;
(2)(-2x-y)2.
解: 原式=(-x)2+2·(-x)·5+52
=x2-10x+25
解:原式=(-2x)2-2·(-2x)·y+y2
=4x2+4xy+y2
7. 计算:
(1)(-x-3)2;
(2)(-m+3n)2.
解:原式=(-x)2-2·(-x)·3+32
=x2+6x+9
解:原式=(-m)2+2·(-m)·3n+(3n)2
=m2-6mn+9n2
知识点2:多项式乘以多项式的综合计算
8.(例4)计算:(x+5)2-(x-2)(x+3).
解:原式=x2+10x+25-(x2+x-6)
=x2+10x+25-x2-x+6
=9x+31
9. 计算:(2x+y)(2x-y)-(2x+y)2.
解:原式=4x2-y2-(4x2+4xy+y2)
=4x2-y2-4x2-4xy-y2
=-4xy-2y2
三、过关检测
第1关
10. 计算(a-2)2的结果是( )
A. a2-4a+4
B. a2-2a+4
C. a2-4
D. a2-4a-4
A
11. 若(x+3)2=x2-ax+9,则a的值是( )
A. 3 B. -3 C. 6 D. -6
D
12. 下列计算正确的是( )
A. (a+3)2=a2+9
B. (x-1)2=x2-1
C. (x-2)(x+3)=x2-6
D. (x+1)(x-1)=x2-1
D
13. 计算:
(1)(3x+2)2= ;
(2)(mn-3)2= ;
(3)( x-2y)2= .
9x2+12x+4
m2n2-6mn+9
x2-2xy+4y2
14. 计算:
(1)(n+4)2-n2;
(2)(-2a+1)2.
解:原式=n2+8n+16-n2
=8n+16
解:原式=(-2a)2+2·(-2a)+12
=4a2-4a+1
15. 运用完全平方公式进行简便运算:
(1)1022; (2)1972.
解:原式=(100+2)2
=1002+2×100×2+22
=10 000+400+4
=10 404
解:原式=(200-3)2
=2002-2×200×3+32
=40 000-1 200+9
=38 809
第2关
16. 化简求值:(x+2)2+(2x+1)(2x-1)-4x(x+1),其中,x=-2.
解:原式=(x2+4x+4)+(4x2-1)-(4x2+4x)
=x2+4x+4+4x2-1-4x2-4x
=x2+3
当x=-2时,原式=(-2)2+3=7
17.如图,根据图形的面积关系可以验证的公式是( )
A. (a-b)(a+b)=a2-b2
B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2
D. a2-b2=(a-b)(a+b)
C
第3关
18. 一个圆的半径长为r(r>2) cm,减少2 cm后,这个圆的面积减少了多少?
解:∵圆的半径长为r(r>2) cm,减少2 cm后的半径变为
(r-2) cm.
则半径减少后圆的面积为:
π(r-2)2=π(r2-4r+4)=πr2-4πr+4π.
∴圆的面积减少了:πr2-(πr2-4πr+4π)=(4πr-4π) cm2.
19.如图的三角形可解释(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
其中(a+b)0=1,
(a+b)1=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
根据“杨辉三角”计算(a+b)4.
解:原式=a4+4a3b+6a2b2+4ab3+b4
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
