第29章直线与圆的位置关系章节复习与小结-冀教版九年级数学下册课件(共20张ppt)
文档属性
| 名称 | 第29章直线与圆的位置关系章节复习与小结-冀教版九年级数学下册课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 11:43:59 | ||
图片预览






文档简介
复习与小结
第二十九章 直线与圆的位置关系
冀教版九下
学习目标
1.会用d与r的数量关系确定点、直线与圆的位置关系.
2.灵活运用切线的判定、性质解决问题.
3.会进行正多边形中的相关计算.
冀教版九下
知识回顾
一、点与圆的位置关系
1.d:
2.利用d与r的数量关系确定点与圆的位置关系
圆心到点的距离
r:
圆的半径
点在圆内
d点在圆上
d=r
点在圆外
d>r
要判断一个点和一个圆的位置关系,要先确定问题中的d和r,通过d和r的大小比较,得出点与圆的位置关系.
知识回顾
二、直线与圆的位置关系
1.d:
圆心到直线的距离
r:
圆的半径
2.利用d与r的数量关系确定直线与圆的位置关系
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
要判断直线和圆的位置关系,要先确定问题中的d和r,通过d和r的大小比较,得出直线与圆的位置关系.
知识运用
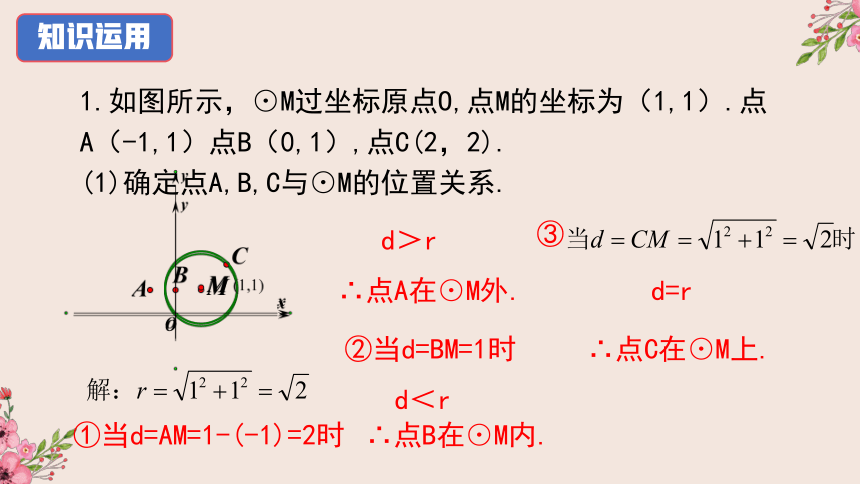
1.如图所示,⊙M过坐标原点O,点M的坐标为(1,1).点A(-1,1)点B(0,1),点C(2,2).
(1)确定点A,B,C与⊙M的位置关系.
①当d=AM=1-(-1)=2时
∴点A在⊙M外.
②当d=BM=1时
d>r
d<r
∴点B在⊙M内.
③
d=r
∴点C在⊙M上.
知识回顾
三、切线的判定与性质
1.切线的判定
①直线与圆有唯一公共点时,直线与圆相切.
②d=r时,直线与圆相切.
③直线经过半径的外端且与半径垂直时,直线与圆相切.
知识回顾
①直线与圆相切时,直线与圆有且只有一个公共点.
2.切线的性质
②直线与圆相切时,d=r.
③直线与圆相切时,直线垂直于过切点的半径.
三、切线的判定与性质
知识运用
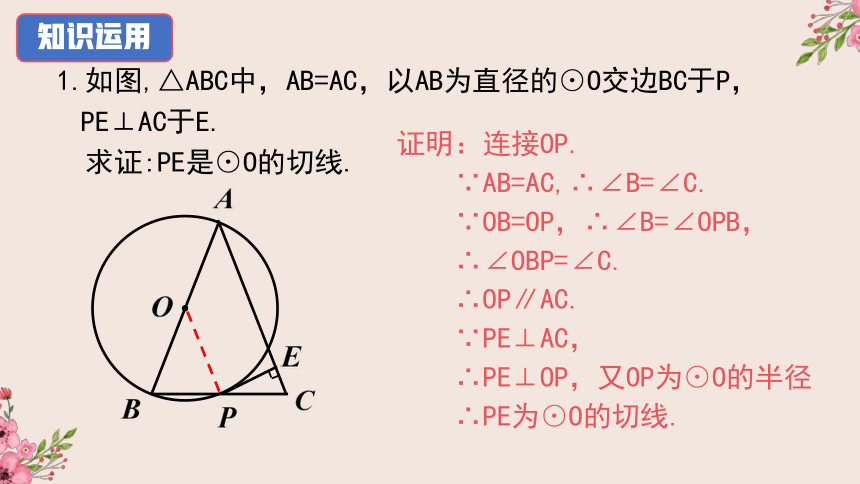
1.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
O
A
B
C
E
P
证明:连接OP.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP,又OP为⊙O的半径
∴PE为⊙O的切线.
知识运用
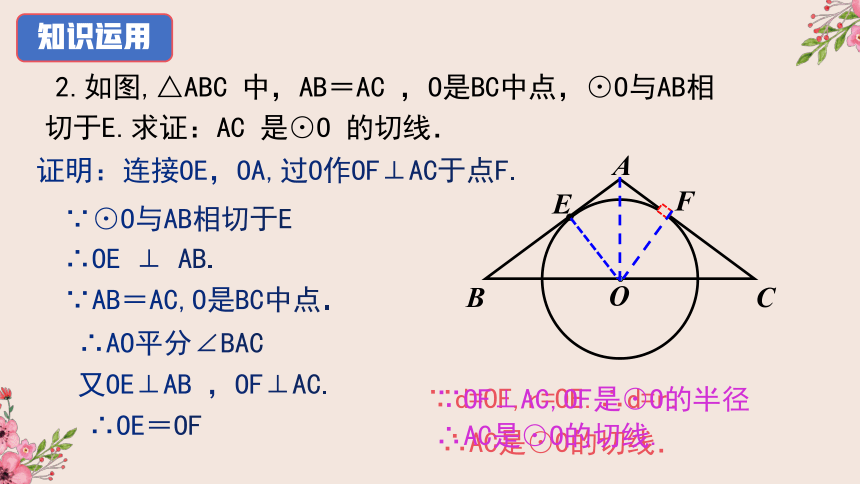
2.如图,△ABC 中,AB=AC ,O是BC中点,⊙O与AB相切于E.求证:AC 是⊙O 的切线.
B
O
C
E
A
F
证明:连接OE,OA,过O作OF⊥AC于点F.
∵⊙O与AB相切于E
∴OE ⊥ AB.
∵AB=AC,O是BC中点.
∴AO平分∠BAC
又OE⊥AB ,OF⊥AC.
∴OE=OF
∵d=OF,r=OE.∴d=r.
∴AC是⊙O的切线.
∵OF⊥AC,OF是⊙O的半径
∴AC是⊙O的切线.
知识回顾
四、切线长定理
1.切线长定理
过圆外一点所画的圆的两条切线的切线长相等.
用途:
得到相等的线段.
知识回顾
2.三角形的内切圆
①三角形的内心:
三角形的三个内角的平分线的交点.
四、切线长定理
到三角形三边的距离相等.
②直角三角形的内切圆半径:
知识运用
20 °
4
110 °
1.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4,∠APB= 40 ° ,∠APO= ,PB= .
B
P
O
A
第1题
2.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .
A
B
C
O
第2题
外心
80°
知识运用
3.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= .
65 °或115 °
B
P
O
A
第3题
4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
A
B
C
F
E
D
O
第4题
30
知识运用
5.如图,点I是△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为______.
A
B
C
I
4
知识回顾
五、正多边形和圆
1.正多边形的概念:
各边相等,各角也相等的多边形叫做正多边形.
中心、半径、中心角、边心距
2.正多边形中的相关概念:
知识回顾
五、正多边形和圆
3.正多边形中的计算题
边心距
半径
边的一半
中心角的一半
知识运用
2. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径,即正方形的对角线.
1.一个圆的内接正三角形的面积为 ,则此圆的内接正六边形的周长=_____.
48
知识运用
3.如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=________;
图②中∠MON= ;
图③中∠MON= ;
A
B
C
D
E
A
B
C
D
.
A
B
C
M
N
M
N
M
N
O
O
O
90 °
72 °
120 °
图①
图②
图③
知识运用
3.如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(2)试探究∠MON的度数与正n边形的边数n的关系.
A
B
C
D
E
M
N
O
图③
BM=CN,∠MBO=∠NCO,OB=OC
∠MON=∠BOC
∠MOB=∠NOC
∠BON=∠BON
△OMB≌△ONC
分析:
思考:四边形MONB的面积与正n边形的面积有什么关系?
同学们再见
第二十九章 直线与圆的位置关系
冀教版九下
学习目标
1.会用d与r的数量关系确定点、直线与圆的位置关系.
2.灵活运用切线的判定、性质解决问题.
3.会进行正多边形中的相关计算.
冀教版九下
知识回顾
一、点与圆的位置关系
1.d:
2.利用d与r的数量关系确定点与圆的位置关系
圆心到点的距离
r:
圆的半径
点在圆内
d
d=r
点在圆外
d>r
要判断一个点和一个圆的位置关系,要先确定问题中的d和r,通过d和r的大小比较,得出点与圆的位置关系.
知识回顾
二、直线与圆的位置关系
1.d:
圆心到直线的距离
r:
圆的半径
2.利用d与r的数量关系确定直线与圆的位置关系
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
要判断直线和圆的位置关系,要先确定问题中的d和r,通过d和r的大小比较,得出直线与圆的位置关系.
知识运用
1.如图所示,⊙M过坐标原点O,点M的坐标为(1,1).点A(-1,1)点B(0,1),点C(2,2).
(1)确定点A,B,C与⊙M的位置关系.
①当d=AM=1-(-1)=2时
∴点A在⊙M外.
②当d=BM=1时
d>r
d<r
∴点B在⊙M内.
③
d=r
∴点C在⊙M上.
知识回顾
三、切线的判定与性质
1.切线的判定
①直线与圆有唯一公共点时,直线与圆相切.
②d=r时,直线与圆相切.
③直线经过半径的外端且与半径垂直时,直线与圆相切.
知识回顾
①直线与圆相切时,直线与圆有且只有一个公共点.
2.切线的性质
②直线与圆相切时,d=r.
③直线与圆相切时,直线垂直于过切点的半径.
三、切线的判定与性质
知识运用
1.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
O
A
B
C
E
P
证明:连接OP.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP,又OP为⊙O的半径
∴PE为⊙O的切线.
知识运用
2.如图,△ABC 中,AB=AC ,O是BC中点,⊙O与AB相切于E.求证:AC 是⊙O 的切线.
B
O
C
E
A
F
证明:连接OE,OA,过O作OF⊥AC于点F.
∵⊙O与AB相切于E
∴OE ⊥ AB.
∵AB=AC,O是BC中点.
∴AO平分∠BAC
又OE⊥AB ,OF⊥AC.
∴OE=OF
∵d=OF,r=OE.∴d=r.
∴AC是⊙O的切线.
∵OF⊥AC,OF是⊙O的半径
∴AC是⊙O的切线.
知识回顾
四、切线长定理
1.切线长定理
过圆外一点所画的圆的两条切线的切线长相等.
用途:
得到相等的线段.
知识回顾
2.三角形的内切圆
①三角形的内心:
三角形的三个内角的平分线的交点.
四、切线长定理
到三角形三边的距离相等.
②直角三角形的内切圆半径:
知识运用
20 °
4
110 °
1.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4,∠APB= 40 ° ,∠APO= ,PB= .
B
P
O
A
第1题
2.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .
A
B
C
O
第2题
外心
80°
知识运用
3.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= .
65 °或115 °
B
P
O
A
第3题
4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
A
B
C
F
E
D
O
第4题
30
知识运用
5.如图,点I是△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为______.
A
B
C
I
4
知识回顾
五、正多边形和圆
1.正多边形的概念:
各边相等,各角也相等的多边形叫做正多边形.
中心、半径、中心角、边心距
2.正多边形中的相关概念:
知识回顾
五、正多边形和圆
3.正多边形中的计算题
边心距
半径
边的一半
中心角的一半
知识运用
2. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径,即正方形的对角线.
1.一个圆的内接正三角形的面积为 ,则此圆的内接正六边形的周长=_____.
48
知识运用
3.如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=________;
图②中∠MON= ;
图③中∠MON= ;
A
B
C
D
E
A
B
C
D
.
A
B
C
M
N
M
N
M
N
O
O
O
90 °
72 °
120 °
图①
图②
图③
知识运用
3.如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(2)试探究∠MON的度数与正n边形的边数n的关系.
A
B
C
D
E
M
N
O
图③
BM=CN,∠MBO=∠NCO,OB=OC
∠MON=∠BOC
∠MOB=∠NOC
∠BON=∠BON
△OMB≌△ONC
分析:
思考:四边形MONB的面积与正n边形的面积有什么关系?
同学们再见
