第30章二次函数复习与小结-冀教版九年级数学下册课件(共22张ppt)
文档属性
| 名称 | 第30章二次函数复习与小结-冀教版九年级数学下册课件(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 11:44:02 | ||
图片预览








文档简介
复习与小结
第三十章 二次函数
冀教版九下
整理知识点
一、二次函数的定义
1.一般地,如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.
当b=0时,抛物线为y=ax2+c,对称轴为y轴.
当c=0时,抛物线为y=ax2+bx,过原点.
当b=0,c=0时,抛物线为y=ax2,顶点为原点.
注意:
整理知识点
2.二次函数的三种基本形式
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a≠0),由顶点式可以直接写出二次函数的顶点坐标是(h,k);
(3)交点式:y=a(x-x1)(x-x2)(a≠0),其中x1,x2是图像与x轴交点的横坐标.
整理知识点
二、用待定系数法求二次函数表达式
1.若已知条件是图像上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
2.若已知二次函数的顶点坐标或对称轴,则设顶点式y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将解析式化为一般式.
3.若已知二次函数图像与x轴的两个交点的坐标,则设交点式y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数a的值,最后将解析式化为一般式.
巩固练习
1.已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
设为一般式
解:设所求的二次函数为y=ax2+bx+c, 由题意得:
解得, a=2,b=-3,c=5.
∴ 所求的二次函数为y=2x2-3x+5.
巩固练习
2.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.
解: ?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
设为顶点式
整理知识点
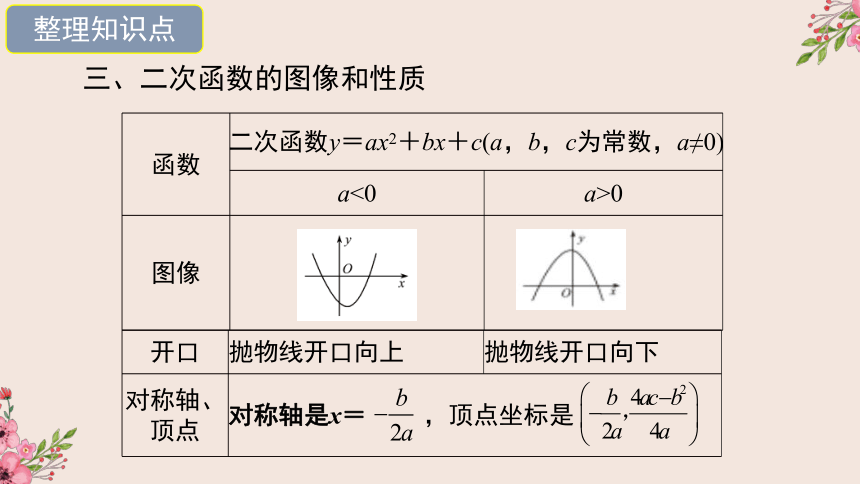
三、二次函数的图像和性质
{5940675A-B579-460E-94D1-54222C63F5DA}函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
a<0
a>0
图像
{5940675A-B579-460E-94D1-54222C63F5DA}开口
抛物线开口向上
抛物线开口向下
对称轴、顶点
对称轴是x= ,顶点坐标是
整理知识点
{5940675A-B579-460E-94D1-54222C63F5DA}增
减
性
在对称轴的左侧,即当x< 时,y随x的增大而减小;在对称轴的右侧,即当x> 时,y随x的增大而增大,简记为“左减右增”
在对称轴的左侧,即当x< 时,y随x的增大而增大;在对称轴的右侧,即当x> 时,y随x的增大而减小,简记为“左增右减”
最
值
抛物线有最低点,当
x= 时, y有最小值,
y最小值=
抛物线有最高点,当
x= 时,y有最大值,
y最大值=
巩固练习
1. 抛物线y=x2-2x+3的顶点坐标________.
解析:
方法一:配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二:代入顶点坐标公式 .
则顶点坐标为(1,2).
巩固练习
2.对于y=2(x-3)2+2的图像下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
C
巩固练习
3.下列函数中,当x>0时,y值随x值增大而减小的是( )
A. y= B.y=x-1 C. D.y=-3x2
D
4.二次函数y=-x2+bx+c的图像如图所示,若点A(x1,y1),B(x2,y2)在此函数
图像上,且x1 A. y1≤y2 B.y1 C.y1≥y2 D.y1>y2
B
整理知识点
四、二次函数y=ax2+bx+c的图像特征与系数a,b,c的关系
字母
字母的符号
图像的特征
a
a>0
开口向上
a<0
开口向下
b
b=0
对称轴为y轴
ab>0(a与b同号)
对称轴在y轴左侧
ab<0(a与b异号)
对称轴在y轴右侧
c
c=0
经过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
b2-4ac
b2-4ac=0
与x轴有唯一交点(顶点)
b2-4ac>0
与x轴有两个交点
b2-4ac<0
与x轴没有交点
巩固练习
1.已知二次函数y=ax2+bx+c的图像如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是( )
A.1 B.2 C.3 D.4
D
巩固练习
2.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
整理知识点
五、二次函数图像的平移
任意抛物线y=a(x-h)2+k可以由抛物线y=ax2经过平移得到
左右平移
在括号内左加右减
上下平移
在括号外上加下减
巩固练习
1.将抛物线y=x2-6x+5向上平移 2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
抛物线平移的规律可总结如下口诀:
左加右减,上加下减.
整理知识点
2.若抛物线 y=-7(x+4)2-1平移得到 y=-7x2,则可能( )
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向下平移4个单位
B
整理知识点
六、二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图像和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图像和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图像和x轴交点
一元二次方程
ax2+bx+c=0的根
一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个不相等的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
巩固练习
1. 若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6 B.x1=1,x2=7
C.x1=1,x2=﹣7 D.x1=﹣1,x2=7
D
整理知识点
七、二次函数的应用
1.一般步骤:(1)找出问题中的变量和常量以及它们之间的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)应用二次函数的图像及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
2.利用二次函数的知识常解决以下几类问题:最大利润问题,求几何图形面积的最值问题,拱桥问题,运动型几何问题,方案设计问题等.
巩固练习
1. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)设矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
同学们再见
第三十章 二次函数
冀教版九下
整理知识点
一、二次函数的定义
1.一般地,如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.
当b=0时,抛物线为y=ax2+c,对称轴为y轴.
当c=0时,抛物线为y=ax2+bx,过原点.
当b=0,c=0时,抛物线为y=ax2,顶点为原点.
注意:
整理知识点
2.二次函数的三种基本形式
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a≠0),由顶点式可以直接写出二次函数的顶点坐标是(h,k);
(3)交点式:y=a(x-x1)(x-x2)(a≠0),其中x1,x2是图像与x轴交点的横坐标.
整理知识点
二、用待定系数法求二次函数表达式
1.若已知条件是图像上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.
2.若已知二次函数的顶点坐标或对称轴,则设顶点式y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将解析式化为一般式.
3.若已知二次函数图像与x轴的两个交点的坐标,则设交点式y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数a的值,最后将解析式化为一般式.
巩固练习
1.已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析式.
设为一般式
解:设所求的二次函数为y=ax2+bx+c, 由题意得:
解得, a=2,b=-3,c=5.
∴ 所求的二次函数为y=2x2-3x+5.
巩固练习
2.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.
解: ?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
设为顶点式
整理知识点
三、二次函数的图像和性质
{5940675A-B579-460E-94D1-54222C63F5DA}函数
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)
a<0
a>0
图像
{5940675A-B579-460E-94D1-54222C63F5DA}开口
抛物线开口向上
抛物线开口向下
对称轴、顶点
对称轴是x= ,顶点坐标是
整理知识点
{5940675A-B579-460E-94D1-54222C63F5DA}增
减
性
在对称轴的左侧,即当x< 时,y随x的增大而减小;在对称轴的右侧,即当x> 时,y随x的增大而增大,简记为“左减右增”
在对称轴的左侧,即当x< 时,y随x的增大而增大;在对称轴的右侧,即当x> 时,y随x的增大而减小,简记为“左增右减”
最
值
抛物线有最低点,当
x= 时, y有最小值,
y最小值=
抛物线有最高点,当
x= 时,y有最大值,
y最大值=
巩固练习
1. 抛物线y=x2-2x+3的顶点坐标________.
解析:
方法一:配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二:代入顶点坐标公式 .
则顶点坐标为(1,2).
巩固练习
2.对于y=2(x-3)2+2的图像下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
C
巩固练习
3.下列函数中,当x>0时,y值随x值增大而减小的是( )
A. y= B.y=x-1 C. D.y=-3x2
D
4.二次函数y=-x2+bx+c的图像如图所示,若点A(x1,y1),B(x2,y2)在此函数
图像上,且x1
B
整理知识点
四、二次函数y=ax2+bx+c的图像特征与系数a,b,c的关系
字母
字母的符号
图像的特征
a
a>0
开口向上
a<0
开口向下
b
b=0
对称轴为y轴
ab>0(a与b同号)
对称轴在y轴左侧
ab<0(a与b异号)
对称轴在y轴右侧
c
c=0
经过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
b2-4ac
b2-4ac=0
与x轴有唯一交点(顶点)
b2-4ac>0
与x轴有两个交点
b2-4ac<0
与x轴没有交点
巩固练习
1.已知二次函数y=ax2+bx+c的图像如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2. 其中正确的个数是( )
A.1 B.2 C.3 D.4
D
巩固练习
2.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
整理知识点
五、二次函数图像的平移
任意抛物线y=a(x-h)2+k可以由抛物线y=ax2经过平移得到
左右平移
在括号内左加右减
上下平移
在括号外上加下减
巩固练习
1.将抛物线y=x2-6x+5向上平移 2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
抛物线平移的规律可总结如下口诀:
左加右减,上加下减.
整理知识点
2.若抛物线 y=-7(x+4)2-1平移得到 y=-7x2,则可能( )
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向下平移4个单位
B
整理知识点
六、二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图像和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图像和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图像和x轴交点
一元二次方程
ax2+bx+c=0的根
一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个不相等的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
巩固练习
1. 若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6 B.x1=1,x2=7
C.x1=1,x2=﹣7 D.x1=﹣1,x2=7
D
整理知识点
七、二次函数的应用
1.一般步骤:(1)找出问题中的变量和常量以及它们之间的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)应用二次函数的图像及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
2.利用二次函数的知识常解决以下几类问题:最大利润问题,求几何图形面积的最值问题,拱桥问题,运动型几何问题,方案设计问题等.
巩固练习
1. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)设矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
同学们再见
