第31章随机事件的概率复习与小结-冀教版九年级数学下册课件(24张)
文档属性
| 名称 | 第31章随机事件的概率复习与小结-冀教版九年级数学下册课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 11:46:03 | ||
图片预览








文档简介
冀教版九下
小结与复习
第三十一章 随机事件的概率
学习目标
1.了解必然事件、不可能事件、随机事件;
2.能通过列表、画树状图等方法列出简单随机事件所有可能的结果,从而求出事件的概率;
3.知道通过大量的重复试验,可以用频率来估计概率.
冀教版九下
知识回顾
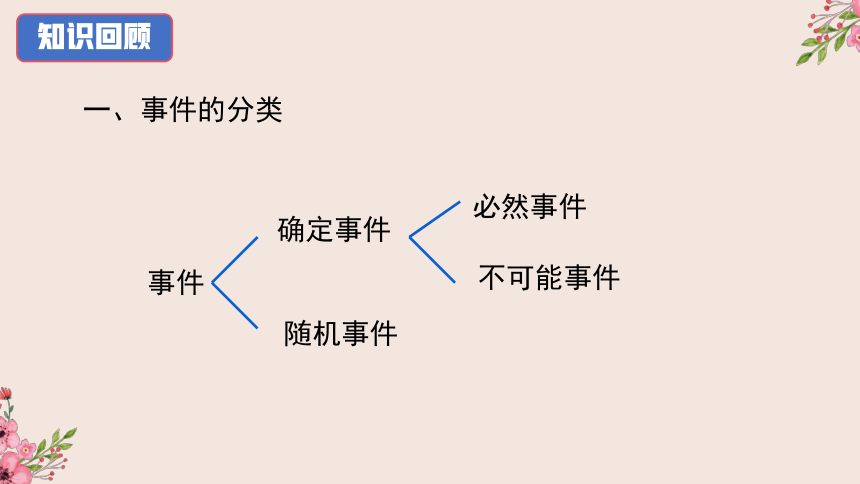
一、事件的分类
1.必然事件:在一定条件下必然发生的事件.
2.不可能事件:在一定条件下不可能发生的事件.
3.随机事件:在一定条件下可能发生也可能不发生的事件.
知识回顾
一、事件的分类
事件
随机事件
确定事件
必然事件
不可能事件
知识运用
C.画一个三角形,其内角和是180°是必然事件.
C
下列说法中正确的是( ).
B.袋中有10个蓝球,1个绿球,随机摸出一个球是蓝
球是必然事件.
A.射击运动员射击一次,命中靶心是必然事件.
D.经过有交通信号灯的路口,遇到红灯是必然事件.
知识回顾
二、事件的概率
我们用一个数刻画随机事件A发生的可能性大小,这个数叫做事件A的概率.一般地,如果一个试验中有n种等可能的结果,事件A包含其中m种结果,那么事件A发生的概率为P(A)=
知识回顾
1、必然事件的概率:
P(A)=1
二、事件的概率
2、不可能事件的概率:
P(A)=0
3、随机事件的概率:
0<P(A)<1
任何一个事件A的概率都满足0≤P(A)≤1
知识回顾
三、求随机事件的概率的方法
1. 直接公式法:如果一个试验有n种等可能的结果,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=____
2. 列表法:如果一次试验涉及两个因素,并且只有有限个等可能的结果,结果数目较多时,应列出所有可能的结果,通常采用列表法求事件发生的概率.
知识回顾
三、求随机事件的概率的方法
3. 画树状图法:当一次试验涉及三个或更多的因素时,通常采用画树状图法来求事件发生的概率
4. 频率估计概率:一般地,做n次重复试验,如果事件A发生了m次,比值稳定于某个常数P,那么事件A发生的概率:P(A)=P(0≤P(A)≤1)
5. 几何概型的概率公式:P(A)=
知识运用
B
1.在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其他差别,任意摸出一个红球的概率是( )
方法:
利用公式直接求
知识运用
2.文具店有三种品牌的6个笔记本,价格为4元、5元的各一个,价格为7元的有4个.若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本,嘉嘉先随机拿出一个本后不放回之后又随机从剩下的本中拿一个本,求嘉嘉两次都拿到7元本的概率.
分析:
由于结果的数目较多,因此可选择列表法.
知识运用
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
4
5
a
b
c
4
×
(4,5)
(4,a)
(4,b)
(4,c)
5
(5,4)
×
(5,a)
(5,b)
(5,c)
a
(a,4)
(a,5)
×
(a,b)
(a,c)
b
(b,4)
(b,5)
(b,a)
×
(b,c)
c
(c,4)
(c,5)
(c,a)
(c,b)
×
设4元本、5元本为4,5;7元本为a,b,c.
第一次
第二次
共有20种等可能的结果,其中两次都拿到7元本有6种.
不放回
知识运用
3.同时掷三枚质地均匀的硬币,落地后,求三枚都是正面向上的概率.
分析:
由于涉及3个因素,列表法不可用,且结果数目不多,可选择树形图.
知识运用
共有8种等可能的结果,其中三枚都是正面向上的有1种.
第一枚
第二枚
第三枚
1
1
2
1
2
1
2
2
1
2
1
2
1
2
结果
111
112
121
122
211
212
221
222
开始
知识运用
4.现有4条线段,长度依次为2,4,6,7,从中任选三条,能组成三角形的概率是_______.
分析:
由于涉及3个因素,不能选择列表法,若选择树形图,结果的数目较多,画起来比较乱,因此可选则直接列举法.
所有可能结果为:2 4 6 2 4 7 2 6 7 4 6 7共4种.
其中能组成三角形的有2种.
知识运用
5.大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码示意图,用打印机打印边长为2cm的正方形区域内,为了估计图中绿色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入绿色部分的频率稳定在0.6左右,据此可以估计绿色部分的总面积约为_________cm?.
考查知识点:
1.大量试验前提下,可用频率估计概率.
2.几何概率.
知识运用
解:∵经过大量重复试验,发现点落入绿色部分的频率稳定在0.6左右.
∴点落入绿色部分是概率为0.6.
∵边长为2cm的正方形的面积为4cm.
设绿色部分的面积为S.
解得,S=2.4.
∴估计绿色部分的总面积约2.4cm?.
感受中考
1. (2019河北22题9分)某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知P(一次拿到8元球)= .
(1)求这4个球价格的众数;
解:(1)∵P(一次拿到8元球)= ,
∴8元球为2个.
∴四个乒乓球的价格为7、8、8、9.
∴这四个球价格的众数为8;(3分)
感受中考
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
(2)①相同;(4分)
理由:原四个球的中位数为8,拿走一个7元球后,剩余球的价格为8、8、9,中位数为8,与原来4个球价格的中位数相同.(7分)
感受中考
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
{5940675A-B579-460E-94D1-54222C63F5DA} 又拿
先拿
8
8
9
8
(8,8)
(8,8)
(8,9)
8
(8,8)
(8,8)
(8,9)
9
(9,8)
(9,8)
(9,9)
共有9种等可能的结果,其中乙组两次都拿到8元球的结果共4种,(8分)
∴P(乙组两次都拿到8元球)= .(9分)
感受中考
2. (2020河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
感受中考
(1)依题意,得移动一次共有4种等可能的情况,只有甲对乙错时,甲才能停留在正半轴上,∴P(甲的位置停留在正半轴上)= ;
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;
(2)依题意,得m=5+(-4)n+2(10-n)=25-6n.
当表示乙的点离原点O最近时,|m|取最小值,此时n=4,
∴表示乙的点离原点最近时n的值为4;
感受中考
(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.
(3)k的值为3或5.
分析:设两人间的距离为s,若甲、乙两人都对或都错,两人间的距离s=8-2k(k≤4)或s=2k-8(k>4),当s=2时,k=3或k=5;若甲、乙两人所猜结果一对一错,当甲对、乙错时两人间的距离为s=(5+2k)-(-3+4k)=8-2k (k≤4)或s=(-3+4k)-(5+2k)=2k-8(k>4),当s=2时,k=3或k=5;当乙对、甲错时两人间的距离为s=(5-4k)-(-3-2k)=8-2k(k≤4)或s=(-3-2k)-(5-4k)=2k-8(k>4),当s=2时,k=3或k=5;综上所述,k的值为3或5.
同学们再见
小结与复习
第三十一章 随机事件的概率
学习目标
1.了解必然事件、不可能事件、随机事件;
2.能通过列表、画树状图等方法列出简单随机事件所有可能的结果,从而求出事件的概率;
3.知道通过大量的重复试验,可以用频率来估计概率.
冀教版九下
知识回顾
一、事件的分类
1.必然事件:在一定条件下必然发生的事件.
2.不可能事件:在一定条件下不可能发生的事件.
3.随机事件:在一定条件下可能发生也可能不发生的事件.
知识回顾
一、事件的分类
事件
随机事件
确定事件
必然事件
不可能事件
知识运用
C.画一个三角形,其内角和是180°是必然事件.
C
下列说法中正确的是( ).
B.袋中有10个蓝球,1个绿球,随机摸出一个球是蓝
球是必然事件.
A.射击运动员射击一次,命中靶心是必然事件.
D.经过有交通信号灯的路口,遇到红灯是必然事件.
知识回顾
二、事件的概率
我们用一个数刻画随机事件A发生的可能性大小,这个数叫做事件A的概率.一般地,如果一个试验中有n种等可能的结果,事件A包含其中m种结果,那么事件A发生的概率为P(A)=
知识回顾
1、必然事件的概率:
P(A)=1
二、事件的概率
2、不可能事件的概率:
P(A)=0
3、随机事件的概率:
0<P(A)<1
任何一个事件A的概率都满足0≤P(A)≤1
知识回顾
三、求随机事件的概率的方法
1. 直接公式法:如果一个试验有n种等可能的结果,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=____
2. 列表法:如果一次试验涉及两个因素,并且只有有限个等可能的结果,结果数目较多时,应列出所有可能的结果,通常采用列表法求事件发生的概率.
知识回顾
三、求随机事件的概率的方法
3. 画树状图法:当一次试验涉及三个或更多的因素时,通常采用画树状图法来求事件发生的概率
4. 频率估计概率:一般地,做n次重复试验,如果事件A发生了m次,比值稳定于某个常数P,那么事件A发生的概率:P(A)=P(0≤P(A)≤1)
5. 几何概型的概率公式:P(A)=
知识运用
B
1.在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其他差别,任意摸出一个红球的概率是( )
方法:
利用公式直接求
知识运用
2.文具店有三种品牌的6个笔记本,价格为4元、5元的各一个,价格为7元的有4个.若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本,嘉嘉先随机拿出一个本后不放回之后又随机从剩下的本中拿一个本,求嘉嘉两次都拿到7元本的概率.
分析:
由于结果的数目较多,因此可选择列表法.
知识运用
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
4
5
a
b
c
4
×
(4,5)
(4,a)
(4,b)
(4,c)
5
(5,4)
×
(5,a)
(5,b)
(5,c)
a
(a,4)
(a,5)
×
(a,b)
(a,c)
b
(b,4)
(b,5)
(b,a)
×
(b,c)
c
(c,4)
(c,5)
(c,a)
(c,b)
×
设4元本、5元本为4,5;7元本为a,b,c.
第一次
第二次
共有20种等可能的结果,其中两次都拿到7元本有6种.
不放回
知识运用
3.同时掷三枚质地均匀的硬币,落地后,求三枚都是正面向上的概率.
分析:
由于涉及3个因素,列表法不可用,且结果数目不多,可选择树形图.
知识运用
共有8种等可能的结果,其中三枚都是正面向上的有1种.
第一枚
第二枚
第三枚
1
1
2
1
2
1
2
2
1
2
1
2
1
2
结果
111
112
121
122
211
212
221
222
开始
知识运用
4.现有4条线段,长度依次为2,4,6,7,从中任选三条,能组成三角形的概率是_______.
分析:
由于涉及3个因素,不能选择列表法,若选择树形图,结果的数目较多,画起来比较乱,因此可选则直接列举法.
所有可能结果为:2 4 6 2 4 7 2 6 7 4 6 7共4种.
其中能组成三角形的有2种.
知识运用
5.大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码示意图,用打印机打印边长为2cm的正方形区域内,为了估计图中绿色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入绿色部分的频率稳定在0.6左右,据此可以估计绿色部分的总面积约为_________cm?.
考查知识点:
1.大量试验前提下,可用频率估计概率.
2.几何概率.
知识运用
解:∵经过大量重复试验,发现点落入绿色部分的频率稳定在0.6左右.
∴点落入绿色部分是概率为0.6.
∵边长为2cm的正方形的面积为4cm.
设绿色部分的面积为S.
解得,S=2.4.
∴估计绿色部分的总面积约2.4cm?.
感受中考
1. (2019河北22题9分)某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知P(一次拿到8元球)= .
(1)求这4个球价格的众数;
解:(1)∵P(一次拿到8元球)= ,
∴8元球为2个.
∴四个乒乓球的价格为7、8、8、9.
∴这四个球价格的众数为8;(3分)
感受中考
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
(2)①相同;(4分)
理由:原四个球的中位数为8,拿走一个7元球后,剩余球的价格为8、8、9,中位数为8,与原来4个球价格的中位数相同.(7分)
感受中考
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
{5940675A-B579-460E-94D1-54222C63F5DA} 又拿
先拿
8
8
9
8
(8,8)
(8,8)
(8,9)
8
(8,8)
(8,8)
(8,9)
9
(9,8)
(9,8)
(9,9)
共有9种等可能的结果,其中乙组两次都拿到8元球的结果共4种,(8分)
∴P(乙组两次都拿到8元球)= .(9分)
感受中考
2. (2020河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
感受中考
(1)依题意,得移动一次共有4种等可能的情况,只有甲对乙错时,甲才能停留在正半轴上,∴P(甲的位置停留在正半轴上)= ;
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;
(2)依题意,得m=5+(-4)n+2(10-n)=25-6n.
当表示乙的点离原点O最近时,|m|取最小值,此时n=4,
∴表示乙的点离原点最近时n的值为4;
感受中考
(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.
(3)k的值为3或5.
分析:设两人间的距离为s,若甲、乙两人都对或都错,两人间的距离s=8-2k(k≤4)或s=2k-8(k>4),当s=2时,k=3或k=5;若甲、乙两人所猜结果一对一错,当甲对、乙错时两人间的距离为s=(5+2k)-(-3+4k)=8-2k (k≤4)或s=(-3+4k)-(5+2k)=2k-8(k>4),当s=2时,k=3或k=5;当乙对、甲错时两人间的距离为s=(5-4k)-(-3-2k)=8-2k(k≤4)或s=(-3-2k)-(5-4k)=2k-8(k>4),当s=2时,k=3或k=5;综上所述,k的值为3或5.
同学们再见
