第32章投影与试图章节复习与小结-冀教版九年级数学下册课件(共20张ppt)
文档属性
| 名称 | 第32章投影与试图章节复习与小结-冀教版九年级数学下册课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览






文档简介
复 习 与 小 结
第三十二章 投影与试图
冀教版九下
学 习 目 标
冀教版九下
1.了解中心投影和平行投影的概念;
2.会画直棱柱、圆柱、圆锥、球的三视图,能判断简单物体的视图,并会根据视图描述简单的几何体;
3.了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作实物模型;
4.了解上述视图与展开图在现实生活中的应用.
知识回顾
一、平行投影和中心投影
由 形成的投影是平行投影.
由 形成的投影叫做中心投影.
投影线 投影面产生的投影叫做正投影.
平行光线
同一点发出的光线
垂直于
注意:
1.平行投影中,光线平行,影子平行.
2.在中心投影中,光源与物体顶端的连线、光源与底面的垂直点与物体底端的连线相交于一点.
知识运用
1.下列语句正确的有_________.
①同一地区同一时刻的物体在阳光照射下,影子的方向是相同的;
②物体在任何光线照射下的影子的方向都是相同的;
③物体在路灯的照射下,影子方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
①③
知识运用
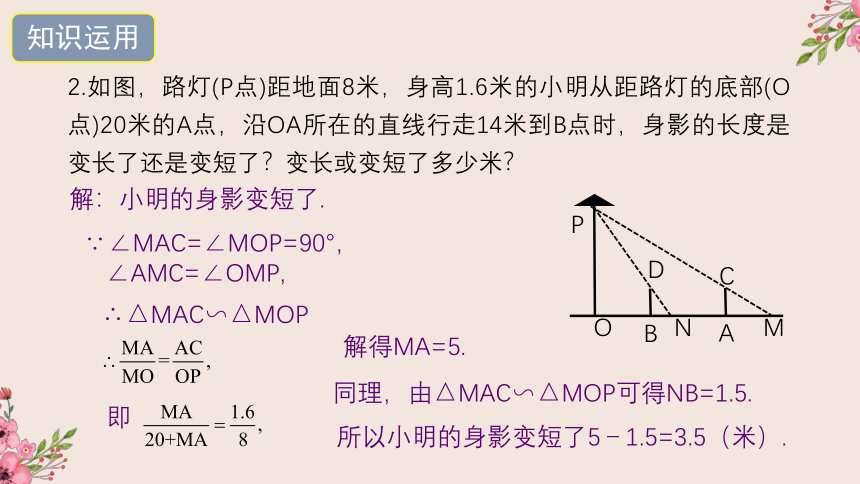
2.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解:小明的身影变短了.
∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP
即
解得MA=5.
同理,由△MAC∽△MOP可得NB=1.5.
所以小明的身影变短了5-1.5=3.5(米).
P
O
N
M
D
C
B
A
知识回顾
1.三视图的概念
主视图:在正面内得到的自前向后观察物体的视图
左视图:在侧面内得到的自左向右观察物体的视图
俯视图:在水平面内得到的自上向下观察物体的视图
二、三视图
2.三视图的摆放位置
俯视图在主视图的下面,左视图在主视图的右面.
知识回顾
3.三视图的画法
1.作水平投影:主视图与俯视图的_________.主视图与左视图的___________左视图与俯视图的__________.
2.作轮廓线:看得见部分的轮廓线画成__________,因被其他部分遮挡而看不见部分的轮廓线画成_________
长对正
高平齐
宽相等
实线
虚线
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
三视图
几何体
三视图
知识回顾
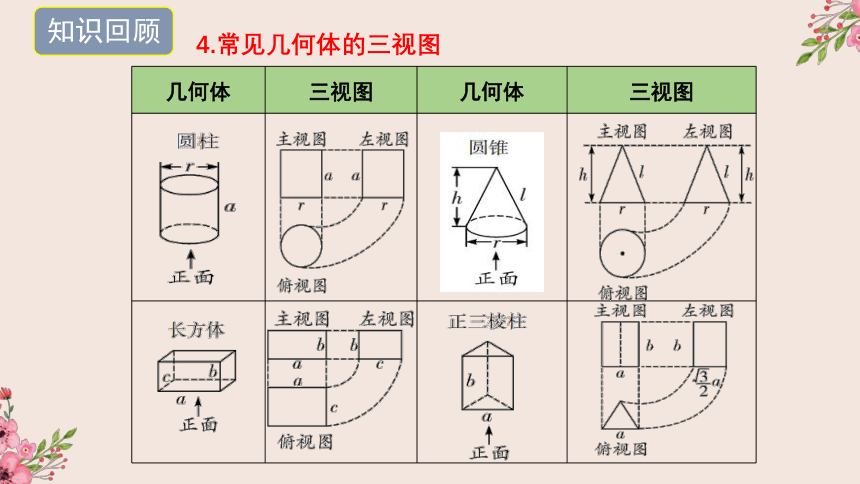
4.常见几何体的三视图
知识运用
A
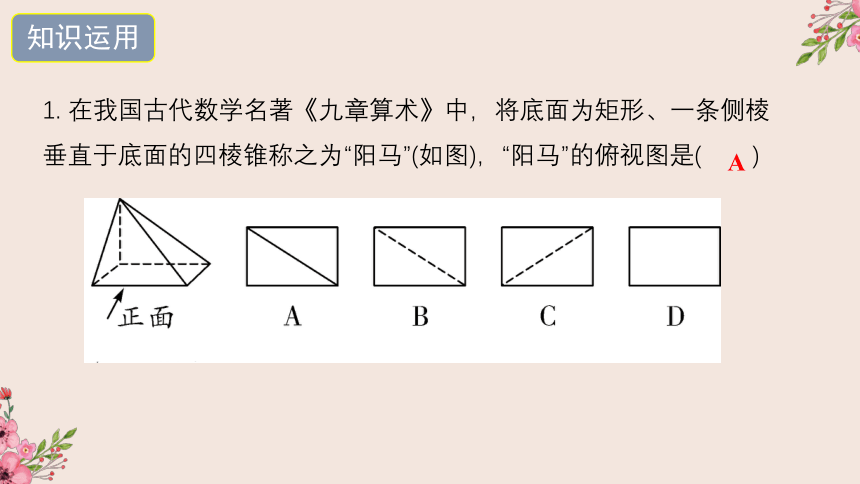
1. 在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图),“阳马”的俯视图是( )
知识运用
2.已知一个几何体的三视图如图所示,则该几何体是( )
A.棱柱 B.圆柱 C.圆锥 D.球
B
知识运用
3.已知一个几何体的三视图如图所示,则该几何体的表面积为( )
A.15π B.51π C.66π D.24π
●
4
8
D
1.立体图形的折叠:一个几何体能展开成一个平面图形,这个平面图形就可以折叠成相应的几何体,展开与折叠是一个互逆过程.
3.最短路径问题:先把立体图形展开成平面图形,根据“两点之间,线段最短”原则,在平面图形上构造直角三角形解决此类问题
知识回顾
三、立体图形的展开和折叠
2.常见的立体图形的侧面展开图:
圆锥的侧面展开图是一个扇形
直棱柱的侧面展开图是矩形
4.常见立体图形的表面展开图
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
立体图
表面展开图
侧面展开图
圆柱
圆锥
直三棱柱
知识回顾
1.图①是边长为1的六个小正方形组成的图形,它可以围成图②的正方体,则图①中小正方形顶点A,B在围成的正方体上的距离是( )
A. 0 B. 1 C. D.
B
知识运用
2.如图,圆锥的母线长为3,底面半径为1,A为底面圆周上一点,从点A出发绕侧面到点B(母线的中点)的最短路线长为_______.
知识运用
3. 我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为( )
A. 16+16 B. 16+8 C. 24+16 D. 4+4
A
知识运用
知识运用
4.某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
100
50
50
100
分析:在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
解:由三视图可知,密封罐的形状是正六棱柱.
密封罐的高为50mm,店面正六边形的直径为100mm,边长为50mm,右图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
(mm2)
知识运用
课堂小结
中心投影
视图与投影
视图
投影
平行投影
灯光与影子
圆柱、圆锥、球、直棱柱等简单几何体的三视图
正投影
直棱柱、圆锥的侧面展开图
同学们再见
第三十二章 投影与试图
冀教版九下
学 习 目 标
冀教版九下
1.了解中心投影和平行投影的概念;
2.会画直棱柱、圆柱、圆锥、球的三视图,能判断简单物体的视图,并会根据视图描述简单的几何体;
3.了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作实物模型;
4.了解上述视图与展开图在现实生活中的应用.
知识回顾
一、平行投影和中心投影
由 形成的投影是平行投影.
由 形成的投影叫做中心投影.
投影线 投影面产生的投影叫做正投影.
平行光线
同一点发出的光线
垂直于
注意:
1.平行投影中,光线平行,影子平行.
2.在中心投影中,光源与物体顶端的连线、光源与底面的垂直点与物体底端的连线相交于一点.
知识运用
1.下列语句正确的有_________.
①同一地区同一时刻的物体在阳光照射下,影子的方向是相同的;
②物体在任何光线照射下的影子的方向都是相同的;
③物体在路灯的照射下,影子方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
①③
知识运用
2.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解:小明的身影变短了.
∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP
即
解得MA=5.
同理,由△MAC∽△MOP可得NB=1.5.
所以小明的身影变短了5-1.5=3.5(米).
P
O
N
M
D
C
B
A
知识回顾
1.三视图的概念
主视图:在正面内得到的自前向后观察物体的视图
左视图:在侧面内得到的自左向右观察物体的视图
俯视图:在水平面内得到的自上向下观察物体的视图
二、三视图
2.三视图的摆放位置
俯视图在主视图的下面,左视图在主视图的右面.
知识回顾
3.三视图的画法
1.作水平投影:主视图与俯视图的_________.主视图与左视图的___________左视图与俯视图的__________.
2.作轮廓线:看得见部分的轮廓线画成__________,因被其他部分遮挡而看不见部分的轮廓线画成_________
长对正
高平齐
宽相等
实线
虚线
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
三视图
几何体
三视图
知识回顾
4.常见几何体的三视图
知识运用
A
1. 在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图),“阳马”的俯视图是( )
知识运用
2.已知一个几何体的三视图如图所示,则该几何体是( )
A.棱柱 B.圆柱 C.圆锥 D.球
B
知识运用
3.已知一个几何体的三视图如图所示,则该几何体的表面积为( )
A.15π B.51π C.66π D.24π
●
4
8
D
1.立体图形的折叠:一个几何体能展开成一个平面图形,这个平面图形就可以折叠成相应的几何体,展开与折叠是一个互逆过程.
3.最短路径问题:先把立体图形展开成平面图形,根据“两点之间,线段最短”原则,在平面图形上构造直角三角形解决此类问题
知识回顾
三、立体图形的展开和折叠
2.常见的立体图形的侧面展开图:
圆锥的侧面展开图是一个扇形
直棱柱的侧面展开图是矩形
4.常见立体图形的表面展开图
{5940675A-B579-460E-94D1-54222C63F5DA}几何体
立体图
表面展开图
侧面展开图
圆柱
圆锥
直三棱柱
知识回顾
1.图①是边长为1的六个小正方形组成的图形,它可以围成图②的正方体,则图①中小正方形顶点A,B在围成的正方体上的距离是( )
A. 0 B. 1 C. D.
B
知识运用
2.如图,圆锥的母线长为3,底面半径为1,A为底面圆周上一点,从点A出发绕侧面到点B(母线的中点)的最短路线长为_______.
知识运用
3. 我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为( )
A. 16+16 B. 16+8 C. 24+16 D. 4+4
A
知识运用
知识运用
4.某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
100
50
50
100
分析:在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
解:由三视图可知,密封罐的形状是正六棱柱.
密封罐的高为50mm,店面正六边形的直径为100mm,边长为50mm,右图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
(mm2)
知识运用
课堂小结
中心投影
视图与投影
视图
投影
平行投影
灯光与影子
圆柱、圆锥、球、直棱柱等简单几何体的三视图
正投影
直棱柱、圆锥的侧面展开图
同学们再见
