沪教版(上海)数学八年级第二学期-20章小结 一次函数的复习 课件(共18张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-20章小结 一次函数的复习 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览






文档简介
一次函数的复习
要点回顾
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
当k=0时,函数y=b(b是常数)叫做______函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
k≠0
2、一次函数y=kx+b(k≠0)的图象是过点
(0,___),(____,0)的__________。
b
一条直线
常值
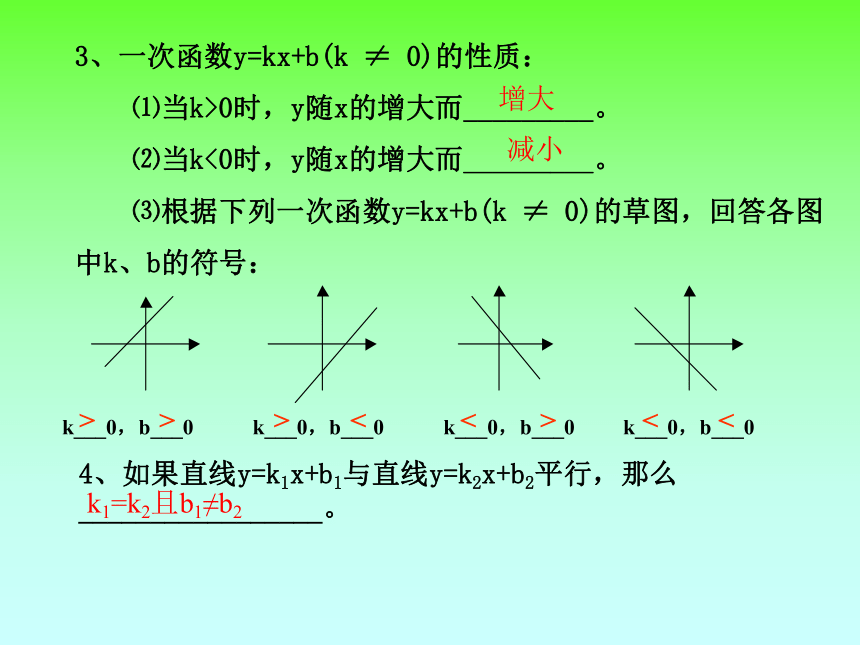
3、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图,回答各图
中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
增大
减小
4、如果直线y=k1x+b1与直线y=k2x+b2平行,那么
_________________。
k1=k2且b1≠b2
基础训练
1、把直线y=-3x沿y轴向________平移________个
单位得到直线y=-3x-2 。
2.直线y=-4x+5是由直线y=-4x+1沿y轴向________
平移________个单位得到的。
下
2
上
4
试一试:直线的平移
两直线平行, 相等;
直线沿y轴上下平移,看 )
(归纳:
斜率k
截距b
②
①、②、③
( -4, 0 )
y=2x+10
( 0, 4 )
③
练一练:
1、有下列函数:① , ② y=2x ,
③ , ④ 。其中过原点的直线
是_____;函数y随x的增大而增大的是___________;
图像在第一、二、三象限的是_____,它与x轴的交点坐标
是________ ,与y轴的交点坐标是_________ 。
3、直线y=kx+b与y=2x-5平行,并经过点(0,10),
则这个一次函数的解析式是______________ 。
2、已知点A(-1,a),B(3,b)在函数y=3x+ 4 的图像上,
则a与b的大小关系是( )
(A) a > b (B) a = b (C) a < b (D)不能比较
C
(看导学单:归纳求一次函数表达式的条件)
根据下列条件,求直线 的表达式:
4、直线 经过点A(1,-2)和B(-2,-3);
5、直线 经过点M(1,-2),它和x轴交点的
横坐标是-3;
6、直线 经过点(1,5),且它在y轴上的
截距是-3;
7、直线 与直线 平行,
它与y轴的交点到x轴的距离为2。
练一练:待定系数法
5. 函数y=f(x)的图像如图,这个函数的解析式是( )
(A) (B)
(C) (D)
D
解:设y=kx+2 经过点(3,0)
例1、如图一次函数与正比例函数的图像交于第三象限内的点A,与y轴交于点B(0,-4),且AO=AB,△AOB的面积为6,
求两函数解析式。
x
y
O
A
B(0,-4)
C
2
解:作AC⊥x轴,垂足是点C
∵AO=AB,B(0,-4)
又∵
∴AC=3
∴A(-3,-2)
∴OC=BC=2
x
O
A
B(0,-4)
C
2
3
(-3,-2)
y
例1、一次函数与正比例函数的图像交于第三象限内的点A,与y轴交于点B(0,-4),且AO=AB,△AOB的面积为6. 求两函数解析式。
归纳:
在求一次函数表达式时,
只要在k、b、直线上点的坐标或三角形面积等条件中,给定两个独立条件,就可求出它的表达式.
7.求直线y=2x+3、y=-2x-1与y轴围成的
三角形的面积
若将题中的y轴改为x轴,
你会做吗?
x
y
O
y=2x+3
y=-2x-1
A
B
C
D
P
练一练
7、已知一次函数y=kx+b的图像如图,
那么方程kx+b=0的解是 ,
不等式kx+b<0的解集为 .
X=2
X<2
归纳:
一次函数与一元一次方程、一元一次不等式的联系
(想一想:还有其他解法吗?)
先求出函数表达式 y=x-2
当y=0时,x-2=0,解得x=2
1、某植物栽t天后的高度为ycm,图中反映了y与t之间的关系,根据图象回答下列问题:
(1)植物刚栽的时候多高?
9
6
3
12
15
18
21
24
2
4
6
8
10
12
14
t/天
Y cm
(2)3天后该植物高度为多少?
(3)几天后该植物高度可达21cm?
(4)先写出y与t的关系式,
再计算长到100cm需几天?
(注意:数形结合思想)
一次函数的应用
关系式y=t+9
当y=100cm时,t=91(天)
2、 某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李重量x千克的关系如图:
⑴ 旅客最多可免费携带多少千克行李?
⑵超过30千克后,每千克需付多少元?
想一想:
红色那段图像表示什么意思?
生活中的数学
做 一 做
?
(3)求y关于x的函数表达式
小结:
1、通过学习,我们理解了一次函数的概念,认识和研究了函数的图像和性质,学会了一次函数的实际应用,并通过一次函数的图像揭示一元一次方程的根与一元一次不等式的解集的联系。
2、在运用待定系数法,求一次函数解析式时,只要在k、b、直线上点的坐标或面积等条件中,给定两个独立条件,或根据图像,就可求出它的表达式.
3、要 善于捕捉图像中的所有信息,并能够熟练地转化成实际问题。
鉴赏与评析
要点回顾
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
当k=0时,函数y=b(b是常数)叫做______函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
k≠0
2、一次函数y=kx+b(k≠0)的图象是过点
(0,___),(____,0)的__________。
b
一条直线
常值
3、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图,回答各图
中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
增大
减小
4、如果直线y=k1x+b1与直线y=k2x+b2平行,那么
_________________。
k1=k2且b1≠b2
基础训练
1、把直线y=-3x沿y轴向________平移________个
单位得到直线y=-3x-2 。
2.直线y=-4x+5是由直线y=-4x+1沿y轴向________
平移________个单位得到的。
下
2
上
4
试一试:直线的平移
两直线平行, 相等;
直线沿y轴上下平移,看 )
(归纳:
斜率k
截距b
②
①、②、③
( -4, 0 )
y=2x+10
( 0, 4 )
③
练一练:
1、有下列函数:① , ② y=2x ,
③ , ④ 。其中过原点的直线
是_____;函数y随x的增大而增大的是___________;
图像在第一、二、三象限的是_____,它与x轴的交点坐标
是________ ,与y轴的交点坐标是_________ 。
3、直线y=kx+b与y=2x-5平行,并经过点(0,10),
则这个一次函数的解析式是______________ 。
2、已知点A(-1,a),B(3,b)在函数y=3x+ 4 的图像上,
则a与b的大小关系是( )
(A) a > b (B) a = b (C) a < b (D)不能比较
C
(看导学单:归纳求一次函数表达式的条件)
根据下列条件,求直线 的表达式:
4、直线 经过点A(1,-2)和B(-2,-3);
5、直线 经过点M(1,-2),它和x轴交点的
横坐标是-3;
6、直线 经过点(1,5),且它在y轴上的
截距是-3;
7、直线 与直线 平行,
它与y轴的交点到x轴的距离为2。
练一练:待定系数法
5. 函数y=f(x)的图像如图,这个函数的解析式是( )
(A) (B)
(C) (D)
D
解:设y=kx+2 经过点(3,0)
例1、如图一次函数与正比例函数的图像交于第三象限内的点A,与y轴交于点B(0,-4),且AO=AB,△AOB的面积为6,
求两函数解析式。
x
y
O
A
B(0,-4)
C
2
解:作AC⊥x轴,垂足是点C
∵AO=AB,B(0,-4)
又∵
∴AC=3
∴A(-3,-2)
∴OC=BC=2
x
O
A
B(0,-4)
C
2
3
(-3,-2)
y
例1、一次函数与正比例函数的图像交于第三象限内的点A,与y轴交于点B(0,-4),且AO=AB,△AOB的面积为6. 求两函数解析式。
归纳:
在求一次函数表达式时,
只要在k、b、直线上点的坐标或三角形面积等条件中,给定两个独立条件,就可求出它的表达式.
7.求直线y=2x+3、y=-2x-1与y轴围成的
三角形的面积
若将题中的y轴改为x轴,
你会做吗?
x
y
O
y=2x+3
y=-2x-1
A
B
C
D
P
练一练
7、已知一次函数y=kx+b的图像如图,
那么方程kx+b=0的解是 ,
不等式kx+b<0的解集为 .
X=2
X<2
归纳:
一次函数与一元一次方程、一元一次不等式的联系
(想一想:还有其他解法吗?)
先求出函数表达式 y=x-2
当y=0时,x-2=0,解得x=2
1、某植物栽t天后的高度为ycm,图中反映了y与t之间的关系,根据图象回答下列问题:
(1)植物刚栽的时候多高?
9
6
3
12
15
18
21
24
2
4
6
8
10
12
14
t/天
Y cm
(2)3天后该植物高度为多少?
(3)几天后该植物高度可达21cm?
(4)先写出y与t的关系式,
再计算长到100cm需几天?
(注意:数形结合思想)
一次函数的应用
关系式y=t+9
当y=100cm时,t=91(天)
2、 某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李重量x千克的关系如图:
⑴ 旅客最多可免费携带多少千克行李?
⑵超过30千克后,每千克需付多少元?
想一想:
红色那段图像表示什么意思?
生活中的数学
做 一 做
?
(3)求y关于x的函数表达式
小结:
1、通过学习,我们理解了一次函数的概念,认识和研究了函数的图像和性质,学会了一次函数的实际应用,并通过一次函数的图像揭示一元一次方程的根与一元一次不等式的解集的联系。
2、在运用待定系数法,求一次函数解析式时,只要在k、b、直线上点的坐标或面积等条件中,给定两个独立条件,或根据图像,就可求出它的表达式.
3、要 善于捕捉图像中的所有信息,并能够熟练地转化成实际问题。
鉴赏与评析
