沪教版(上海)数学八年级第二学期-21.3 无理方程 课件(共19张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-21.3 无理方程 课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览






文档简介
21.4无理方程
问题引入
观察
所列的方程有什么特点?它与前面所学的方程有什么区别?
已知一个实数x(x>0)的3倍与4的和的算术平方根等于它本身,求实数x.
21.4无理方程
定义
方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程。无理方程也叫做根式方程。
辨一辨:下列方程是不是无理方程?若不是,则是什么方程?
(1)
(2)
(3)
整式方程
分式方程
无理方程
实数
有理数
无理数
整数
分数
有理式
无理式
代数式
整式
分式
代数方程
有理方程
无理方程
整式方程
分式方程
正整数
零
负整数
多项式
单项式
类比
定义
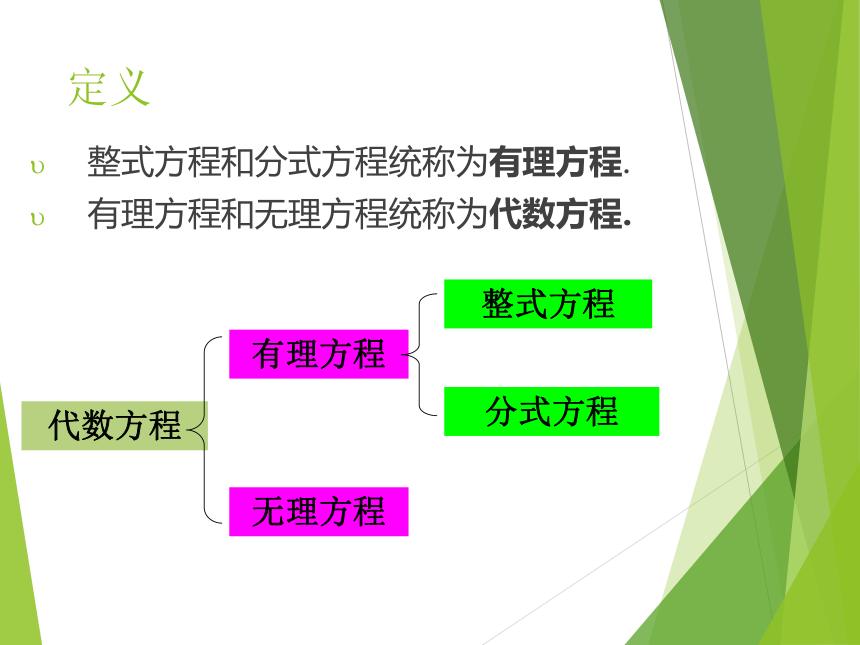
整式方程和分式方程统称为有理方程.
有理方程和无理方程统称为代数方程.
代数方程
有理方程
无理方程
整式方程
分式方程
巩固练习1
已知下列关于x的方程
其中无理方程是____________________(填序号).
(2)
(3)
(5)
怎样解方程
有理方程
无理方程
整式方程
分式方程
转化
转化
怎样将无理方程转化成有理方程?
去根号
方程变形的依据是什么?
无理方程
两边同时乘方
有理方程
将方程
两边同时平方
即
二次根式的性质:
解方程
方程两边平方,得
整理,得
解方程,得
它们都是原方程的根吗?
检验:把x=4代入原方程的两边,左边=4,右边=4
左边=右边, x=4是原方程的根
把x=-1代入原方程的两边,左边=-1,右边=1
左边≠右边, x=-1是原方程的增根,舍去
∴原方程的根是x=4
讨论:为什么会产生增根?
1、解无理方程的一般步骤是什么?
是
开始
去根号
解有理方程
检验
写出原方程的根
舍去
结束
无理方程如何进行“验根”?
代入原方程的左边和
右边,使左边=右边,
且根号有意义.
增根产生的原因是什么?
平方把无理方程化为
有理方程,使原方程
中未知数允许取值的
范围扩大了.
不是
例1 解下列方程:
(1)
.
课堂练习1
(1)
(2)
解下列方程:
(1)
(2)
2015上海中考
2017静安二模
X=2
X=1
思考
不解方程
你能判断这个方程实数根的情况吗?
是一个非负数
左边=一个非负数+1>0,右边=0,
所以原方程没有实数根.
归纳
课堂练习2
下列方程中,有实数根的方程是:( )
(A)
(B)
(C)
(D)
C
是一个非负数
……
请谈谈你的收获
课堂小结
解只含一个“根号”的无理方程时:
将“根号项”放在方程的一边
其它“项”放在方程的另一边
然后进行平方,化为有理方程.
作业布置
必做作业:练习册21.4
选做作业:
问题引入
观察
所列的方程有什么特点?它与前面所学的方程有什么区别?
已知一个实数x(x>0)的3倍与4的和的算术平方根等于它本身,求实数x.
21.4无理方程
定义
方程中含有根式,且被开方数是含有未知数的代数式,这样的方程叫做无理方程。无理方程也叫做根式方程。
辨一辨:下列方程是不是无理方程?若不是,则是什么方程?
(1)
(2)
(3)
整式方程
分式方程
无理方程
实数
有理数
无理数
整数
分数
有理式
无理式
代数式
整式
分式
代数方程
有理方程
无理方程
整式方程
分式方程
正整数
零
负整数
多项式
单项式
类比
定义
整式方程和分式方程统称为有理方程.
有理方程和无理方程统称为代数方程.
代数方程
有理方程
无理方程
整式方程
分式方程
巩固练习1
已知下列关于x的方程
其中无理方程是____________________(填序号).
(2)
(3)
(5)
怎样解方程
有理方程
无理方程
整式方程
分式方程
转化
转化
怎样将无理方程转化成有理方程?
去根号
方程变形的依据是什么?
无理方程
两边同时乘方
有理方程
将方程
两边同时平方
即
二次根式的性质:
解方程
方程两边平方,得
整理,得
解方程,得
它们都是原方程的根吗?
检验:把x=4代入原方程的两边,左边=4,右边=4
左边=右边, x=4是原方程的根
把x=-1代入原方程的两边,左边=-1,右边=1
左边≠右边, x=-1是原方程的增根,舍去
∴原方程的根是x=4
讨论:为什么会产生增根?
1、解无理方程的一般步骤是什么?
是
开始
去根号
解有理方程
检验
写出原方程的根
舍去
结束
无理方程如何进行“验根”?
代入原方程的左边和
右边,使左边=右边,
且根号有意义.
增根产生的原因是什么?
平方把无理方程化为
有理方程,使原方程
中未知数允许取值的
范围扩大了.
不是
例1 解下列方程:
(1)
.
课堂练习1
(1)
(2)
解下列方程:
(1)
(2)
2015上海中考
2017静安二模
X=2
X=1
思考
不解方程
你能判断这个方程实数根的情况吗?
是一个非负数
左边=一个非负数+1>0,右边=0,
所以原方程没有实数根.
归纳
课堂练习2
下列方程中,有实数根的方程是:( )
(A)
(B)
(C)
(D)
C
是一个非负数
……
请谈谈你的收获
课堂小结
解只含一个“根号”的无理方程时:
将“根号项”放在方程的一边
其它“项”放在方程的另一边
然后进行平方,化为有理方程.
作业布置
必做作业:练习册21.4
选做作业:
