沪教版(上海)数学八年级第二学期-21.6 二元二次方程组的解法(2) 课件(20张)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-21.6 二元二次方程组的解法(2) 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览



文档简介
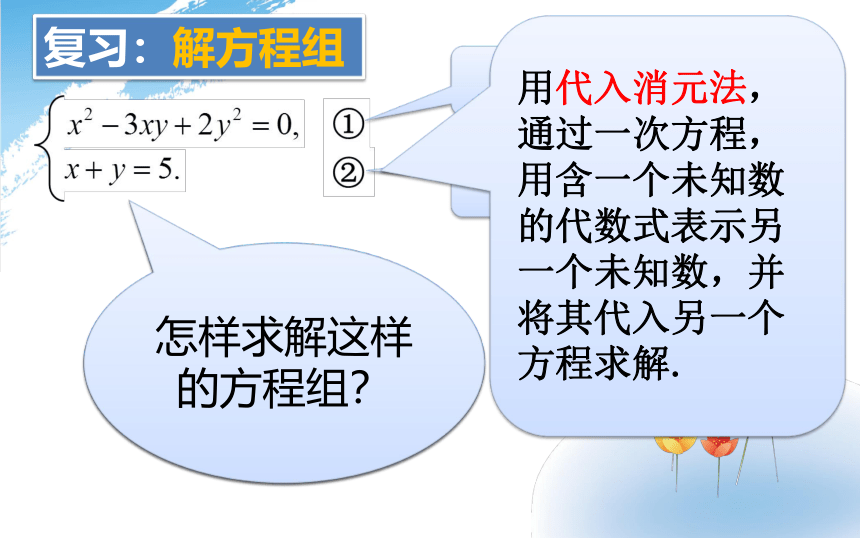
复习:解方程组
二元二次方程
二元一次方程
方程组中的
两个方程有
什么特点?
怎样求解这样的方程组?
用代入消元法,通过一次方程,用含一个未知数的代数式表示另一个未知数,并将其代入另一个方程求解.
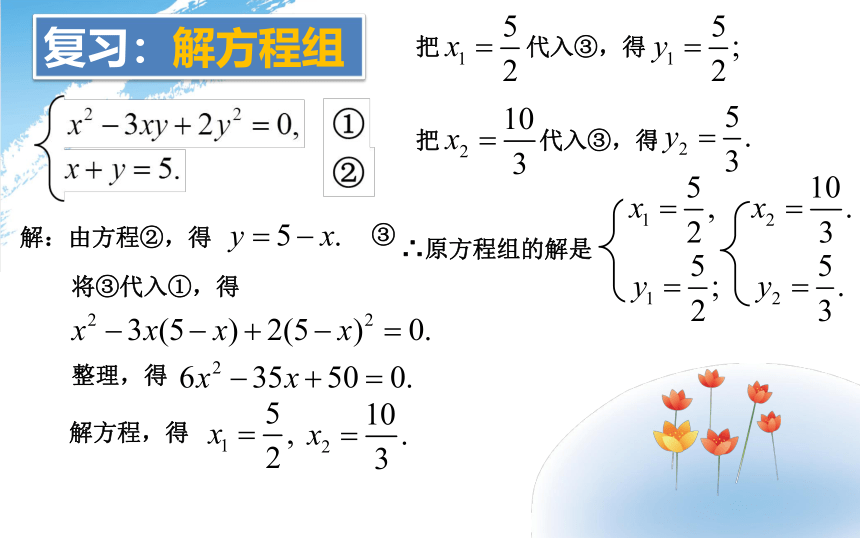
复习:解方程组
解:由方程②,得
③
将③代入①,得
整理,得
解方程,得
把 代入③,得
把 代入③,得
∴原方程组的解是
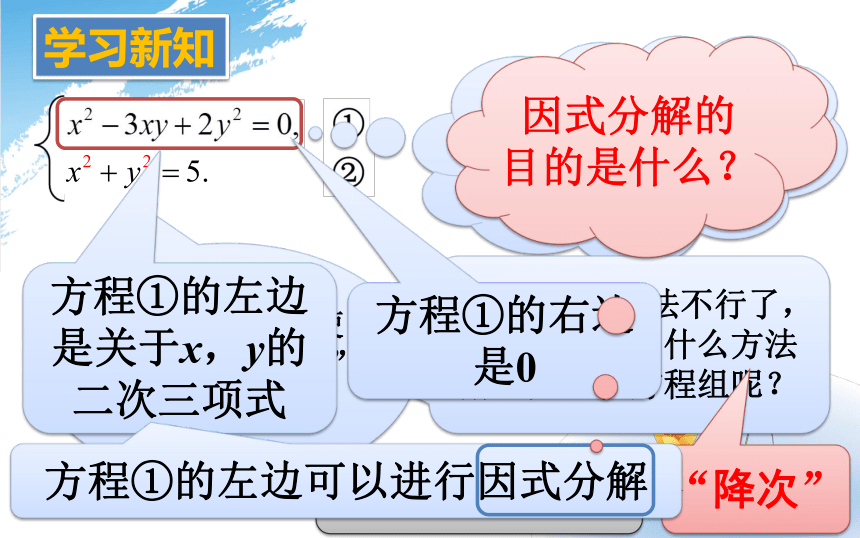
学习新知
现在还能直接使用“代入消元法”解答吗?
方程①
有什么特点?
方程①的左边是关于x,y的二次三项式
“消元”的方法不行了,那我们还能用什么方法解二元二次方程组呢?
“降次”
如何“降次”?
方程①的右边是0
方程①的左边可以进行因式分解
因式分解的目的是什么?
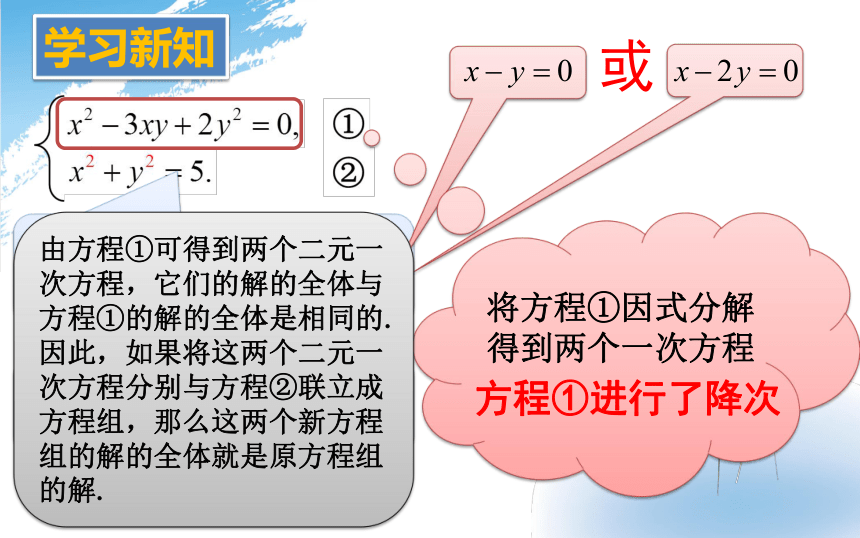
学习新知
方程①的左边分解因式,可变形为
由这个等式我们
可以得到什么?
或
将方程①因式分解得到两个一次方程
方程①进行了降次
由方程①可得到两个二元一次方程,它们的解的全体与方程①的解的全体是相同的.因此,如果将这两个二元一次方程分别与方程②联立成方程组,那么这两个新方程组的解的全体就是原方程组的解.
学习新知
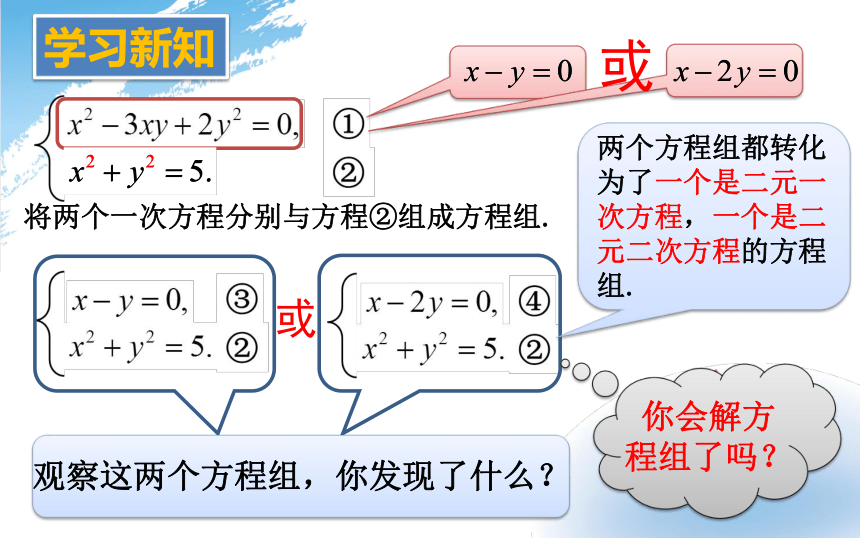
或
观察这两个方程组,你发现了什么?
两个方程组都转化为了一个是二元一次方程,一个是二元二次方程的方程组.
你会解方程组了吗?
将两个一次方程分别与方程②组成方程组.
或
学习新知
解:将方程①左边分解因式,
可变形为
得
或
.
将它们与方程②分别组成方程组,得:
或
(Ⅰ)
(Ⅱ)
解方程组(Ⅰ),得
解方程组(Ⅱ),得
∴原方程组的解是
像这样解特殊二元二次方程组的方法是因式分解法.
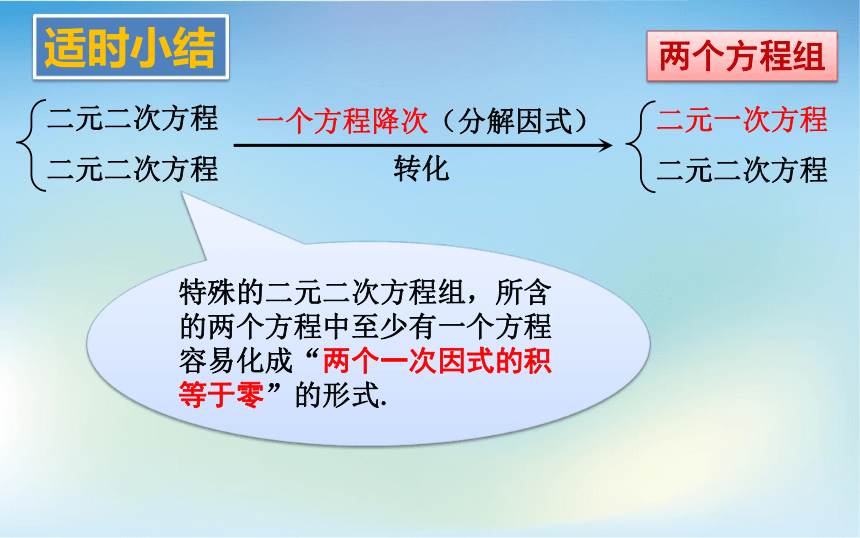
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
特殊的二元二次方程组,所含的两个方程中至少有一个方程容易化成“两个一次因式的积等于零”的形式.
反馈练习:解方程组
思考:方程组中哪个方程可以
因式分解?
如何分解因式?
反馈练习1:解方程组
解:将方程①左边分解因式,
可变形为
得
或
.
将它们与方程②分别组成方程组,得:
或
(Ⅰ)
(Ⅱ)
解方程组(Ⅰ),得
解方程组(Ⅱ),得
∴原方程组的解是
学习新知:例题3
方程①的左边可以分解因式.
思考:方程组中哪个方程可以
因式分解?
方程①可变形为:
方程②也可以分解因式.
方程②可变形为:
方程②两边开平方,得:
或
得
或
学习新知:例题3
得
或
得
或
原方程组化为4个二元一次方程组
学习新知:例题3
解:将方程①左边分解因式,
可变形为
得
或
.
方程②可变形为
两边开平方,得
或
原方程组化为4个二元一次方程组:
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
两个方程降次(分解因式)
转化
二元一次方程
二元一次方程
四个方程组
解二元二次方程组的基本思路是
“消元”
、
“降次”
.
反馈练习2:填空
解方程组
时,可以根据其特点把它化成
两个方程组,这两个方程组分别是:
,
.
反馈练习3:解方程组
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
原方程组化为4个二元一次方程组:
得
或
.
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
反馈练习4:解方程组
思考方程②的左边如何分解因式?
方程②的左边分解因式,可变形为:
化简得:
反馈练习4:解方程组
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
得
或
.
即
或
.
原方程组化为4个二元一次方程组:
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
课堂小结
两个方程分解因式(降次)
转化
二元一次方程
二元一次方程
四个方程组
二元二次方程
二元二次方程
一个方程分解因式(降次)
转化
二元一次方程
二元二次方程
两个方程组
布置作业:
练习册:习题21.6(2)
二元二次方程
二元一次方程
方程组中的
两个方程有
什么特点?
怎样求解这样的方程组?
用代入消元法,通过一次方程,用含一个未知数的代数式表示另一个未知数,并将其代入另一个方程求解.
复习:解方程组
解:由方程②,得
③
将③代入①,得
整理,得
解方程,得
把 代入③,得
把 代入③,得
∴原方程组的解是
学习新知
现在还能直接使用“代入消元法”解答吗?
方程①
有什么特点?
方程①的左边是关于x,y的二次三项式
“消元”的方法不行了,那我们还能用什么方法解二元二次方程组呢?
“降次”
如何“降次”?
方程①的右边是0
方程①的左边可以进行因式分解
因式分解的目的是什么?
学习新知
方程①的左边分解因式,可变形为
由这个等式我们
可以得到什么?
或
将方程①因式分解得到两个一次方程
方程①进行了降次
由方程①可得到两个二元一次方程,它们的解的全体与方程①的解的全体是相同的.因此,如果将这两个二元一次方程分别与方程②联立成方程组,那么这两个新方程组的解的全体就是原方程组的解.
学习新知
或
观察这两个方程组,你发现了什么?
两个方程组都转化为了一个是二元一次方程,一个是二元二次方程的方程组.
你会解方程组了吗?
将两个一次方程分别与方程②组成方程组.
或
学习新知
解:将方程①左边分解因式,
可变形为
得
或
.
将它们与方程②分别组成方程组,得:
或
(Ⅰ)
(Ⅱ)
解方程组(Ⅰ),得
解方程组(Ⅱ),得
∴原方程组的解是
像这样解特殊二元二次方程组的方法是因式分解法.
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
特殊的二元二次方程组,所含的两个方程中至少有一个方程容易化成“两个一次因式的积等于零”的形式.
反馈练习:解方程组
思考:方程组中哪个方程可以
因式分解?
如何分解因式?
反馈练习1:解方程组
解:将方程①左边分解因式,
可变形为
得
或
.
将它们与方程②分别组成方程组,得:
或
(Ⅰ)
(Ⅱ)
解方程组(Ⅰ),得
解方程组(Ⅱ),得
∴原方程组的解是
学习新知:例题3
方程①的左边可以分解因式.
思考:方程组中哪个方程可以
因式分解?
方程①可变形为:
方程②也可以分解因式.
方程②可变形为:
方程②两边开平方,得:
或
得
或
学习新知:例题3
得
或
得
或
原方程组化为4个二元一次方程组
学习新知:例题3
解:将方程①左边分解因式,
可变形为
得
或
.
方程②可变形为
两边开平方,得
或
原方程组化为4个二元一次方程组:
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
适时小结
二元二次方程
二元二次方程
一个方程降次(分解因式)
转化
二元一次方程
二元二次方程
两个方程组
两个方程降次(分解因式)
转化
二元一次方程
二元一次方程
四个方程组
解二元二次方程组的基本思路是
“消元”
、
“降次”
.
反馈练习2:填空
解方程组
时,可以根据其特点把它化成
两个方程组,这两个方程组分别是:
,
.
反馈练习3:解方程组
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
原方程组化为4个二元一次方程组:
得
或
.
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
反馈练习4:解方程组
思考方程②的左边如何分解因式?
方程②的左边分解因式,可变形为:
化简得:
反馈练习4:解方程组
解:将方程①变形为
两边开平方,得
或
方程②左边分解因式,可变形为
得
或
.
即
或
.
原方程组化为4个二元一次方程组:
分别解这4个方程组,得原方程组的解是
∴原方程组的解是
课堂小结
两个方程分解因式(降次)
转化
二元一次方程
二元一次方程
四个方程组
二元二次方程
二元二次方程
一个方程分解因式(降次)
转化
二元一次方程
二元二次方程
两个方程组
布置作业:
练习册:习题21.6(2)
