沪教版(上海)数学八年级第二学期-22.2 平行四边形的复习 课件(共22张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.2 平行四边形的复习 课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 822.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览







文档简介
平行四边形的复习
有两组对边分别平行的四边形叫做平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
平行四边形的定义
如图:四边形ABCD是平行四边形记作:
□ABCD
B
D
A
C
O
线段AC、BD就是□ABCD的两条对角线。
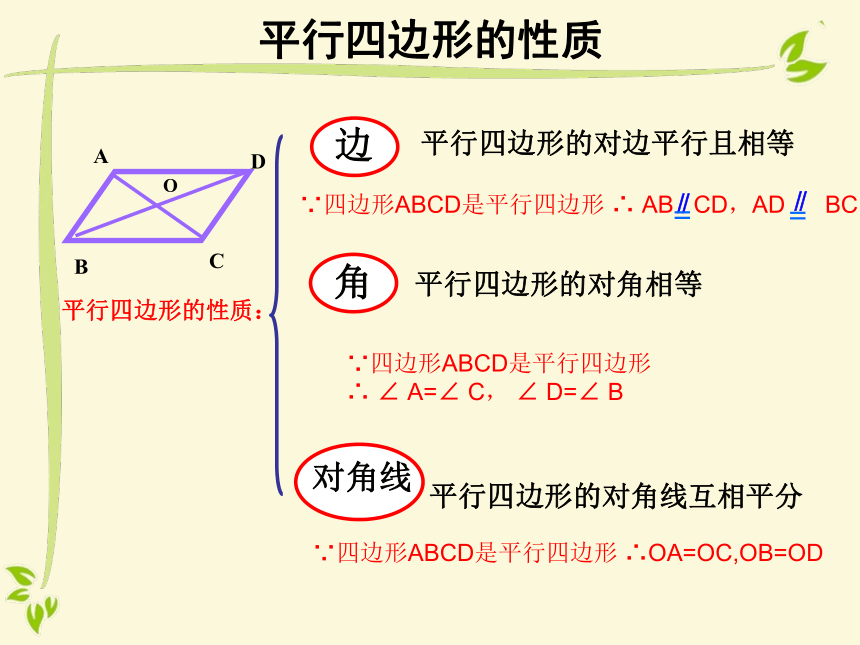
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴
AB
CD,AD
BC
∥
﹦
∥
﹦
平行四边形的对角相等
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
平行四边形的性质
∵四边形ABCD是平行四边形
∴
∠
A=∠
C,
∠
D=∠
B
●
A
D
O
C
B
D
B
O
C
A
看一看
说明了什么?
□ABCD是
中心对称图形,对称中心是两条对角线的交点。
基础练行四边形的对边__且__;对角__。
平行四边形相邻两角之比是2:3
,
各角分别是多少度?
3.
□ABCD中,AB=5,BC=3,求它的周长。
E
A
B
D
C
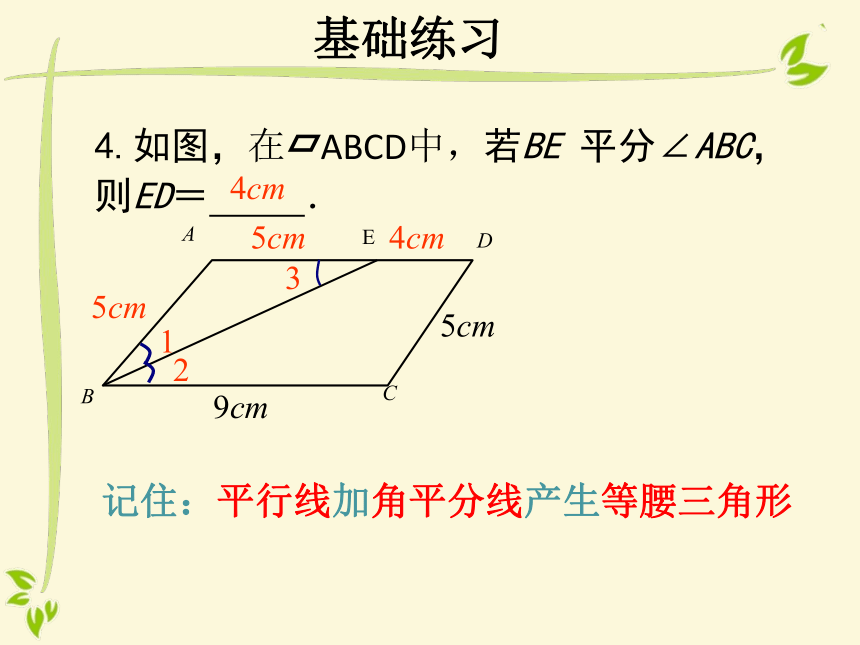
9cm
5cm
4.如图,在
ABCD中,若BE
平分∠ABC,则ED=
.
4cm
2
3
5cm
5cm
4cm
1
基础练习
记住:平行线加角平分线产生等腰三角形
O
D
B
A
C
1.如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC+BD=20,
△AOB的周长等于15,
则CD=______.
5
小组讨论,请代表回答
2.如图,在
ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是
_________.
O
D
B
A
C
●
1<AD<9
3.如图,在平面直角坐标系中,
OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为(
)
x
Y
C
O
(0,0)
B(5,0)
D(2,3)
A.
(3,7)
B.
(5,3)
C.
(7,3)
D.
(8,2)
C
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
理一理
1.请你识别下列四边形哪些是平行四边形?为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
大显身手
D
A
B
C
E
F
证法1:
∵四边形ABCD是平行四边形
AD
∥
BC且AD
=BC
EAD=
FCB
AE=CF
EAD=
FCB
AD=BC
AED
≌
CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在
AED和
CFB中
同理可证:BE=DF
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证法2:联结BD,交AC于点O。
∵四边形ABCD是平行四边形
∴
AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又
BO=DO
∴
四边形BFDE是平行四边形
小组讨论
如图,D,E在三角形ABC的边BC上,F、G分别在AC、
AB边上,DF
与EG互相平分,且DF∥AB,EG∥AC.
求证:BD=DE=EC.
G
D
C
B
A
F
E
找一找
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
在这些图形中面积被平分的图形有哪些?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分
小明家有一块平行四边形菜地,菜地中间有一口井,为了浇水的方便,小明建议妈妈经过水井修一条路,可以把菜地分成面积相等的两部分.
同学们,你知道聪明的小明是怎么帮妈妈分的吗?
B
M
C
●
D
A
O
思考
如何用一条直线把下面这个图形的面积一分为二?
思考
“司马光砸缸”的故事传送千古,要从水缸中救人,就要使人离开水。如果一时无法让人离开缸和水,也可以让水离开缸和人,同样可以实现救人的目的。司马光的机智在于在短时间内通过问题转换实现了救人目的。
问题转换
1、对自己说,你有什么收获?
2、对同学说,你有什么温馨提示?
3、对老师说,你有什么疑惑?
小结
(1)平行四边形的对边相等;
(2)平行四边形的对边平行;
(3)平行四边形的对角相等;
(4)平行四边形的对角线互相平分.
(4)
对角线互相平分的四边形是平行四边形.
(1)
两组对边分别平行的四边形是平行四边形.
(2)
一组对边平行且相等的四边形是平行四边形.
(3)
两组对边分别相等的四边形是平行四边形.
平行四边形的性质:
平行四边形的判定方法:
谢谢!
有两组对边分别平行的四边形叫做平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
平行四边形的定义
如图:四边形ABCD是平行四边形记作:
□ABCD
B
D
A
C
O
线段AC、BD就是□ABCD的两条对角线。
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴
AB
CD,AD
BC
∥
﹦
∥
﹦
平行四边形的对角相等
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
平行四边形的性质
∵四边形ABCD是平行四边形
∴
∠
A=∠
C,
∠
D=∠
B
●
A
D
O
C
B
D
B
O
C
A
看一看
说明了什么?
□ABCD是
中心对称图形,对称中心是两条对角线的交点。
基础练行四边形的对边__且__;对角__。
平行四边形相邻两角之比是2:3
,
各角分别是多少度?
3.
□ABCD中,AB=5,BC=3,求它的周长。
E
A
B
D
C
9cm
5cm
4.如图,在
ABCD中,若BE
平分∠ABC,则ED=
.
4cm
2
3
5cm
5cm
4cm
1
基础练习
记住:平行线加角平分线产生等腰三角形
O
D
B
A
C
1.如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC+BD=20,
△AOB的周长等于15,
则CD=______.
5
小组讨论,请代表回答
2.如图,在
ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是
_________.
O
D
B
A
C
●
1<AD<9
3.如图,在平面直角坐标系中,
OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为(
)
x
Y
C
O
(0,0)
B(5,0)
D(2,3)
A.
(3,7)
B.
(5,3)
C.
(7,3)
D.
(8,2)
C
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
理一理
1.请你识别下列四边形哪些是平行四边形?为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
大显身手
D
A
B
C
E
F
证法1:
∵四边形ABCD是平行四边形
AD
∥
BC且AD
=BC
EAD=
FCB
AE=CF
EAD=
FCB
AD=BC
AED
≌
CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在
AED和
CFB中
同理可证:BE=DF
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证法2:联结BD,交AC于点O。
∵四边形ABCD是平行四边形
∴
AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又
BO=DO
∴
四边形BFDE是平行四边形
小组讨论
如图,D,E在三角形ABC的边BC上,F、G分别在AC、
AB边上,DF
与EG互相平分,且DF∥AB,EG∥AC.
求证:BD=DE=EC.
G
D
C
B
A
F
E
找一找
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
在这些图形中面积被平分的图形有哪些?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分
小明家有一块平行四边形菜地,菜地中间有一口井,为了浇水的方便,小明建议妈妈经过水井修一条路,可以把菜地分成面积相等的两部分.
同学们,你知道聪明的小明是怎么帮妈妈分的吗?
B
M
C
●
D
A
O
思考
如何用一条直线把下面这个图形的面积一分为二?
思考
“司马光砸缸”的故事传送千古,要从水缸中救人,就要使人离开水。如果一时无法让人离开缸和水,也可以让水离开缸和人,同样可以实现救人的目的。司马光的机智在于在短时间内通过问题转换实现了救人目的。
问题转换
1、对自己说,你有什么收获?
2、对同学说,你有什么温馨提示?
3、对老师说,你有什么疑惑?
小结
(1)平行四边形的对边相等;
(2)平行四边形的对边平行;
(3)平行四边形的对角相等;
(4)平行四边形的对角线互相平分.
(4)
对角线互相平分的四边形是平行四边形.
(1)
两组对边分别平行的四边形是平行四边形.
(2)
一组对边平行且相等的四边形是平行四边形.
(3)
两组对边分别相等的四边形是平行四边形.
平行四边形的性质:
平行四边形的判定方法:
谢谢!
