沪教版(上海)数学七年级第二学期-13章小结 平行线的性质(复习课) 课件(共21张ppt)
文档属性
| 名称 | 沪教版(上海)数学七年级第二学期-13章小结 平行线的性质(复习课) 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 405.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览


文档简介
平行线复习
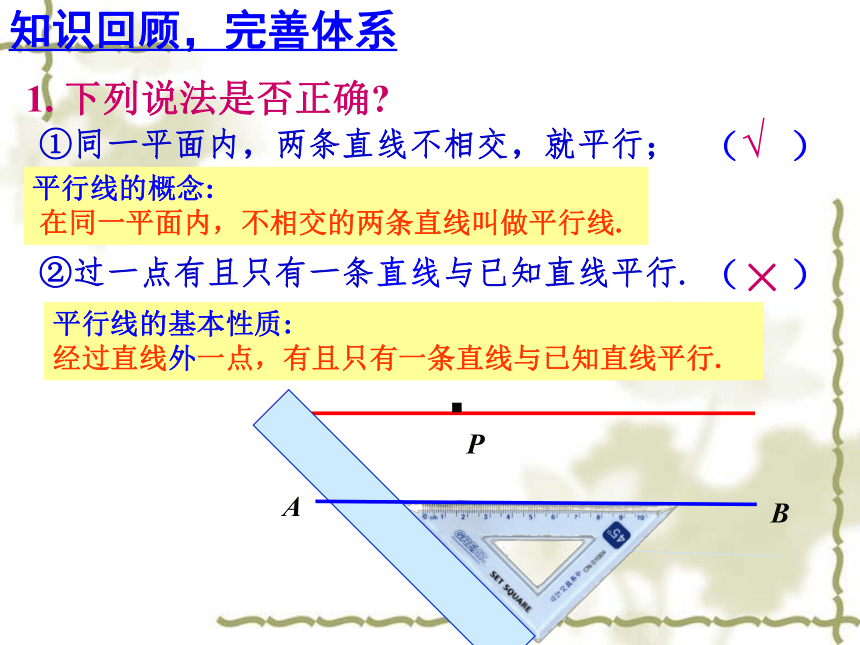
①同一平面内,两条直线不相交,就平行;
平行线的概念:
在同一平面内,不相交的两条直线叫做平行线.
平行线的基本性质:
经过直线外一点,有且只有一条直线与已知直线平行.
知识回顾,完善体系
②过一点有且只有一条直线与已知直线平行.
·
A
B
P
1. 下列说法是否正确?
√
×
( )
( )
③如果a∥b,b∥c,那么a∥c.
④同一平面内,如果a⊥b,b⊥c,那么a∥c.
平行的传递性:
平行于同一条直线的两条直线互相平行.
同一平面内,垂直于同一条直线的两直线互相平行.
a
b
c
a
b
c
知识回顾,完善体系
√
√
( )
( )
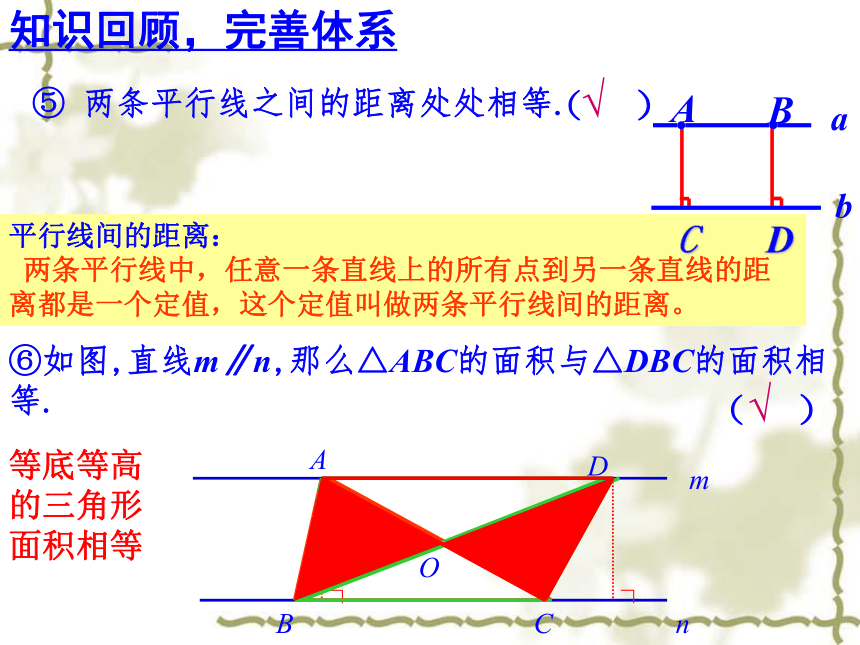
平行线间的距离:
两条平行线中,任意一条直线上的所有点到另一条直线的距离都是一个定值,这个定值叫做两条平行线间的距离。
⑤ 两条平行线之间的距离处处相等.
A
B
C
D
O
m
n
∟
∟
⑥如图,直线m∥n,那么△ABC的面积与△DBC的面积相等.
知识回顾,完善体系
√
√
C
D
A
B
等底等高
的三角形
面积相等
( )
( )
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
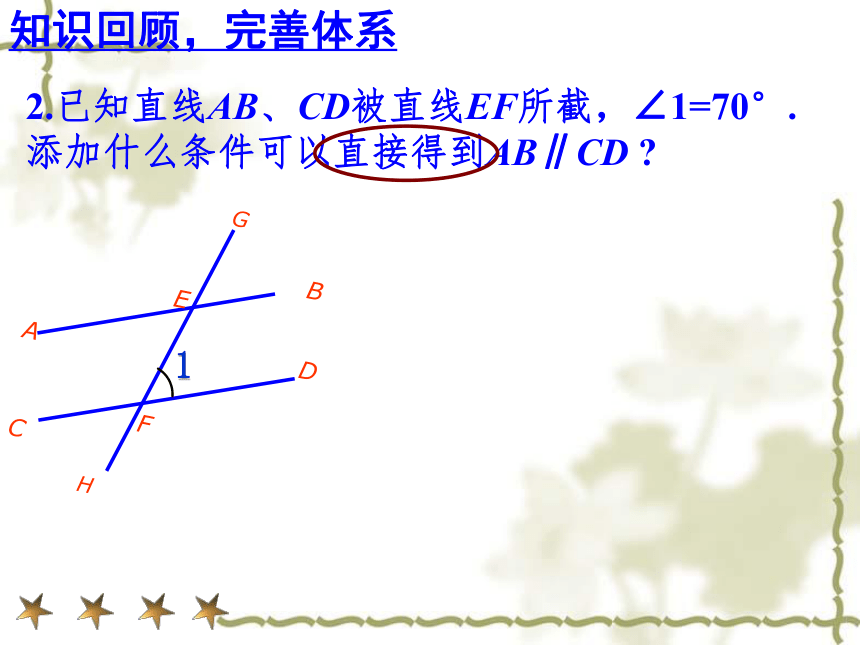
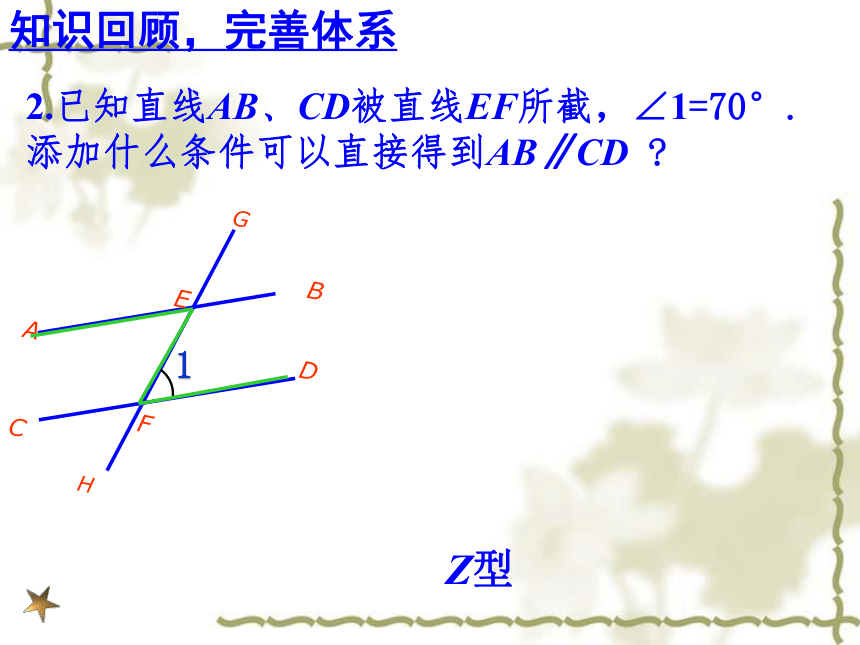
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
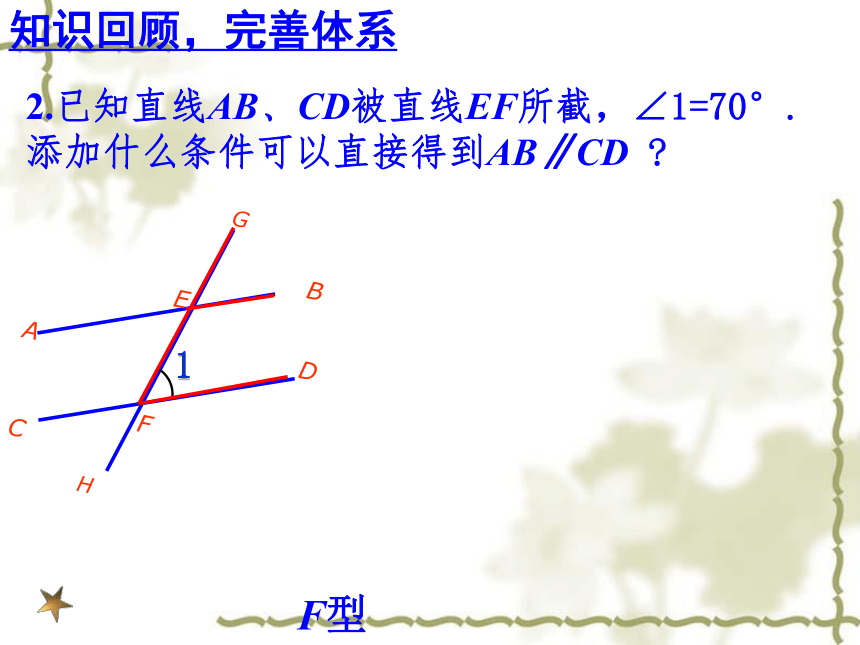
F型
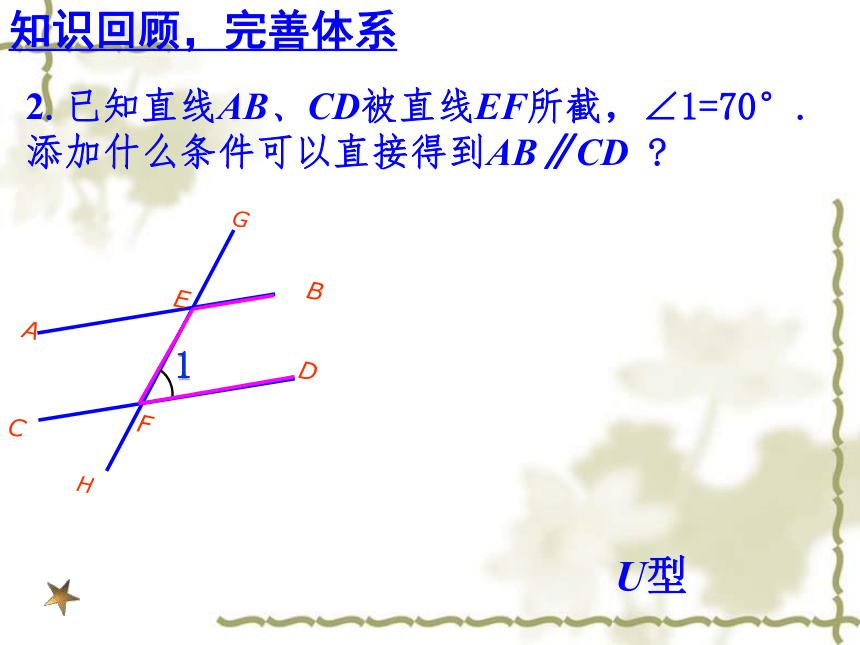
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
Z型
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
U型
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
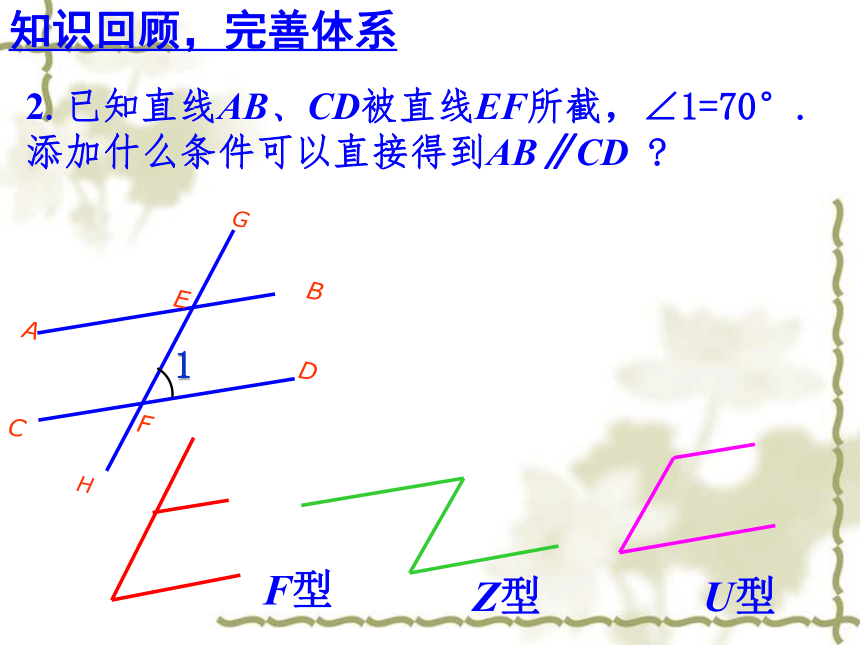
F型
Z型
U型
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
直线平行
角的关系
平行线的判定定理
知识回顾,完善体系
3.如图所示,已知a∥b, c∥d, ∠4=110°,
求∠1 、∠2、∠3的度数.
知识回顾,完善体系
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
平行线的性质
角的关系
直线平行
知识回顾,完善体系
平行
角的关系
性质
判定
两条不同直线
同一平面内的
相交直线
平行直线
平行线的基本性质
平行线间的距离
判定方法与性质
知识回顾,完善体系
……
(2)∵CG // DF(已知)
∴∠2= ( )
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
G
5
4
3
F
E
D
C
B
A
2
1
A
B
E
D
1
G
C
F
D
2
运用知识,培养能力
(1)∵∠B=∠1(已知)
∴____//____( )
平行线的判定
平行线的性质
例1 看图填空
例1 看图填空
(4)∵∠3=∠A(已知)
∴____//____( )
(3)∵AG // DF(已知)
∴∠3=_____( )
B
A
G
D
3
A
G
D
3
F
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
G
5
4
3
F
E
D
C
B
A
2
1
运用知识,培养能力
(5)∵∠B+∠4=180°(已知)
∴____//____( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
A
B
D
E
4
G
C
F
D
5
AB
DE
同旁内角互补,两直线平行
∠5
两直线平行,同旁内角互补
G
5
4
3
F
E
D
C
B
A
2
1
例1 看图填空
运用知识,培养能力
F
D
B
E
A
C
G
H
N
M
1
2
例3:如图,AB∥CD,直线FE与两平行线交于点G、H, GM和NH分别平分∠BGH和∠CHG. ∠1和∠2是否相等?为什么?
运用知识,培养能力
A
C
P
B
D
变式1: AB∥CD,将点P移至如图所示, ∠PCD=α,∠PAB=β, ∠APC=γ此时α、β、γ满足的数量关系为____________.
α
β
γ
1
2
α+β+γ=360°
拓展提高
E
A
C
P
B
D
变式2: AB∥CD, 将点P移至如图所示, ∠PCD=α,
∠ PAB=β, ∠APC=γ此时α、β、γ满足怎样的数量关系?
α
β
E
拓展提高
γ
A
C
P
B
D
变式3: AB∥CD,将点P移至如图所示, ∠PCD=α,
∠ PAB=β, ∠APC=γ此时α、β、γ满足怎样的数量关系?
α
β
E
拓展提高
γ
收获与体会
①同一平面内,两条直线不相交,就平行;
平行线的概念:
在同一平面内,不相交的两条直线叫做平行线.
平行线的基本性质:
经过直线外一点,有且只有一条直线与已知直线平行.
知识回顾,完善体系
②过一点有且只有一条直线与已知直线平行.
·
A
B
P
1. 下列说法是否正确?
√
×
( )
( )
③如果a∥b,b∥c,那么a∥c.
④同一平面内,如果a⊥b,b⊥c,那么a∥c.
平行的传递性:
平行于同一条直线的两条直线互相平行.
同一平面内,垂直于同一条直线的两直线互相平行.
a
b
c
a
b
c
知识回顾,完善体系
√
√
( )
( )
平行线间的距离:
两条平行线中,任意一条直线上的所有点到另一条直线的距离都是一个定值,这个定值叫做两条平行线间的距离。
⑤ 两条平行线之间的距离处处相等.
A
B
C
D
O
m
n
∟
∟
⑥如图,直线m∥n,那么△ABC的面积与△DBC的面积相等.
知识回顾,完善体系
√
√
C
D
A
B
等底等高
的三角形
面积相等
( )
( )
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
F型
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
Z型
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
U型
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
A
B
C
D
E
F
G
H
1
知识回顾,完善体系
F型
Z型
U型
2.已知直线AB、CD被直线EF所截,∠1=70°. 添加什么条件可以直接得到AB∥CD ?
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
直线平行
角的关系
平行线的判定定理
知识回顾,完善体系
3.如图所示,已知a∥b, c∥d, ∠4=110°,
求∠1 、∠2、∠3的度数.
知识回顾,完善体系
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
平行线的性质
角的关系
直线平行
知识回顾,完善体系
平行
角的关系
性质
判定
两条不同直线
同一平面内的
相交直线
平行直线
平行线的基本性质
平行线间的距离
判定方法与性质
知识回顾,完善体系
……
(2)∵CG // DF(已知)
∴∠2= ( )
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
G
5
4
3
F
E
D
C
B
A
2
1
A
B
E
D
1
G
C
F
D
2
运用知识,培养能力
(1)∵∠B=∠1(已知)
∴____//____( )
平行线的判定
平行线的性质
例1 看图填空
例1 看图填空
(4)∵∠3=∠A(已知)
∴____//____( )
(3)∵AG // DF(已知)
∴∠3=_____( )
B
A
G
D
3
A
G
D
3
F
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
G
5
4
3
F
E
D
C
B
A
2
1
运用知识,培养能力
(5)∵∠B+∠4=180°(已知)
∴____//____( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
A
B
D
E
4
G
C
F
D
5
AB
DE
同旁内角互补,两直线平行
∠5
两直线平行,同旁内角互补
G
5
4
3
F
E
D
C
B
A
2
1
例1 看图填空
运用知识,培养能力
F
D
B
E
A
C
G
H
N
M
1
2
例3:如图,AB∥CD,直线FE与两平行线交于点G、H, GM和NH分别平分∠BGH和∠CHG. ∠1和∠2是否相等?为什么?
运用知识,培养能力
A
C
P
B
D
变式1: AB∥CD,将点P移至如图所示, ∠PCD=α,∠PAB=β, ∠APC=γ此时α、β、γ满足的数量关系为____________.
α
β
γ
1
2
α+β+γ=360°
拓展提高
E
A
C
P
B
D
变式2: AB∥CD, 将点P移至如图所示, ∠PCD=α,
∠ PAB=β, ∠APC=γ此时α、β、γ满足怎样的数量关系?
α
β
E
拓展提高
γ
A
C
P
B
D
变式3: AB∥CD,将点P移至如图所示, ∠PCD=α,
∠ PAB=β, ∠APC=γ此时α、β、γ满足怎样的数量关系?
α
β
E
拓展提高
γ
收获与体会
