沪科版七年级数学下册课件-8.3 完全平方公式与平方差公式3(共15张ppt)
文档属性
| 名称 | 沪科版七年级数学下册课件-8.3 完全平方公式与平方差公式3(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 395.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 12:19:57 | ||
图片预览




文档简介
8.3 完全平方公式与平方差公式
故事导入
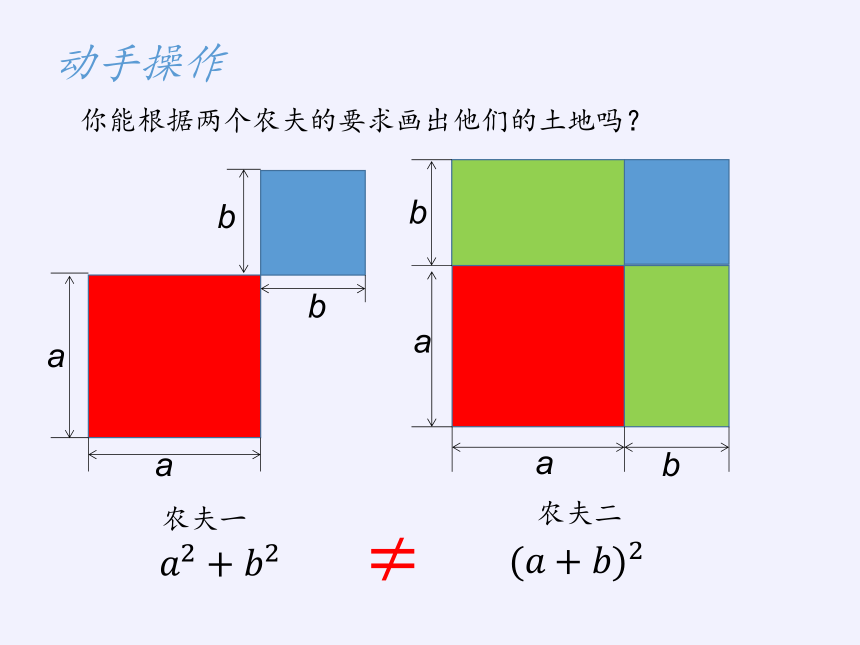
很久很久以前,有一个国家的土地都要求是正方形的。有一天,这个国家的公主被妖怪抓到了森林里,两个农夫在森林里打猎时打死了妖怪救出了公主。国王为了感谢要赏赐他们,这两个农夫原本各有一块边长为a米的正方形土地,第一个农夫对国王说:“您可不可以再给我一块边长为b米的土地呢?”国王答应了他,问第二个农夫:“你是不是要跟他一样呢?”第二个农夫说:“不,我只要您将我原来的土地边长增加b米就好了。”
国王想不通了,他说:“你们的要求不是一样的吗?”
动手操作
你能根据两个农夫的要求画出他们的土地吗?
a
a
b
b
a
b
a
b
农夫一
农夫二
????2+????2
?
(????+????)2
?
≠
?
新知探究
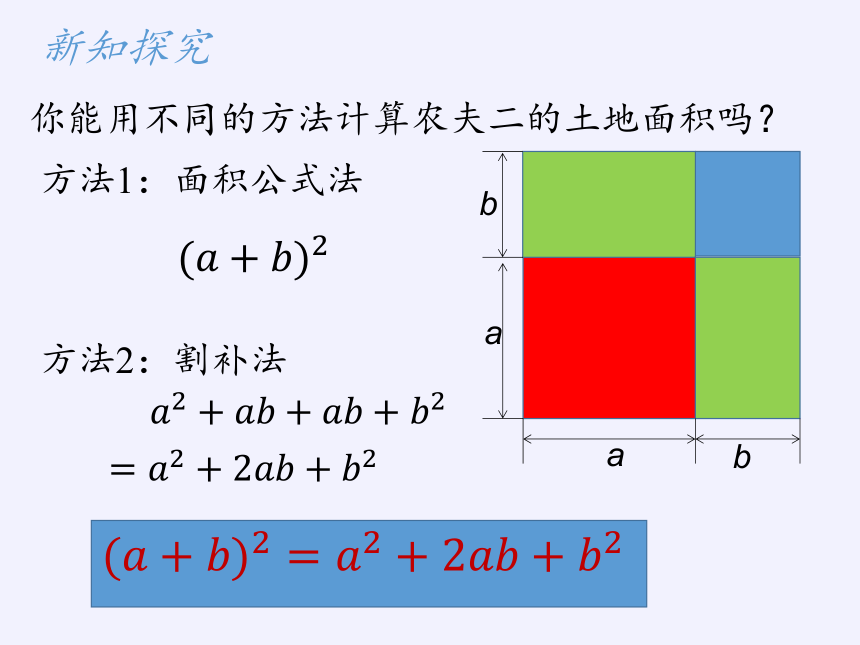
你能用不同的方法计算农夫二的土地面积吗?
a
b
a
b
方法1:面积公式法
(????+????)2
?
方法2:割补法
????2+????????+????????+????2
?
=????2+2????????+????2
?
(????+????)2=????2+2????????+????2
?
(????+????)2=????2+2????????+????2
?
还有别的方法验证吗?
(????+????)2=(????+????)(????+????)
?
=????2+????????+????????+????2
?
=????2+2????????+????2
?
你能用语言描述上述公式吗?
两个数和的平方,等于这两个数的平方和加上这两个数乘积的2倍。
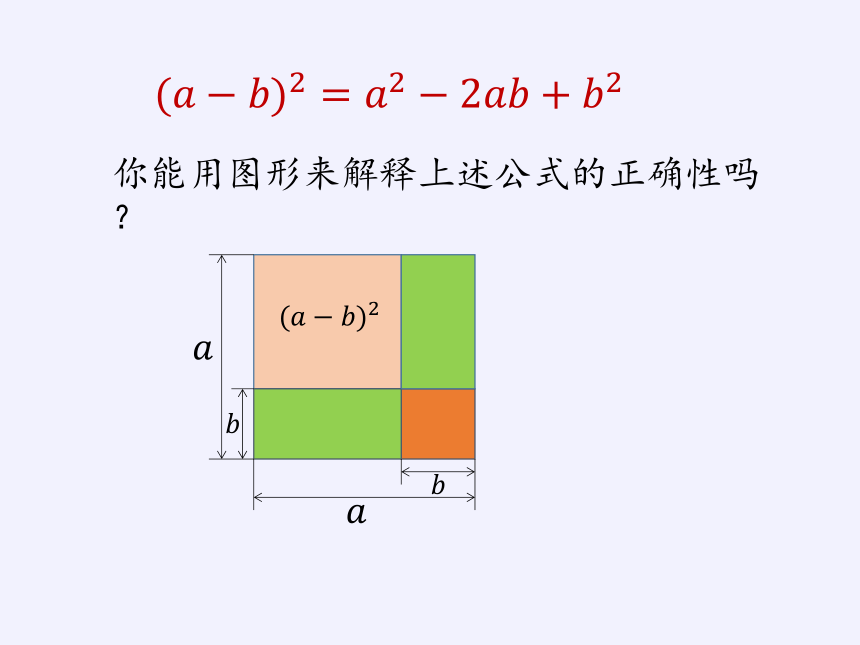
(?????????)2=????2?2????????+????2
?
思考:(?????????)2结果又是多少呢?你是怎么验证的?
?
语言描述:两个数差的平方,等于这两个数的平方和减去这两个数乘积的2倍。
(?????????)2=????2?2????????+????2
?
你能用图形来解释上述公式的正确性吗?
????
?
????
?
????
?
????
?
(?????????)2
?
完全平方公式
(????+????)2=????2+2????????+????2
?
(?????????)2=????2?2????????+????2
?
归纳总结
结构特征:
(1)左边是和(或差)的平方;
(2)右边是二次三项式,其中两项是 平方,另一项是乘积的2倍。
注意:公式中????, ????可以表示数,也可以是单项式或多项式。
?
口诀:首平方,尾平方,乘积2倍放中央,符号看前方。
例 1 利用完全平方公式计算:
(1)
(2????+????)2;
?
(2)
(3?????2????)2;
?
重要提示:
运用公式计算,要先识别公式中的????, ????
在具体式子中分别表示什么。
?
解
(1)
(2????+????)2
?
=
?
(????+????)2=????2+2????????+????2
?
(2????)2+2?2?????????+????2
?
4????2+4????????+????2
?
=
?
(?????????)2=????2?2????????+????2
?
(2)
(3?????2????)2
?
=
?
(3????)2?2?3?????2????+(2????)2
?
=
?
9????2?12????????+4????2
?
例 2 计算:
(1)
(?3????+2)2;
?
(2)
(?2?????????)2.
?
解
(1)
(?3????+2)2
?
(????+????)2=????2+2????????+????2
?
=
?
(?3????)2+2?(?3????)?2+22
?
=
?
9????2?12????+4
?
(2)
(?2?????????)2
?
=
?
(?2????)2?2?(?2????)?????+????2
?
=
?
4????2+4????????+????2
?
(?????????)2=????2?2????????+????2
?
思考:本题还有其他解法吗?
练 习:教材69页
1.利用乘法公式计算:
(2)
(?????3????)2;
?
(3)
(2????+????2)2;
?
(4)
(?2????+3????)2
?
(3????+1)2;
?
(1)
2.如图,是一张正方形的纸片,如果把它沿着各边都剪去3????????宽的一条,那么所得小正方形的面积比原正方形的面积减少了84????????2,求原正方形的边长。
?
3
(单位:????????)
?
3
课堂小结
通过本节课的学习,你有哪些收获?
1.完全平方公式:
2.数学方法和思想:
(????+????)2=????2+2????????+????2
?
(?????????)2=????2?2????????+????2
?
数形结合以及方程思想
谢 谢
故事导入
很久很久以前,有一个国家的土地都要求是正方形的。有一天,这个国家的公主被妖怪抓到了森林里,两个农夫在森林里打猎时打死了妖怪救出了公主。国王为了感谢要赏赐他们,这两个农夫原本各有一块边长为a米的正方形土地,第一个农夫对国王说:“您可不可以再给我一块边长为b米的土地呢?”国王答应了他,问第二个农夫:“你是不是要跟他一样呢?”第二个农夫说:“不,我只要您将我原来的土地边长增加b米就好了。”
国王想不通了,他说:“你们的要求不是一样的吗?”
动手操作
你能根据两个农夫的要求画出他们的土地吗?
a
a
b
b
a
b
a
b
农夫一
农夫二
????2+????2
?
(????+????)2
?
≠
?
新知探究
你能用不同的方法计算农夫二的土地面积吗?
a
b
a
b
方法1:面积公式法
(????+????)2
?
方法2:割补法
????2+????????+????????+????2
?
=????2+2????????+????2
?
(????+????)2=????2+2????????+????2
?
(????+????)2=????2+2????????+????2
?
还有别的方法验证吗?
(????+????)2=(????+????)(????+????)
?
=????2+????????+????????+????2
?
=????2+2????????+????2
?
你能用语言描述上述公式吗?
两个数和的平方,等于这两个数的平方和加上这两个数乘积的2倍。
(?????????)2=????2?2????????+????2
?
思考:(?????????)2结果又是多少呢?你是怎么验证的?
?
语言描述:两个数差的平方,等于这两个数的平方和减去这两个数乘积的2倍。
(?????????)2=????2?2????????+????2
?
你能用图形来解释上述公式的正确性吗?
????
?
????
?
????
?
????
?
(?????????)2
?
完全平方公式
(????+????)2=????2+2????????+????2
?
(?????????)2=????2?2????????+????2
?
归纳总结
结构特征:
(1)左边是和(或差)的平方;
(2)右边是二次三项式,其中两项是 平方,另一项是乘积的2倍。
注意:公式中????, ????可以表示数,也可以是单项式或多项式。
?
口诀:首平方,尾平方,乘积2倍放中央,符号看前方。
例 1 利用完全平方公式计算:
(1)
(2????+????)2;
?
(2)
(3?????2????)2;
?
重要提示:
运用公式计算,要先识别公式中的????, ????
在具体式子中分别表示什么。
?
解
(1)
(2????+????)2
?
=
?
(????+????)2=????2+2????????+????2
?
(2????)2+2?2?????????+????2
?
4????2+4????????+????2
?
=
?
(?????????)2=????2?2????????+????2
?
(2)
(3?????2????)2
?
=
?
(3????)2?2?3?????2????+(2????)2
?
=
?
9????2?12????????+4????2
?
例 2 计算:
(1)
(?3????+2)2;
?
(2)
(?2?????????)2.
?
解
(1)
(?3????+2)2
?
(????+????)2=????2+2????????+????2
?
=
?
(?3????)2+2?(?3????)?2+22
?
=
?
9????2?12????+4
?
(2)
(?2?????????)2
?
=
?
(?2????)2?2?(?2????)?????+????2
?
=
?
4????2+4????????+????2
?
(?????????)2=????2?2????????+????2
?
思考:本题还有其他解法吗?
练 习:教材69页
1.利用乘法公式计算:
(2)
(?????3????)2;
?
(3)
(2????+????2)2;
?
(4)
(?2????+3????)2
?
(3????+1)2;
?
(1)
2.如图,是一张正方形的纸片,如果把它沿着各边都剪去3????????宽的一条,那么所得小正方形的面积比原正方形的面积减少了84????????2,求原正方形的边长。
?
3
(单位:????????)
?
3
课堂小结
通过本节课的学习,你有哪些收获?
1.完全平方公式:
2.数学方法和思想:
(????+????)2=????2+2????????+????2
?
(?????????)2=????2?2????????+????2
?
数形结合以及方程思想
谢 谢
