沪科版数学九年级上册21.3《二次函数与一元二次方程》课件(3) (共16张ppt)
文档属性
| 名称 | 沪科版数学九年级上册21.3《二次函数与一元二次方程》课件(3) (共16张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览


文档简介
二次函数中的符号问题
(a、b、c、△等符号)
X
归纳知识点:
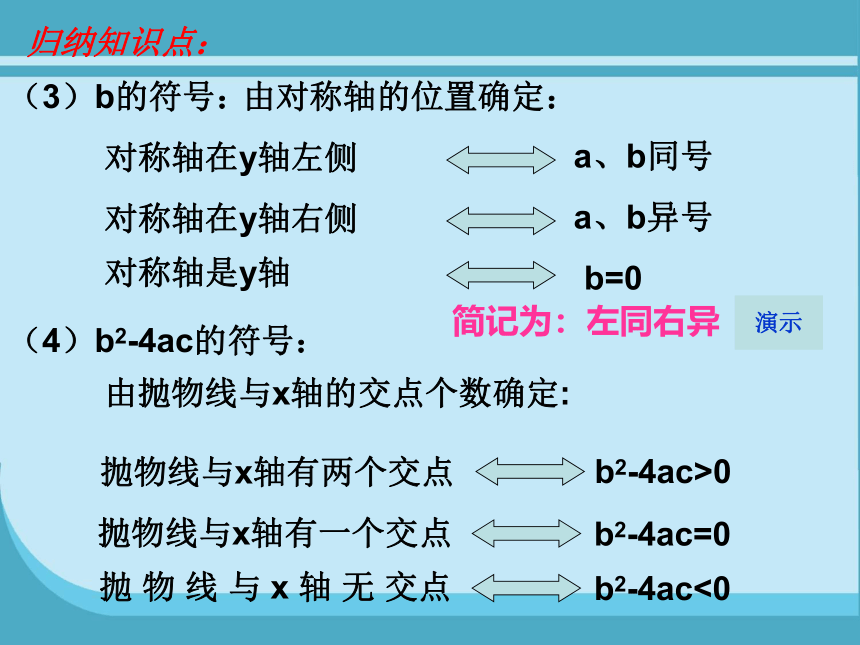
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定:
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
(3)b的符号:
由对称轴的位置确定:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定:
抛物线与x轴有两个交点
b2-4ac>0
抛物线与x轴有一个交点
b2-4ac=0
抛 物 线 与 x 轴 无 交点
b2-4ac<0
归纳知识点:
简记为:左同右异
演示
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(5)a+b+c的符号:
由x=1时抛物线上的点的位置确定
(6)a-b+c的符号:
由x=-1时抛物线上的点的位置确定
利用以上知识主要解决以下几方面问题:
(1)由a,b,c,?的符号确定抛物线在坐标系中的大 致位置;
(2)由抛物线的位置确定系数a,b,c,?等符号及有
关a,b,c的代数式的符号;
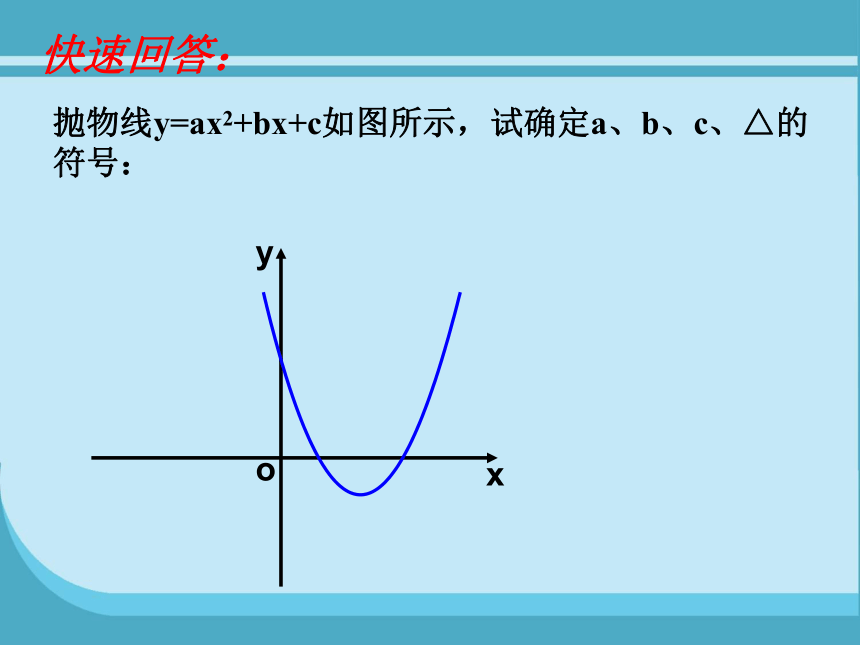
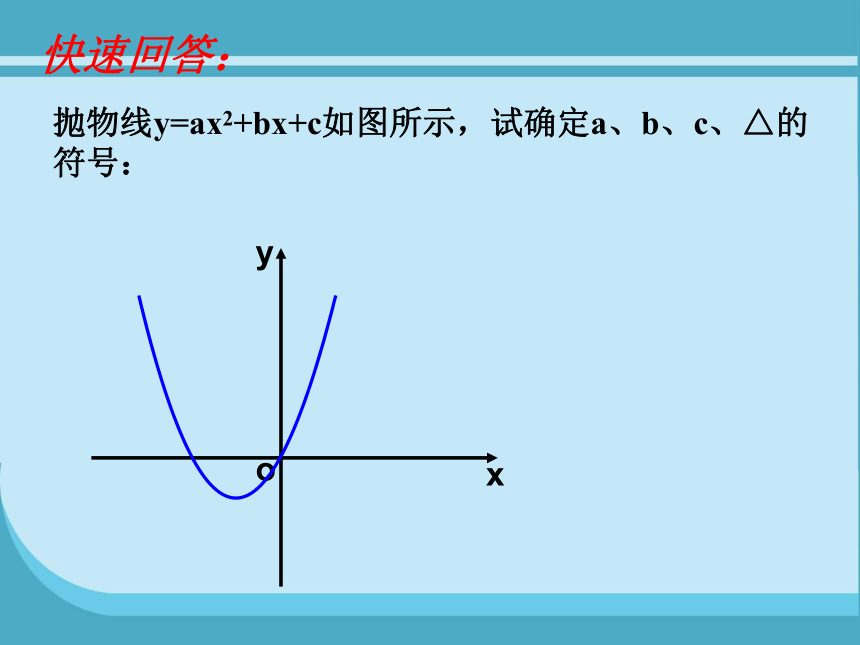
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
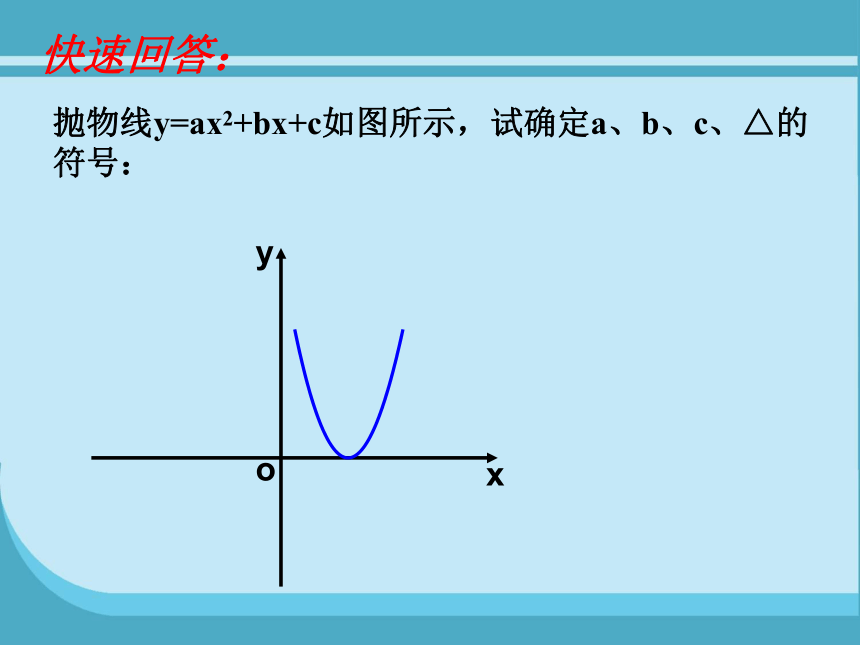
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
练一练:
1.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )
A、第一象限
B、第二象限
C、第三象限
D、第四象限
x
o
y
D
练一练:
2、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个
x
o
y
x=1
B
练一练:
3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
4.如图,直线x= –1是二次函数
的图象的对称轴,则下列代数式abc,a+b+c,b2-4ac,2a-b,3a-b中负数有( )个
(A)1(B)2(C)3(D)4
练一练:
-2
二次函数y=ax2+bx+c(a≠0)的几个特例:
1、当x=1 时,
2、当x=-1时,
3、当x=2时,
4、当x=-2时,
y=a+b+c
y=a-b+c
y=4a+2b+c
y=4a-2b+c
…………… ……………
x
y
o
1
-1
2
练习:二次函数y=ax2+bx+c(a≠0)的图象如上图所示,那么下列判断正确的有(填序号) .
①、abc>0, ②、b2-4ac<0, ③、2a+b>0, ④、a+b+c<0,
⑤、a-b+c>0,⑥、4a+2b+c<0,⑦、4a-2b+c<0.
①
③
⑦
2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,下列判断不正确的是( )
①、abc>0, ②、b2-4ac<0,
③、a-b+c<0, ④、4a+2b+c>0.
x
y
o
-1
2
3、二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系内的大致图象是( )
x
y
o
x
y
o
x
y
o
x
y
o
(C)
(D)
(B)
(A)
②
C
4、抛物线y=ax2+bx+c(a≠0)的图象
经过原点和二、三、四象限,判断
a、b、c的符号情况:
a 0,b 0,c 0.
x
y
o
<
=
<
5、抛物线y=ax2+bx+c(a≠0)的图象
经过原点,且它的顶点在第三象限,
则a、b、c满足的条件是:
a 0,b 0,c 0.
x
y
o
>
>
=
(a、b、c、△等符号)
X
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定:
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
(3)b的符号:
由对称轴的位置确定:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定:
抛物线与x轴有两个交点
b2-4ac>0
抛物线与x轴有一个交点
b2-4ac=0
抛 物 线 与 x 轴 无 交点
b2-4ac<0
归纳知识点:
简记为:左同右异
演示
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(5)a+b+c的符号:
由x=1时抛物线上的点的位置确定
(6)a-b+c的符号:
由x=-1时抛物线上的点的位置确定
利用以上知识主要解决以下几方面问题:
(1)由a,b,c,?的符号确定抛物线在坐标系中的大 致位置;
(2)由抛物线的位置确定系数a,b,c,?等符号及有
关a,b,c的代数式的符号;
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
练一练:
1.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )
A、第一象限
B、第二象限
C、第三象限
D、第四象限
x
o
y
D
练一练:
2、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个
x
o
y
x=1
B
练一练:
3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
4.如图,直线x= –1是二次函数
的图象的对称轴,则下列代数式abc,a+b+c,b2-4ac,2a-b,3a-b中负数有( )个
(A)1(B)2(C)3(D)4
练一练:
-2
二次函数y=ax2+bx+c(a≠0)的几个特例:
1、当x=1 时,
2、当x=-1时,
3、当x=2时,
4、当x=-2时,
y=a+b+c
y=a-b+c
y=4a+2b+c
y=4a-2b+c
…………… ……………
x
y
o
1
-1
2
练习:二次函数y=ax2+bx+c(a≠0)的图象如上图所示,那么下列判断正确的有(填序号) .
①、abc>0, ②、b2-4ac<0, ③、2a+b>0, ④、a+b+c<0,
⑤、a-b+c>0,⑥、4a+2b+c<0,⑦、4a-2b+c<0.
①
③
⑦
2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,下列判断不正确的是( )
①、abc>0, ②、b2-4ac<0,
③、a-b+c<0, ④、4a+2b+c>0.
x
y
o
-1
2
3、二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系内的大致图象是( )
x
y
o
x
y
o
x
y
o
x
y
o
(C)
(D)
(B)
(A)
②
C
4、抛物线y=ax2+bx+c(a≠0)的图象
经过原点和二、三、四象限,判断
a、b、c的符号情况:
a 0,b 0,c 0.
x
y
o
<
=
<
5、抛物线y=ax2+bx+c(a≠0)的图象
经过原点,且它的顶点在第三象限,
则a、b、c满足的条件是:
a 0,b 0,c 0.
x
y
o
>
>
=
