人教版八年级上册14.3.1因式分解—提公因式法课件(共30张ppt)
文档属性
| 名称 | 人教版八年级上册14.3.1因式分解—提公因式法课件(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 965.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览











文档简介
因式分解—提公因式法
复习引入
计算:
问题:
根据上面结果填空:
整式的乘积
多项式
多项式
整式的乘积
探究新知
像这样,把一个多项式化成几个整式的积的形式,这样的变形叫做这个多项式的因式分解,也叫把这个多项式分解因式.
因式分解
整式乘法
?
问题:
根据上面结果填空:
单项式、多项式乘积
单项式的和
因式分解
整式乘法
因式分解:
是把一个多项式化为了几个整式乘积的形式.
整式乘法:
是把几个整式乘积的形式化为多项式.
互为逆运算
练习:
下列变形中,属于因式分解变形的是_____(填序号)
分析:
(1)是由乘积形式转化为多项式,不属于因式分解.
(2)变形后仍为和的形式,不属于因式分解.
(3)(4)都由多项式转化成几个整式乘积形式,
属于因式分解.
√
√
×
×
(3)(4)
(1)a(b+c)=ab+ac (2)x3+2x2-3=x2(x+2)-3
(3)a2-b2=(a+b)(a-b) (4)a2-2a+1=(a-1)2
pa
探究新知
问题:
观察多项式pa+pb+pc,有什么特点吗?
pa+pb+pc
各项都有公共的因式p,我们把因式p叫做这个多项式的公因式.
我们发现:
pb
pc
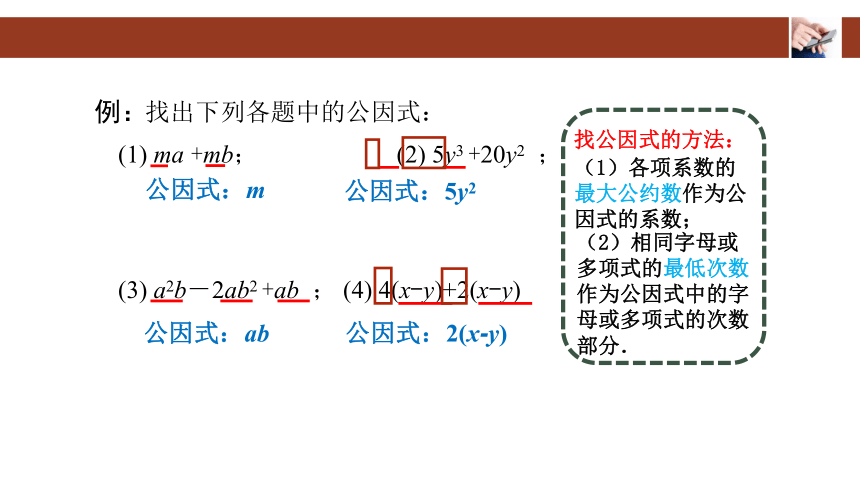
例:
找出下列各题中的公因式:
(1) ma +mb; (2) 5y3 +20y2 ;
(3) a2b-2ab2 +ab ; (4) 4(x-y)+2(x-y)
公因式:5y2
公因式:ab
找公因式的方法:
(1)各项系数的最大公约数作为公因式的系数;
(2)相同字母或多项式的最低次数作为公因式中的字母或多项式的次数部分.
公因式:m
公因式:2(x-y)
探究新知
问题:
你能尝试分解因式pa+pb+pc吗?
pa+pb+pc
因式分解的依据是什么?
根据分配律:
p(a+b+c)=pa+pb+pc
= p(a+b+c)
探究新知
问题:
分解后的各因式与原多项式有什么关系?
pa+pb+pc
= p (a+b+c)
公因式p
(pa+pb+pc) ÷p所得的商
提公因式法:
一般地,如果多项式中的各项有公因式,可以把公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解的方法叫做提公因式法.
例 把下列各式分解因式:
例 把下列各式分解因式:
公因式为4ab2
若提出公因式4ab,结果是什么?
例 把下列各式分解因式:
仍有公因式b,
未分解完!
需要继续分解!
例 把下列各式分解因式:
公因式为-2a
注意:不要丢掉+1这项!
法1:
=-(6a3+10a2+2a)
法2:
=-2a(3a2+5a+1)
=-2a(3a2+5a+1)
-6a3÷(-2a)=3a2
-10a2÷(-2a)=5a
-2a÷(-2a)=1
练习 把下列各式分解因式:
公因式为a2
公因式为-6b
a3÷a2=a
-a2b÷a2=-b
-12ab÷(-6b)=2a
6bc÷(-6b)=-c
公因式为5xy
公因式为ab
5x2y÷5xy=x
10xy2÷5xy=2y
-15xy÷5xy=-3
8a3b2÷ab=8a2b
-12ab3c÷ab=-12b2c
ab÷ab=1
例 把下列各式分解因式:
例 把下列各式分解因式:
分析:
通观察数字系数和字母,最大公因数为1,无相同字母.
解:
然而我们发现这两项中均有b+c,那么b+c可以看成一个整体,即为两项中的公因式,可以直接提出.
例 把下列各式分解因式:
分析:
解:(2)
我们发现b-3a和3a-b是互为相反数的关系,可先将其中一者稍加变形,再提出公因式.
(b-3a)2=[-(3a-b)]2=(3a-b)2
法一:
法二:
(b-3a)2-2(3a-b)
=(b-3a)2-2[-(b-3a)]
=(b-3a)2+2 (b-3a)
小结:
1.提公因式的方法:
一找:找公因式,即依次找系数的最大公约数、
相同字母及多项式的最小指数.
二提:提出公因式,用原式除以公因式得剩余
因式,分解后得公因式和剩余因式相乘.
小结:
2.提公因式需注意:
(1)首项系数为负数,要提出“-”号.
(2)某一项被整体提出后,剩余的项为1.
(3)各项有互为相反数的多项式,可把原式适当变形后提出公因式.
练习 下列因式分解正确的是( )
√
×
应为(a-b)(m+n)
原式变形为m(x-y)+n(x-y)
=(x-y)(m+n)
×
(x-y)[3(x-y)+2]
=(x-y)(3x-3y+2)
×
C
例 用简便方法计算:
解:
练习 分解因式:
解:
公因式为an
an÷an=1
-a3n÷an= -a3n-n=-a2n
an+2÷an= an+2-n=a2
想一想:我们今天学习了哪些知识?
归纳总结
1.因式分解:
把一个多项式化成了几个整式的积的形式,这样的式子变形叫做这个多项式的因式分解.
(2)因式分解 整式乘法
(1)因式分解本质:是将“和”转化为“积”的 变形.
注:
互逆运算
归纳总结
2.公因式:
多项式中各项都有的公共因式,叫做多项式各项的公因式.
3.因式分解的方法--提公因式法
(1) 找公因式
(2) 提公因式
计算:
拓展提升
.
解:
原式=
1.把下列各式分解因式:
2.先分解因式,再求值
课后作业
3.计算:
同学们,再见!
复习引入
计算:
问题:
根据上面结果填空:
整式的乘积
多项式
多项式
整式的乘积
探究新知
像这样,把一个多项式化成几个整式的积的形式,这样的变形叫做这个多项式的因式分解,也叫把这个多项式分解因式.
因式分解
整式乘法
?
问题:
根据上面结果填空:
单项式、多项式乘积
单项式的和
因式分解
整式乘法
因式分解:
是把一个多项式化为了几个整式乘积的形式.
整式乘法:
是把几个整式乘积的形式化为多项式.
互为逆运算
练习:
下列变形中,属于因式分解变形的是_____(填序号)
分析:
(1)是由乘积形式转化为多项式,不属于因式分解.
(2)变形后仍为和的形式,不属于因式分解.
(3)(4)都由多项式转化成几个整式乘积形式,
属于因式分解.
√
√
×
×
(3)(4)
(1)a(b+c)=ab+ac (2)x3+2x2-3=x2(x+2)-3
(3)a2-b2=(a+b)(a-b) (4)a2-2a+1=(a-1)2
pa
探究新知
问题:
观察多项式pa+pb+pc,有什么特点吗?
pa+pb+pc
各项都有公共的因式p,我们把因式p叫做这个多项式的公因式.
我们发现:
pb
pc
例:
找出下列各题中的公因式:
(1) ma +mb; (2) 5y3 +20y2 ;
(3) a2b-2ab2 +ab ; (4) 4(x-y)+2(x-y)
公因式:5y2
公因式:ab
找公因式的方法:
(1)各项系数的最大公约数作为公因式的系数;
(2)相同字母或多项式的最低次数作为公因式中的字母或多项式的次数部分.
公因式:m
公因式:2(x-y)
探究新知
问题:
你能尝试分解因式pa+pb+pc吗?
pa+pb+pc
因式分解的依据是什么?
根据分配律:
p(a+b+c)=pa+pb+pc
= p(a+b+c)
探究新知
问题:
分解后的各因式与原多项式有什么关系?
pa+pb+pc
= p (a+b+c)
公因式p
(pa+pb+pc) ÷p所得的商
提公因式法:
一般地,如果多项式中的各项有公因式,可以把公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解的方法叫做提公因式法.
例 把下列各式分解因式:
例 把下列各式分解因式:
公因式为4ab2
若提出公因式4ab,结果是什么?
例 把下列各式分解因式:
仍有公因式b,
未分解完!
需要继续分解!
例 把下列各式分解因式:
公因式为-2a
注意:不要丢掉+1这项!
法1:
=-(6a3+10a2+2a)
法2:
=-2a(3a2+5a+1)
=-2a(3a2+5a+1)
-6a3÷(-2a)=3a2
-10a2÷(-2a)=5a
-2a÷(-2a)=1
练习 把下列各式分解因式:
公因式为a2
公因式为-6b
a3÷a2=a
-a2b÷a2=-b
-12ab÷(-6b)=2a
6bc÷(-6b)=-c
公因式为5xy
公因式为ab
5x2y÷5xy=x
10xy2÷5xy=2y
-15xy÷5xy=-3
8a3b2÷ab=8a2b
-12ab3c÷ab=-12b2c
ab÷ab=1
例 把下列各式分解因式:
例 把下列各式分解因式:
分析:
通观察数字系数和字母,最大公因数为1,无相同字母.
解:
然而我们发现这两项中均有b+c,那么b+c可以看成一个整体,即为两项中的公因式,可以直接提出.
例 把下列各式分解因式:
分析:
解:(2)
我们发现b-3a和3a-b是互为相反数的关系,可先将其中一者稍加变形,再提出公因式.
(b-3a)2=[-(3a-b)]2=(3a-b)2
法一:
法二:
(b-3a)2-2(3a-b)
=(b-3a)2-2[-(b-3a)]
=(b-3a)2+2 (b-3a)
小结:
1.提公因式的方法:
一找:找公因式,即依次找系数的最大公约数、
相同字母及多项式的最小指数.
二提:提出公因式,用原式除以公因式得剩余
因式,分解后得公因式和剩余因式相乘.
小结:
2.提公因式需注意:
(1)首项系数为负数,要提出“-”号.
(2)某一项被整体提出后,剩余的项为1.
(3)各项有互为相反数的多项式,可把原式适当变形后提出公因式.
练习 下列因式分解正确的是( )
√
×
应为(a-b)(m+n)
原式变形为m(x-y)+n(x-y)
=(x-y)(m+n)
×
(x-y)[3(x-y)+2]
=(x-y)(3x-3y+2)
×
C
例 用简便方法计算:
解:
练习 分解因式:
解:
公因式为an
an÷an=1
-a3n÷an= -a3n-n=-a2n
an+2÷an= an+2-n=a2
想一想:我们今天学习了哪些知识?
归纳总结
1.因式分解:
把一个多项式化成了几个整式的积的形式,这样的式子变形叫做这个多项式的因式分解.
(2)因式分解 整式乘法
(1)因式分解本质:是将“和”转化为“积”的 变形.
注:
互逆运算
归纳总结
2.公因式:
多项式中各项都有的公共因式,叫做多项式各项的公因式.
3.因式分解的方法--提公因式法
(1) 找公因式
(2) 提公因式
计算:
拓展提升
.
解:
原式=
1.把下列各式分解因式:
2.先分解因式,再求值
课后作业
3.计算:
同学们,再见!
