人教版八年级数学下册20.2 数据的波动程度(1)(共32张ppt)
文档属性
| 名称 | 人教版八年级数学下册20.2 数据的波动程度(1)(共32张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 12:25:38 | ||
图片预览









文档简介
八年级 下册
20.2 数据的波动程度(1)
学习目标:
1.经历方差的形成过程,了解方差的意义;
2.掌握方差的计算方法并会初步运用方差解决实际
问题.
学习重点:
方差意义的理解及应用.
新课填补:
何谓一组数据的极差?
极差反映了这组数据哪方面的特征?
答 一组数据中的最大值减去最小值所得的差叫做这组数据的极差。
极差反映的是这组数据的变化范围或变化幅度,也称离散程度
极差只能反映一组数据中两个极值之间的大小情况,而对其他数据的波动情况不敏感。
乒乓球的标准直径为40mm,质检部门从A、B两厂生产的乒乓球中各抽取了10只,对这些乒乓球的直径了进行检测。结果如下(单位:mm):
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:39.8,40.2,39.8,40.2,39.9,
40.1,39.8,40.2,39.8,40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢?
请你算一算它们的平均数和极差。
是否由此就断定两厂生产的乒乓球直径同样标准?
今天我们一起来探索这个问题。
情境一:
甲,乙两名射击手都很优秀,现只能挑选一名射击手参加比赛.
若你是教练,你认为挑选哪一位比较适宜?
教练的烦恼
?
情境二:
第一次
第二次
第三次
第四次
第五次
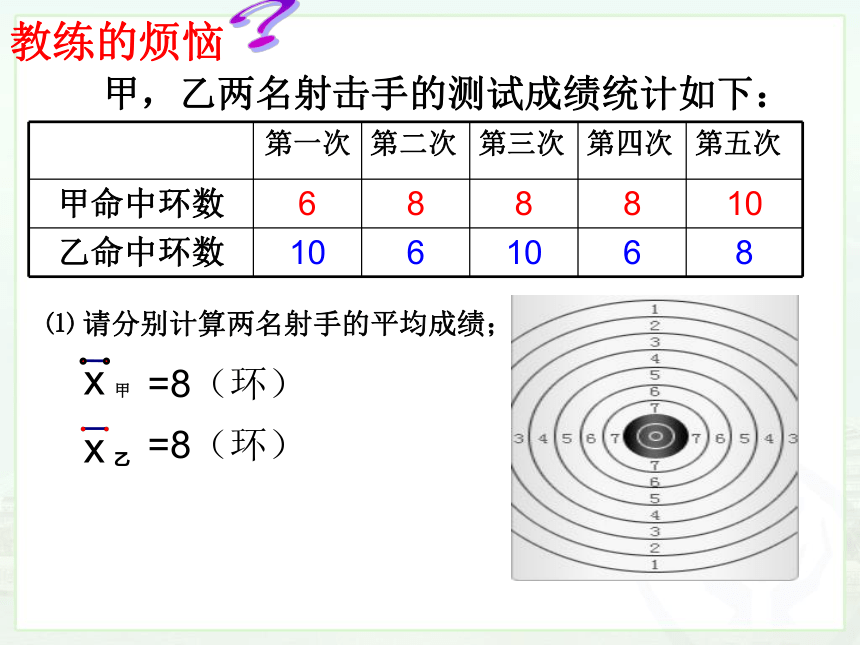
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
甲,乙两名射击手的测试成绩统计如下:
⑴ 请分别计算两名射手的平均成绩;
教练的烦恼
?
=8(环)
=8(环)
甲
x
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在
下图中画出折线统计图;
教练的烦恼
?
他们的极差分别是多少?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在
下图中画出折线统计图;
教练的烦恼
?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在
下图中画出折线统计图;
⑶ 现要挑选一名射击手参加比
赛,若你是教练,你认为挑
选哪一位比较适宜?为什么?
教练的烦恼
?
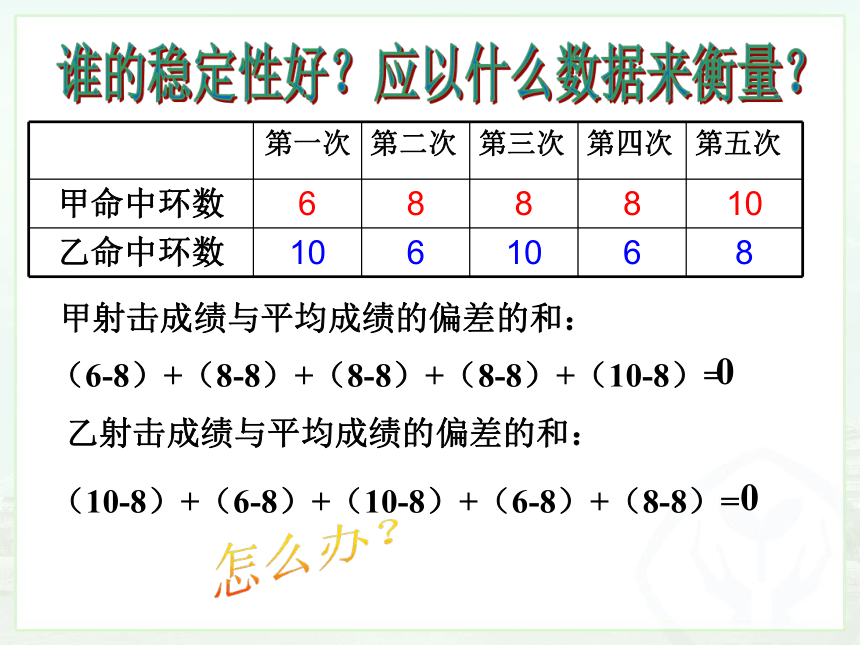
谁的稳定性好?应以什么数据来衡量?
甲射击成绩与平均成绩的偏差的和:
乙射击成绩与平均成绩的偏差的和:
(6-8)+(8-8)+(8-8)+(8-8)+(10-8)=
0
(10-8)+(6-8)+(10-8)+(6-8)+(8-8)=
0
怎么办?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
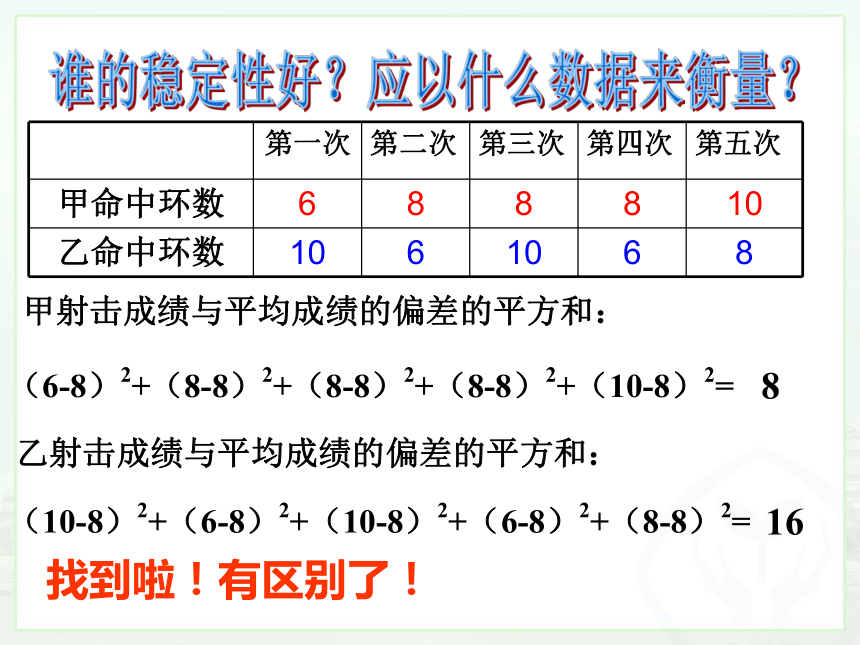
谁的稳定性好?应以什么数据来衡量?
(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=
(6-8)2+(8-8)2+(8-8)2+(8-8)2+(10-8)2=
甲射击成绩与平均成绩的偏差的平方和:
乙射击成绩与平均成绩的偏差的平方和:
找到啦!有区别了!
8
16
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
想一想
上述各偏差的平方和的大小还与什么有关?
——与射击次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2 、… (xn-x)2 ,那么我们用它们的平均数,即用
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差的定义:
我们采用各偏差平方的平均数来衡量数据的稳定性,
即
叫做这组数据的方差(用S2来表示)。
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
谁的稳定性好?应以什么数据来衡量?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
试一试计算甲,乙两组数据的方差
由方差的定义,要注意:
1、方差是衡量数据稳定性的一个统计量;
2、要求某组数据的方差,要先求数据的平均数;
3、方差的单位是所给数据单位的平方;
4、方差越大,波动越大,越不稳定;
方差越小,波动越小,越稳定。
例题精选
例 为了考察甲乙两种小麦的长势,分别从中
抽出10株苗,测得苗高如下(单位:cm):
甲:12,13,14,15,10,16,13,11,15,11;
乙:11,16,17,14,13,19, 6, 8,10,16;
问:哪种小麦长得比较整齐?
X甲= ( cm)
X乙= (cm)
S2甲= (cm2)
S2乙= (cm2)
因为S2甲< S2乙,所以甲种小麦长得比较整齐。
解:
乒乓球的标准直径为40mm,质检部门从A、B两厂生产的乒乓球中各抽取了10只,对这些乒乓球的直径了进行检测。结果如下(单位:mm):
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:39.8,40.2,39.8,40.2,39.9,
40.1,39.8,40.2,39.8,40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢?
现在可以判断了吗?试试看。
小试牛刀:
标准差的定义
为了使得与数据单位一致,可用方差的
算术平方根来表示(即标准差):
,S为标准差。
特殊的:如果方差与标准差为零,说明数据
都没有偏差,即每个数都一样 。
一般来说,一组数据的方差或标准差越小,这组数据离散程度越小,这组数据就越稳定。
练习:
1.若甲组数据的方差比乙组数据的方差大,那
么下列说法正确的是( )
A.甲组数据的平均数比乙组数据的平均数大
B.甲组数据比乙组数据稳定
C.乙组数据比甲组数据稳定
D.甲,乙组的稳定性不能确定
C
练习:
2.一组数据的7、8 、9 、10 、11 、12 、13
的方差是______.标准差是______.
3.已知一组数据-1,x,0,1,-2的平均数
是0,那么这组数据的方差是______.
反映数据离散程度的指标是什么?在一次数学测试中,甲、乙两班的平均成绩相同,甲班成绩的方差为42,乙班成绩的方差为35,这样的结果说明两个班的数学学习状况各有什么特点?
谈谈自己这节课你学到了什么?
1.方差:各数据与平均数的差的平方的平均
数叫做这批数据的方差.
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
小结:
2.方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
在样本容量相同的情况下:
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定.
3.极差、方差的区别与联系
方差是用“先平均,再求差,然后平方,最后再平均”的方法得到的结果,主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数据的变化都将影响方差的结果,是一个对整组数据波动情况更敏感的指标。
区别:
极差是用一组数据中的最大值与最小值的差来反映数据的变化范围,主要反映一组数据中两个极端值之间的差异情况,对其他的数据的波动不敏感。
极差、方差都是用来衡量(或描述)一组数据偏离平均数的大小(即波动大小)的指标,常用来比较两组数据的波动情况。
在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小。
联系:
为什么常用方差来衡量一组数据的波动情况呢?有兴趣的同学可以参考本节的“阅读与思考数据波动的几种度量”
1.用条形图表示下列各数,计算并比较
它们的平均数和方差,体会方差是怎样
刻画数据的波动程度的
(1) 6 6 6 6 6 6 6
(2) 5 5 6 6 6 7 7
(3) 3 3 4 6 8 9 9
(4) 3 3 3 6 9 9 9
练习
1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的。
(1)6 6 6 6 6 6 6
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
2、下面是两名跳远运动员的10次测验成绩(单位:m)
甲
5.85
5.93
6.07
5.91
5.99
6.13
5.98
6.05
6.00
6.19
乙
6.11
6.08
5.83
5.92
5.84
5.81
6.18
6.17
5.85
6.21
在这10次测验中,哪名运动员的成绩更稳定?(可以使用计算器)
20.2 数据的波动程度(1)
学习目标:
1.经历方差的形成过程,了解方差的意义;
2.掌握方差的计算方法并会初步运用方差解决实际
问题.
学习重点:
方差意义的理解及应用.
新课填补:
何谓一组数据的极差?
极差反映了这组数据哪方面的特征?
答 一组数据中的最大值减去最小值所得的差叫做这组数据的极差。
极差反映的是这组数据的变化范围或变化幅度,也称离散程度
极差只能反映一组数据中两个极值之间的大小情况,而对其他数据的波动情况不敏感。
乒乓球的标准直径为40mm,质检部门从A、B两厂生产的乒乓球中各抽取了10只,对这些乒乓球的直径了进行检测。结果如下(单位:mm):
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:39.8,40.2,39.8,40.2,39.9,
40.1,39.8,40.2,39.8,40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢?
请你算一算它们的平均数和极差。
是否由此就断定两厂生产的乒乓球直径同样标准?
今天我们一起来探索这个问题。
情境一:
甲,乙两名射击手都很优秀,现只能挑选一名射击手参加比赛.
若你是教练,你认为挑选哪一位比较适宜?
教练的烦恼
?
情境二:
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
甲,乙两名射击手的测试成绩统计如下:
⑴ 请分别计算两名射手的平均成绩;
教练的烦恼
?
=8(环)
=8(环)
甲
x
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在
下图中画出折线统计图;
教练的烦恼
?
他们的极差分别是多少?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在
下图中画出折线统计图;
教练的烦恼
?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在
下图中画出折线统计图;
⑶ 现要挑选一名射击手参加比
赛,若你是教练,你认为挑
选哪一位比较适宜?为什么?
教练的烦恼
?
谁的稳定性好?应以什么数据来衡量?
甲射击成绩与平均成绩的偏差的和:
乙射击成绩与平均成绩的偏差的和:
(6-8)+(8-8)+(8-8)+(8-8)+(10-8)=
0
(10-8)+(6-8)+(10-8)+(6-8)+(8-8)=
0
怎么办?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
谁的稳定性好?应以什么数据来衡量?
(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=
(6-8)2+(8-8)2+(8-8)2+(8-8)2+(10-8)2=
甲射击成绩与平均成绩的偏差的平方和:
乙射击成绩与平均成绩的偏差的平方和:
找到啦!有区别了!
8
16
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
想一想
上述各偏差的平方和的大小还与什么有关?
——与射击次数有关!
所以要进一步用各偏差平方的平均数来衡量数据的稳定性
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2 、… (xn-x)2 ,那么我们用它们的平均数,即用
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差的定义:
我们采用各偏差平方的平均数来衡量数据的稳定性,
即
叫做这组数据的方差(用S2来表示)。
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
谁的稳定性好?应以什么数据来衡量?
第一次
第二次
第三次
第四次
第五次
甲命中环数
6
8
8
8
10
乙命中环数
10
6
10
6
8
试一试计算甲,乙两组数据的方差
由方差的定义,要注意:
1、方差是衡量数据稳定性的一个统计量;
2、要求某组数据的方差,要先求数据的平均数;
3、方差的单位是所给数据单位的平方;
4、方差越大,波动越大,越不稳定;
方差越小,波动越小,越稳定。
例题精选
例 为了考察甲乙两种小麦的长势,分别从中
抽出10株苗,测得苗高如下(单位:cm):
甲:12,13,14,15,10,16,13,11,15,11;
乙:11,16,17,14,13,19, 6, 8,10,16;
问:哪种小麦长得比较整齐?
X甲= ( cm)
X乙= (cm)
S2甲= (cm2)
S2乙= (cm2)
因为S2甲< S2乙,所以甲种小麦长得比较整齐。
解:
乒乓球的标准直径为40mm,质检部门从A、B两厂生产的乒乓球中各抽取了10只,对这些乒乓球的直径了进行检测。结果如下(单位:mm):
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:39.8,40.2,39.8,40.2,39.9,
40.1,39.8,40.2,39.8,40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢?
现在可以判断了吗?试试看。
小试牛刀:
标准差的定义
为了使得与数据单位一致,可用方差的
算术平方根来表示(即标准差):
,S为标准差。
特殊的:如果方差与标准差为零,说明数据
都没有偏差,即每个数都一样 。
一般来说,一组数据的方差或标准差越小,这组数据离散程度越小,这组数据就越稳定。
练习:
1.若甲组数据的方差比乙组数据的方差大,那
么下列说法正确的是( )
A.甲组数据的平均数比乙组数据的平均数大
B.甲组数据比乙组数据稳定
C.乙组数据比甲组数据稳定
D.甲,乙组的稳定性不能确定
C
练习:
2.一组数据的7、8 、9 、10 、11 、12 、13
的方差是______.标准差是______.
3.已知一组数据-1,x,0,1,-2的平均数
是0,那么这组数据的方差是______.
反映数据离散程度的指标是什么?在一次数学测试中,甲、乙两班的平均成绩相同,甲班成绩的方差为42,乙班成绩的方差为35,这样的结果说明两个班的数学学习状况各有什么特点?
谈谈自己这节课你学到了什么?
1.方差:各数据与平均数的差的平方的平均
数叫做这批数据的方差.
S2= [ (x1-x)2+(x2-x)2+ +(xn-x)2 ]
小结:
2.方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
在样本容量相同的情况下:
方差越大,说明数据的波动越大,越不稳定.
方差越小,说明数据的波动越小,越稳定.
3.极差、方差的区别与联系
方差是用“先平均,再求差,然后平方,最后再平均”的方法得到的结果,主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数据的变化都将影响方差的结果,是一个对整组数据波动情况更敏感的指标。
区别:
极差是用一组数据中的最大值与最小值的差来反映数据的变化范围,主要反映一组数据中两个极端值之间的差异情况,对其他的数据的波动不敏感。
极差、方差都是用来衡量(或描述)一组数据偏离平均数的大小(即波动大小)的指标,常用来比较两组数据的波动情况。
在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小。
联系:
为什么常用方差来衡量一组数据的波动情况呢?有兴趣的同学可以参考本节的“阅读与思考数据波动的几种度量”
1.用条形图表示下列各数,计算并比较
它们的平均数和方差,体会方差是怎样
刻画数据的波动程度的
(1) 6 6 6 6 6 6 6
(2) 5 5 6 6 6 7 7
(3) 3 3 4 6 8 9 9
(4) 3 3 3 6 9 9 9
练习
1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的。
(1)6 6 6 6 6 6 6
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
2、下面是两名跳远运动员的10次测验成绩(单位:m)
甲
5.85
5.93
6.07
5.91
5.99
6.13
5.98
6.05
6.00
6.19
乙
6.11
6.08
5.83
5.92
5.84
5.81
6.18
6.17
5.85
6.21
在这10次测验中,哪名运动员的成绩更稳定?(可以使用计算器)
