人教版八年级下数学18.1.1平行四边形的性质——平行四边形对角线互相平分(共17张ppt)
文档属性
| 名称 | 人教版八年级下数学18.1.1平行四边形的性质——平行四边形对角线互相平分(共17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 12:32:47 | ||
图片预览



文档简介
人教版义务教育教科书
八年级下册第十八章第一节第二课时
《平行四边形的性质(二)》
A
B
D
C
文字语言
图形语言
符号语言
平行四边形ABCD
ABCD
定义
文字语言:
符号
语言:
性质
边
位置关系
文字:
符号:
数量关系
文字:
符号:
角
对角
文字:
符号:
邻角
文字:
符
号:
…
…
…
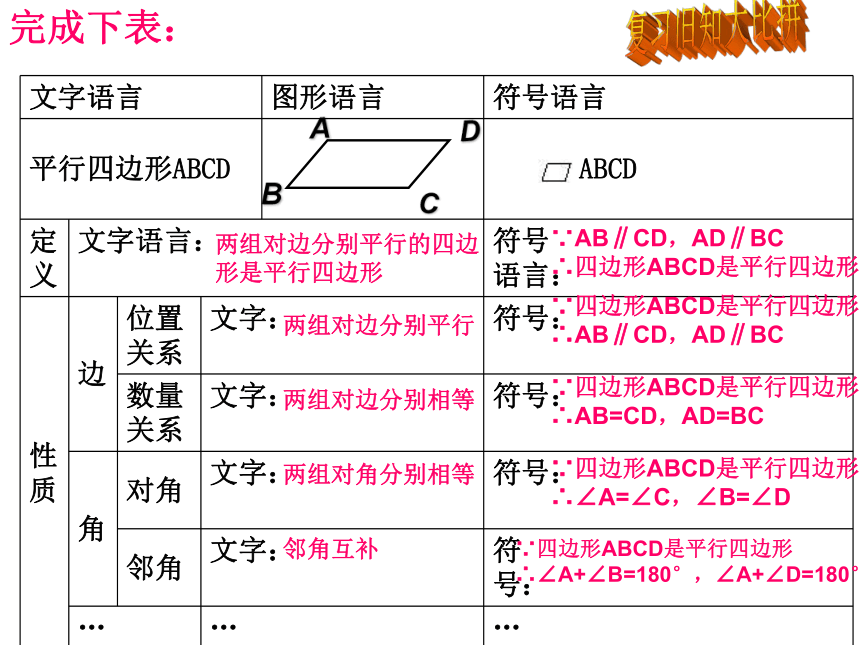
完成下表:
两组对边分别平行的四边
形是平行四边形
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别平行
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
两组对边分别相等
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
两组对角分别相等
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
邻角互补
∵四边形ABCD是平行四边形
∴∠A+∠B=180°,∠A+∠D=180°
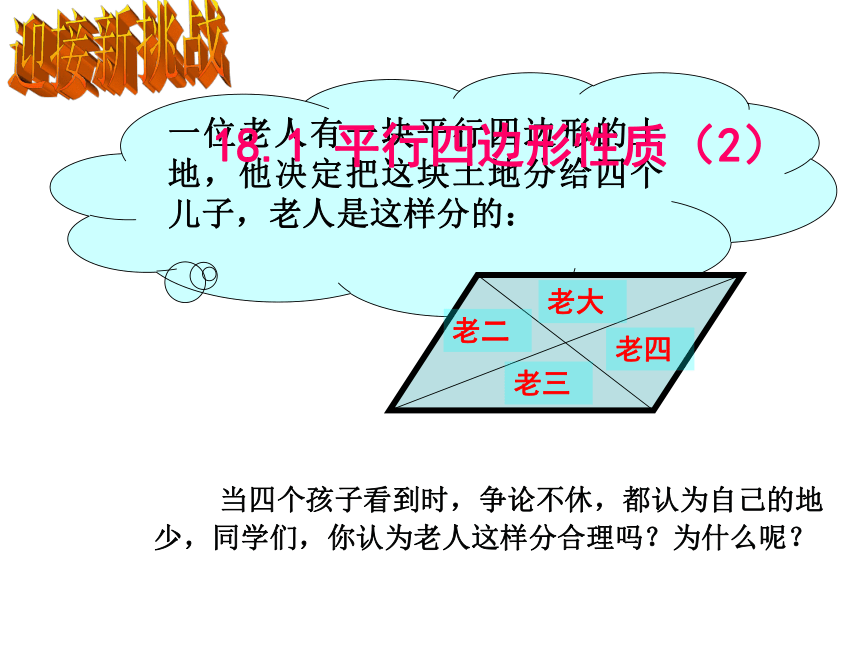
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么呢?
一位老人有一块平行四边形的土地,他决定把这块土地分给四个儿子,老人是这样分的:
老大
老三
老四
老二
18.1
平行四边形性质(2)
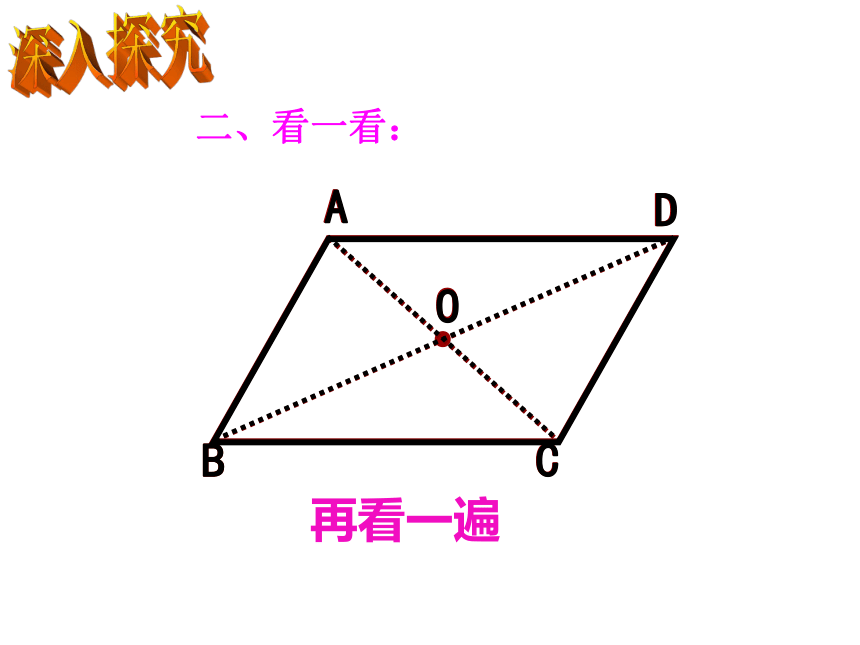
问题:(1)你能观察到平行四边形的对角线有哪些关系吗?
A
B
D
C
O
(2)这些猜想,都是正确的吗?你能通过动手操作验证吗?
如图,平行四边形ABCD的两条对角线AC、BD相交于点O.
●
A
D
O
C
B
D
B
O
C
A
再看一遍
二、看一看:
●
A
D
O
C
B
D
B
O
C
A
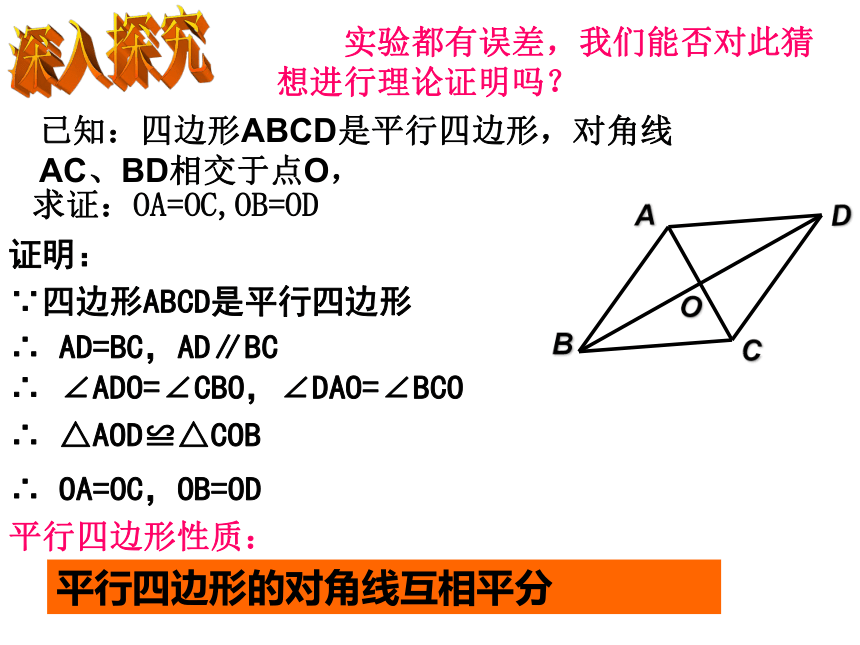
实验都有误差,我们能否对此猜想进行理论证明吗?
A
B
D
C
O
平行四边形的对角线互相平分
求证:OA=OC,OB=OD
∵四边形ABCD是平行四边形
∴
AD=BC,AD∥BC
∴
∠ADO=∠CBO,∠DAO=∠BCO
∴
△AOD≌△COB
∴
OA=OC,OB=OD
平行四边形性质:
已知:四边形ABCD是平行四边形,对角线AC、BD相交于点O,
证明:
1、试一试:
(1)如图1,在
ABCD中,AC=8,BD=10,则
AO=____;BO=_____;CO=____;DO=_____。
(2)如图1,
ABCD中,对角线AC、BD相交于点
O,已知AC+BD=20,则CO+DO=___;若AB=8,
则△COD的周长____。
A
B
D
C
O
图1
4
5
4
5
10
18
1、如图2,在平行四边形ABCD中,AC、BD相
交于点O
,那么图中有_______组全等三角形。
A
E
A
B
D
C
O
图2
4
△ABC
△ABD
△AOB
△AOD
≌△CDA
≌△CDB
≌△COD
≌△COB
A
C
D
B
O
●
老大
老四
老三
老二
M
例1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC.
B
C
D
A
O
10
8
8
10
8
10
问题1:根据这些条件你能求出哪些线段的长?
问题2:求出这些线段后,你还能得到什么?
4、变式:如上图,将“AC⊥BC”改成“
OA=3”,其余条件不变,那么你能求出哪些线段的长?哪些角的度数?还能进一步求出什么?
B
C
D
A
O
10
8
6
?
10
8
5、如图4,
ABCD的对角线AC、BD相交于点O,直线EF过点O且与AB,CD分别相交于点E、F。你又可以得到什么结论?
A
E
E
F
●
O
D
C
B
A
图4
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
1.
我们学行四边形的哪些性质?
A
E
平行四边形的性质
边
角
对角线
位置关系:
两组对边分别平行
数量关系:
两组对边分别相等
对角:
两组对角分别相等
邻角:
邻角互补
对角线互相平分
2.结合本节课的学习,谈谈研究平行四边形性质的
思想方法。
1、必做题:教材第49页第3题
2、选做题:如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别在OB、OD上,当点E、F满足什么条件时,AE=CF?
A
E
E
●
O
D
C
B
A
F
八年级下册第十八章第一节第二课时
《平行四边形的性质(二)》
A
B
D
C
文字语言
图形语言
符号语言
平行四边形ABCD
ABCD
定义
文字语言:
符号
语言:
性质
边
位置关系
文字:
符号:
数量关系
文字:
符号:
角
对角
文字:
符号:
邻角
文字:
符
号:
…
…
…
完成下表:
两组对边分别平行的四边
形是平行四边形
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别平行
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
两组对边分别相等
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
两组对角分别相等
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
邻角互补
∵四边形ABCD是平行四边形
∴∠A+∠B=180°,∠A+∠D=180°
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么呢?
一位老人有一块平行四边形的土地,他决定把这块土地分给四个儿子,老人是这样分的:
老大
老三
老四
老二
18.1
平行四边形性质(2)
问题:(1)你能观察到平行四边形的对角线有哪些关系吗?
A
B
D
C
O
(2)这些猜想,都是正确的吗?你能通过动手操作验证吗?
如图,平行四边形ABCD的两条对角线AC、BD相交于点O.
●
A
D
O
C
B
D
B
O
C
A
再看一遍
二、看一看:
●
A
D
O
C
B
D
B
O
C
A
实验都有误差,我们能否对此猜想进行理论证明吗?
A
B
D
C
O
平行四边形的对角线互相平分
求证:OA=OC,OB=OD
∵四边形ABCD是平行四边形
∴
AD=BC,AD∥BC
∴
∠ADO=∠CBO,∠DAO=∠BCO
∴
△AOD≌△COB
∴
OA=OC,OB=OD
平行四边形性质:
已知:四边形ABCD是平行四边形,对角线AC、BD相交于点O,
证明:
1、试一试:
(1)如图1,在
ABCD中,AC=8,BD=10,则
AO=____;BO=_____;CO=____;DO=_____。
(2)如图1,
ABCD中,对角线AC、BD相交于点
O,已知AC+BD=20,则CO+DO=___;若AB=8,
则△COD的周长____。
A
B
D
C
O
图1
4
5
4
5
10
18
1、如图2,在平行四边形ABCD中,AC、BD相
交于点O
,那么图中有_______组全等三角形。
A
E
A
B
D
C
O
图2
4
△ABC
△ABD
△AOB
△AOD
≌△CDA
≌△CDB
≌△COD
≌△COB
A
C
D
B
O
●
老大
老四
老三
老二
M
例1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC.
B
C
D
A
O
10
8
8
10
8
10
问题1:根据这些条件你能求出哪些线段的长?
问题2:求出这些线段后,你还能得到什么?
4、变式:如上图,将“AC⊥BC”改成“
OA=3”,其余条件不变,那么你能求出哪些线段的长?哪些角的度数?还能进一步求出什么?
B
C
D
A
O
10
8
6
?
10
8
5、如图4,
ABCD的对角线AC、BD相交于点O,直线EF过点O且与AB,CD分别相交于点E、F。你又可以得到什么结论?
A
E
E
F
●
O
D
C
B
A
图4
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
1.
我们学行四边形的哪些性质?
A
E
平行四边形的性质
边
角
对角线
位置关系:
两组对边分别平行
数量关系:
两组对边分别相等
对角:
两组对角分别相等
邻角:
邻角互补
对角线互相平分
2.结合本节课的学习,谈谈研究平行四边形性质的
思想方法。
1、必做题:教材第49页第3题
2、选做题:如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别在OB、OD上,当点E、F满足什么条件时,AE=CF?
A
E
E
●
O
D
C
B
A
F
