人教版七年级数学下册 5.2.2:平行线的判定(共17张ppt)
文档属性
| 名称 | 人教版七年级数学下册 5.2.2:平行线的判定(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
5.2.2 平行线的判定
知识回顾
问题1 两条不重合的直线的位置关系有哪几种
问题2 平行公理
问题3 怎样判定两条直线平行
相交(包括垂直)和平行两种.
经过直线外一点,有且只有一条直线与已知直线平行.
问题4 有没有其他的判定两直线互相平行的方法
(1)平行的定义:在同一平面内,不相交的两条直线互相平行;
(2)推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行(传递性);
动手操作
动手画一画:画两条平行线
问题1: ∠1和∠2有怎样的位置关系
同位角
相等
一放
二靠
·
1
)
)
2
三推
四画
问题2:∠1与∠2相等吗
只要同位角相等,两直线就平行.
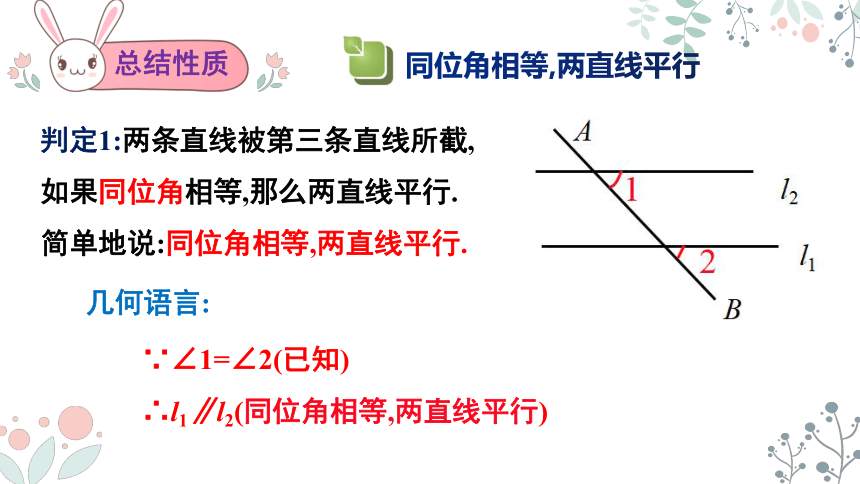
总结性质
几何语言:
判定1:两条直线被第三条直线所截,
如果同位角相等,那么两直线平行.
简单地说:同位角相等,两直线平行.
∵∠1=∠2(已知)
∴l1∥l2(同位角相等,两直线平行)
同位角相等,两直线平行
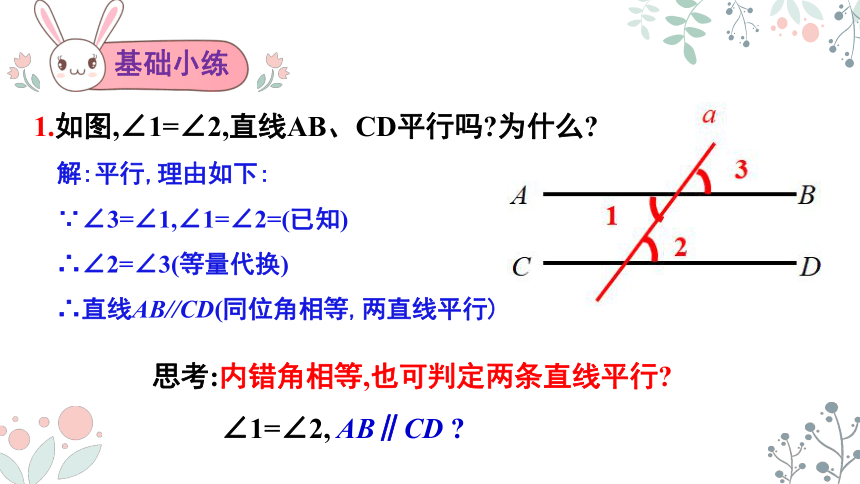
基础小练
1.如图,∠1=∠2,直线AB、CD平行吗 为什么
解:平行,理由如下:
∵∠3=∠1,∠1=∠2=(已知)
∴∠2=∠3(等量代换)
∴直线AB//CD(同位角相等,两直线平行)
思考:内错角相等,也可判定两条直线平行
∠1=∠2, AB∥CD
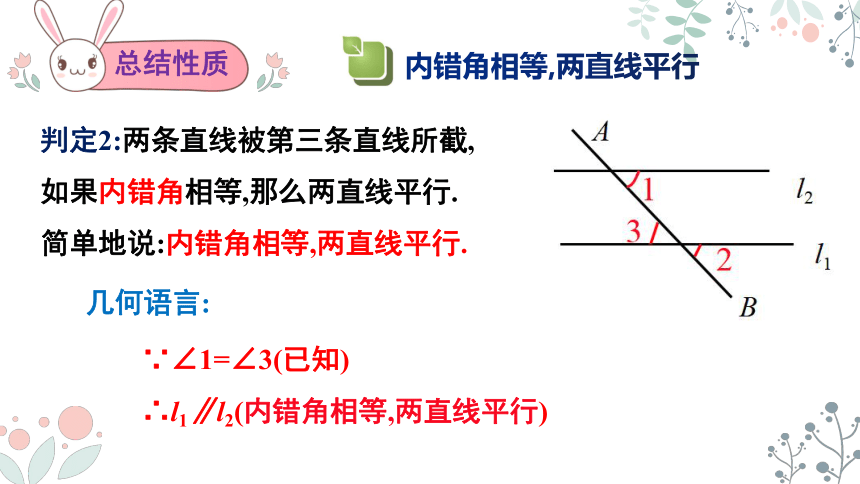
总结性质
几何语言:
判定2:两条直线被第三条直线所截,
如果内错角相等,那么两直线平行.
简单地说:内错角相等,两直线平行.
∵∠1=∠3(已知)
∴l1∥l2(内错角相等,两直线平行)
内错角相等,两直线平行
基础小练
2.如图,如果 1=55°, 2=125° ,直线a//直线b吗 为什么
解:直线a//直线b, 理由如下
∵ 1=55°(已知)
∴ 3=180°-∠1=180°-55°=125°(邻补角定义)
又∵ 2=125°(已知) 2= 3(等量代换)
a//b (同位角相等,两直线平行)
思考:同旁内角互补,也可判定两条直线平行
即: ∠1+∠2=180°, a∥b 成立
总结性质
几何语言:
判定3:两条直线被第三条直线所截,
如果同旁内角互补,那么两直线平行.
简单地说:同旁内角互补,两直线平行.
∵∠1+∠4=180°(已知)
∴l1∥l2(同旁内角互补,两直线平行)
同旁内角互补,两直线平行
总结性质
3
同旁内角互补,两直线平行
直线平行的判定
数量关系
位置关系
1
同位角相等,两直线平行
2
内错角相等,两直线平行
基础小练
3.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A C. ∠3=∠B D. ∠3=∠A
4.下列图形中,由∠1=∠2能得到AB∥CD的是( )
5.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
基础小练
6.如图,BE是AB的延长线.
(1)由∠CBE=∠A,可以判断哪两条直线平行 根据是什么
(2)由∠CBE=∠C,可以判断哪两条直线平行 根据是什么
(3)由∠A+∠D=180°,可以判断哪两条直线平行 根据是什么
基础小练
7.如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)∵∠B=∠DCG
∴___ // ___(_____________)
(2)∵∠D=∠DCG
∴___ // ___(_____________)
(3)∵∠D+∠DFE=180°
∴___ // ___(_____________)
典例分析
例 在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗 为什么
结论:在同一平面内,垂直于同一直线的两直线互相平行
提示:垂直总与直角联系在一起,进而用判断 两条直线平行的方法进行判定.
解:这两条直线平行. 理由如下:
如图.∵a⊥b,∴∠1=90°.
同理∠2=90°.∴∠1=∠2 .
∵ ∠1和∠2 是同位角,∴b∥c (同位角相等,两直线平行).
基础小练
8.判定两条直线平行有几种方法
9.如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行 请说明理由
拓展提升
10.根据条件完成填空.
① ∵ ∠1 =_____(已知),∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),∴ CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),∴ _____∥_____( ).
④ ∵ ∠4 +_____=180o(已知),∴ CE∥AB( ).
(1)从∠1=∠4,可以推出 ∥ ,理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,理由是 .
(3)从∠ =∠ ,可以推出AD∥BC,理由是 .
(4)从∠5=∠ ,可以推出AB∥CD,理由是 .
拓展提升
11.如图:若∠B+ ∠D=∠BED,试说明AB//CD.
文字叙述 符号语言 图形
______,两直线平行 ∵______(已知),∴a∥b
______,两直线平行 ∵______(已知),∴a∥b _______, 两直线平行 ∵________(已知)∴a∥b 课堂小结
判定两条直线平行的方法
同一平面内,垂直于同一条直线的两条直线平行.
∵ b⊥a,c⊥a(已知)∴b∥c
同位角相等
内错角相等
∠1=∠2
∠3=∠2
∠2+∠4=180°
同旁内角互补
5.2.2 平行线的判定
知识回顾
问题1 两条不重合的直线的位置关系有哪几种
问题2 平行公理
问题3 怎样判定两条直线平行
相交(包括垂直)和平行两种.
经过直线外一点,有且只有一条直线与已知直线平行.
问题4 有没有其他的判定两直线互相平行的方法
(1)平行的定义:在同一平面内,不相交的两条直线互相平行;
(2)推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行(传递性);
动手操作
动手画一画:画两条平行线
问题1: ∠1和∠2有怎样的位置关系
同位角
相等
一放
二靠
·
1
)
)
2
三推
四画
问题2:∠1与∠2相等吗
只要同位角相等,两直线就平行.
总结性质
几何语言:
判定1:两条直线被第三条直线所截,
如果同位角相等,那么两直线平行.
简单地说:同位角相等,两直线平行.
∵∠1=∠2(已知)
∴l1∥l2(同位角相等,两直线平行)
同位角相等,两直线平行
基础小练
1.如图,∠1=∠2,直线AB、CD平行吗 为什么
解:平行,理由如下:
∵∠3=∠1,∠1=∠2=(已知)
∴∠2=∠3(等量代换)
∴直线AB//CD(同位角相等,两直线平行)
思考:内错角相等,也可判定两条直线平行
∠1=∠2, AB∥CD
总结性质
几何语言:
判定2:两条直线被第三条直线所截,
如果内错角相等,那么两直线平行.
简单地说:内错角相等,两直线平行.
∵∠1=∠3(已知)
∴l1∥l2(内错角相等,两直线平行)
内错角相等,两直线平行
基础小练
2.如图,如果 1=55°, 2=125° ,直线a//直线b吗 为什么
解:直线a//直线b, 理由如下
∵ 1=55°(已知)
∴ 3=180°-∠1=180°-55°=125°(邻补角定义)
又∵ 2=125°(已知) 2= 3(等量代换)
a//b (同位角相等,两直线平行)
思考:同旁内角互补,也可判定两条直线平行
即: ∠1+∠2=180°, a∥b 成立
总结性质
几何语言:
判定3:两条直线被第三条直线所截,
如果同旁内角互补,那么两直线平行.
简单地说:同旁内角互补,两直线平行.
∵∠1+∠4=180°(已知)
∴l1∥l2(同旁内角互补,两直线平行)
同旁内角互补,两直线平行
总结性质
3
同旁内角互补,两直线平行
直线平行的判定
数量关系
位置关系
1
同位角相等,两直线平行
2
内错角相等,两直线平行
基础小练
3.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A C. ∠3=∠B D. ∠3=∠A
4.下列图形中,由∠1=∠2能得到AB∥CD的是( )
5.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
基础小练
6.如图,BE是AB的延长线.
(1)由∠CBE=∠A,可以判断哪两条直线平行 根据是什么
(2)由∠CBE=∠C,可以判断哪两条直线平行 根据是什么
(3)由∠A+∠D=180°,可以判断哪两条直线平行 根据是什么
基础小练
7.如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)∵∠B=∠DCG
∴___ // ___(_____________)
(2)∵∠D=∠DCG
∴___ // ___(_____________)
(3)∵∠D+∠DFE=180°
∴___ // ___(_____________)
典例分析
例 在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗 为什么
结论:在同一平面内,垂直于同一直线的两直线互相平行
提示:垂直总与直角联系在一起,进而用判断 两条直线平行的方法进行判定.
解:这两条直线平行. 理由如下:
如图.∵a⊥b,∴∠1=90°.
同理∠2=90°.∴∠1=∠2 .
∵ ∠1和∠2 是同位角,∴b∥c (同位角相等,两直线平行).
基础小练
8.判定两条直线平行有几种方法
9.如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行 请说明理由
拓展提升
10.根据条件完成填空.
① ∵ ∠1 =_____(已知),∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),∴ CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),∴ _____∥_____( ).
④ ∵ ∠4 +_____=180o(已知),∴ CE∥AB( ).
(1)从∠1=∠4,可以推出 ∥ ,理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,理由是 .
(3)从∠ =∠ ,可以推出AD∥BC,理由是 .
(4)从∠5=∠ ,可以推出AB∥CD,理由是 .
拓展提升
11.如图:若∠B+ ∠D=∠BED,试说明AB//CD.
文字叙述 符号语言 图形
______,两直线平行 ∵______(已知),∴a∥b
______,两直线平行 ∵______(已知),∴a∥b _______, 两直线平行 ∵________(已知)∴a∥b 课堂小结
判定两条直线平行的方法
同一平面内,垂直于同一条直线的两条直线平行.
∵ b⊥a,c⊥a(已知)∴b∥c
同位角相等
内错角相等
∠1=∠2
∠3=∠2
∠2+∠4=180°
同旁内角互补
