人教版七年级下册5.2.2平行线的判定课件(共17张ppt)
文档属性
| 名称 | 人教版七年级下册5.2.2平行线的判定课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 389.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览



文档简介
5.2.2平行线的判定
学习目标:
1、运用平行线的画法对平行线的判定方法1进行推导;
2、分析并推导平行线的判定方法2、3、4,并对平行线判定的6种方法进行概括总结;
3、会正确运用平行线的判定方法对两条直线的位置关系进行判定即平行线判定的简单运用;
一、知识回顾
1、两条直线的位置关系有哪几种?
3、怎样判定两条直线平行?
2、平行线的公理是什么?
相交和平行
1)平行的定义:在同一平面内,不相交的两条直线互相平行;
2)推论:如果两条直线都和第三条直线平行,那么这两
条直线也互相平行(传递性);
问题:有没有其他的判定两直线互相平行的方法?
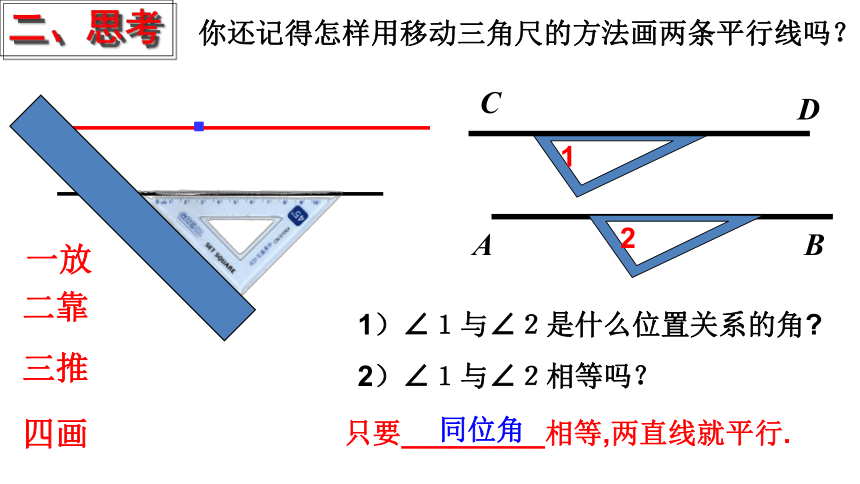
你还记得怎样用移动三角尺的方法画两条平行线吗?
一放
二靠
三推
四画
·
二、思考
1
2
A
B
C
D
1)∠1与∠2是什么位置关系的角?
2)∠1与∠2相等吗?
只要_________相等,两直线就平行.
同位角
1
2
a
A
B
C
D
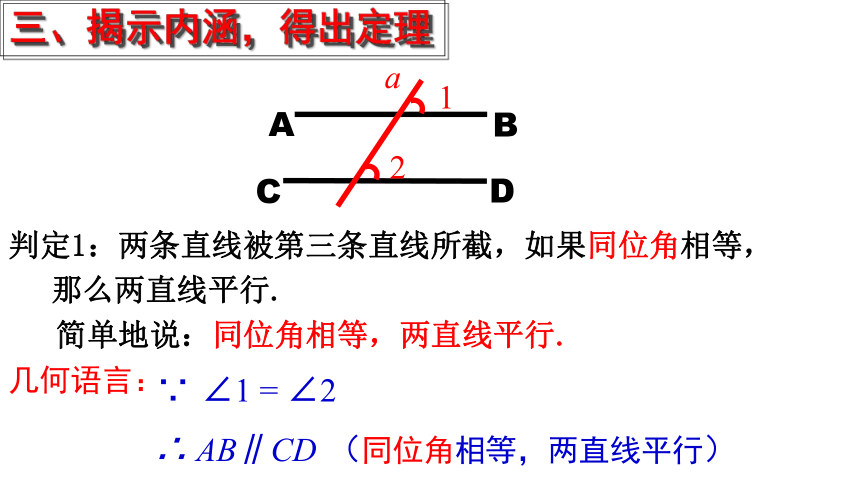
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
三、揭示内涵,得出定理
判定1:两条直线被第三条直线所截,如果同位角相等, 那么两直线平行.
简单地说:同位角相等,两直线平行.
小试牛刀
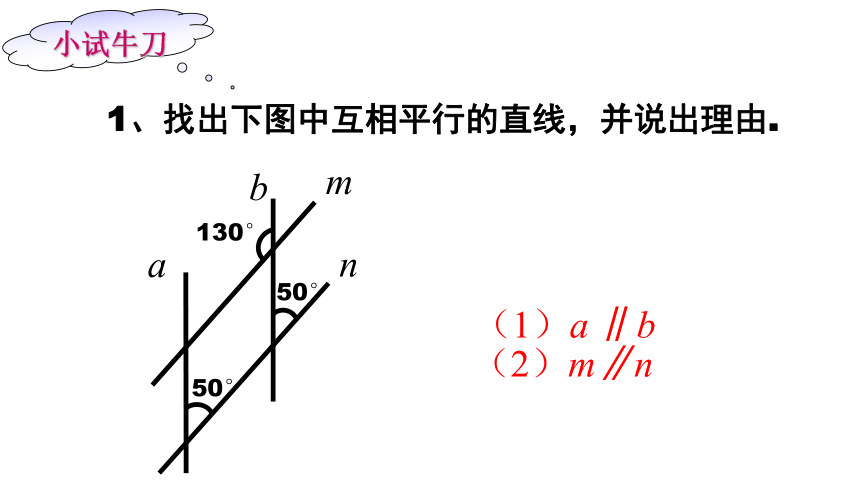
1、找出下图中互相平行的直线,并说出理由.
m
n
a
130°
50°
50°
(1)a ∥b
(2)m∥n
b
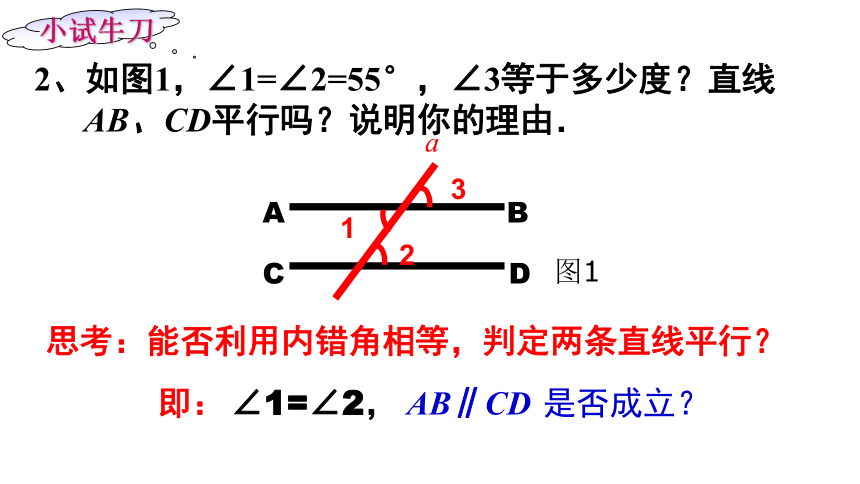
2、如图1,∠1=∠2=55°,∠3等于多少度?直线
AB、CD平行吗?说明你的理由.
小试牛刀
1
2
A
B
C
D
a
3
图1
思考:能否利用内错角相等,判定两条直线平行?
即: ∠1=∠2, AB∥CD 是否成立?
1
2
A
B
C
D
a
四、推理验证,得出定理
几何语言:
∴ AB∥CD (内错角相等,两直线平行)
∵ ∠1 = ∠2
判定2:两条直线被第三条直线所截,如果内错角相等, 那么两直线平行.
简单地说:内错角相等,两直线平行.
小试牛刀
3、如图2,∠1=55°,∠2=125°,∠3等于多少度?
直线AB、CD平行吗?说明你的理由.
2
1
A
B
C
D
a
3
图2
思考:能否利用同旁内角,判定两条直线平行?
即: ∠1+∠2=180°, AB∥CD 是否成立?
四、推理验证,得出定理
几何语言:
∴ AB∥CD (同旁内角互补,两直线平行)
∵ ∠1 + ∠2=180°
判定3:两条直线被第三条直线所截,如果同旁内角互补,
那么两直线平行.
简单地说:同旁内角互补,两直线平行.
2
1
A
B
C
D
a
3
四、新知链接
例1:如图,BE是AB的延长线.
(1)由∠CBE=∠A可以判断哪两条直线平行?根据是什么?
(2)由∠A+∠D=180°,可以判断哪两条直线平行?根据是什么?
.
P14 T1
例2:如图,在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行吗?为什么?
即:
如图,已知b?a,c?a,那么b//c吗?
符号语言:∵ b?a,c?a, ∴ b//c.
结论:
垂直于同一条直线的两条直线互相平行
怎样判断两条直线平行?
1. 在同一平面内,不相交的两条直线叫做平行线;
2. 如果两条直线 都和第三条直线平行,
那么这两条直线也互相平行;
3. 同位角相等,两直线平行;
4. 内错角相等,两直线平行;
5. 同旁内角互补,两直线平行;
6.在同一平面内,垂直于同一条直线的两条直线互相平行.
五、归纳小结
六、巩固练习
课本P15 T1
课本P15 T2
六、巩固练习
课本P16 T7
7、如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,由______________,得___ // ___
(2)如果∠D=∠DCG,由______________,得___ // ___
(3)如果∠D+∠DFE=180°,由__________________,
得___ // ___
如图:若∠AOD= ∠A+ ∠D,试判断AC与BD是否平行?
为什么?
A
B
C
D
O
七、能力提高
八、作业布置
1、课本P17 T11、T12
2、基础训练
学习目标:
1、运用平行线的画法对平行线的判定方法1进行推导;
2、分析并推导平行线的判定方法2、3、4,并对平行线判定的6种方法进行概括总结;
3、会正确运用平行线的判定方法对两条直线的位置关系进行判定即平行线判定的简单运用;
一、知识回顾
1、两条直线的位置关系有哪几种?
3、怎样判定两条直线平行?
2、平行线的公理是什么?
相交和平行
1)平行的定义:在同一平面内,不相交的两条直线互相平行;
2)推论:如果两条直线都和第三条直线平行,那么这两
条直线也互相平行(传递性);
问题:有没有其他的判定两直线互相平行的方法?
你还记得怎样用移动三角尺的方法画两条平行线吗?
一放
二靠
三推
四画
·
二、思考
1
2
A
B
C
D
1)∠1与∠2是什么位置关系的角?
2)∠1与∠2相等吗?
只要_________相等,两直线就平行.
同位角
1
2
a
A
B
C
D
几何语言:
∴ AB∥CD (同位角相等,两直线平行)
∵ ∠1 = ∠2
三、揭示内涵,得出定理
判定1:两条直线被第三条直线所截,如果同位角相等, 那么两直线平行.
简单地说:同位角相等,两直线平行.
小试牛刀
1、找出下图中互相平行的直线,并说出理由.
m
n
a
130°
50°
50°
(1)a ∥b
(2)m∥n
b
2、如图1,∠1=∠2=55°,∠3等于多少度?直线
AB、CD平行吗?说明你的理由.
小试牛刀
1
2
A
B
C
D
a
3
图1
思考:能否利用内错角相等,判定两条直线平行?
即: ∠1=∠2, AB∥CD 是否成立?
1
2
A
B
C
D
a
四、推理验证,得出定理
几何语言:
∴ AB∥CD (内错角相等,两直线平行)
∵ ∠1 = ∠2
判定2:两条直线被第三条直线所截,如果内错角相等, 那么两直线平行.
简单地说:内错角相等,两直线平行.
小试牛刀
3、如图2,∠1=55°,∠2=125°,∠3等于多少度?
直线AB、CD平行吗?说明你的理由.
2
1
A
B
C
D
a
3
图2
思考:能否利用同旁内角,判定两条直线平行?
即: ∠1+∠2=180°, AB∥CD 是否成立?
四、推理验证,得出定理
几何语言:
∴ AB∥CD (同旁内角互补,两直线平行)
∵ ∠1 + ∠2=180°
判定3:两条直线被第三条直线所截,如果同旁内角互补,
那么两直线平行.
简单地说:同旁内角互补,两直线平行.
2
1
A
B
C
D
a
3
四、新知链接
例1:如图,BE是AB的延长线.
(1)由∠CBE=∠A可以判断哪两条直线平行?根据是什么?
(2)由∠A+∠D=180°,可以判断哪两条直线平行?根据是什么?
.
P14 T1
例2:如图,在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行吗?为什么?
即:
如图,已知b?a,c?a,那么b//c吗?
符号语言:∵ b?a,c?a, ∴ b//c.
结论:
垂直于同一条直线的两条直线互相平行
怎样判断两条直线平行?
1. 在同一平面内,不相交的两条直线叫做平行线;
2. 如果两条直线 都和第三条直线平行,
那么这两条直线也互相平行;
3. 同位角相等,两直线平行;
4. 内错角相等,两直线平行;
5. 同旁内角互补,两直线平行;
6.在同一平面内,垂直于同一条直线的两条直线互相平行.
五、归纳小结
六、巩固练习
课本P15 T1
课本P15 T2
六、巩固练习
课本P16 T7
7、如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,由______________,得___ // ___
(2)如果∠D=∠DCG,由______________,得___ // ___
(3)如果∠D+∠DFE=180°,由__________________,
得___ // ___
如图:若∠AOD= ∠A+ ∠D,试判断AC与BD是否平行?
为什么?
A
B
C
D
O
七、能力提高
八、作业布置
1、课本P17 T11、T12
2、基础训练
