人教版七年级下册数学6.3实数(2无理数、实数概念)课件 (1)(共20张ppt)
文档属性
| 名称 | 人教版七年级下册数学6.3实数(2无理数、实数概念)课件 (1)(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览







文档简介
6.3 实数
义务教育课程标准实验教科书(人教版)
大家知道“万物皆数”这个观点吗?他是古希腊大数学家毕达哥拉斯提出的。他认为宇宙间的一切量都可以用整数或整数比(分数)表示,除此之外,就不再有别的什么东西了.
有一天,这一学派的西帕索斯发现边长为1的正方形的对角线的长度( )是个怪东西,既不能用整数表示又不能用整数的比表示,
他去找毕达哥拉斯,毕达哥拉斯也无法解释,又不敢承认它是一种新的数,因此下令封锁消息,西帕索斯为了坚持真理被迫流亡最后被害,这个怪东西“ ”从此后不知该何去何从,开启了“路漫漫其修远兮,吾将上下而求索” 的旅程…
这节课让我们跟随 “ ”的足迹来学习“实数” .
毕达哥拉斯
新课导入
学习目标
1. 了解无理数和实数的概念, 能对实数按要求分类;
2. 知道实数与数轴上的点具有 一一对应关系。
实数
总结:事实上,任何一个有理数都可以写成______或__________的形式.反过来,任何_______ 或 ___________也都是有理数.
2.把下列有理数写成小数的形式(整数写成小数点后
是0的形式,如3=3.0)
5 = 5.0
= 0.4
2
5
27
8
= 3.375
.
11
6
= 0.54
.
= 0.14
13
90
.
= 0.8
8
9
.
无限循环小数
5,
,
2
5
,
27
8
,
11
6
,
13
9
.
8
9
有限小数
无限循环小数
有理数部落(自主学习1)
1. 有理数包括____和____。
拒绝函
有限小数
有限小数
无限循环小数
整数
分数
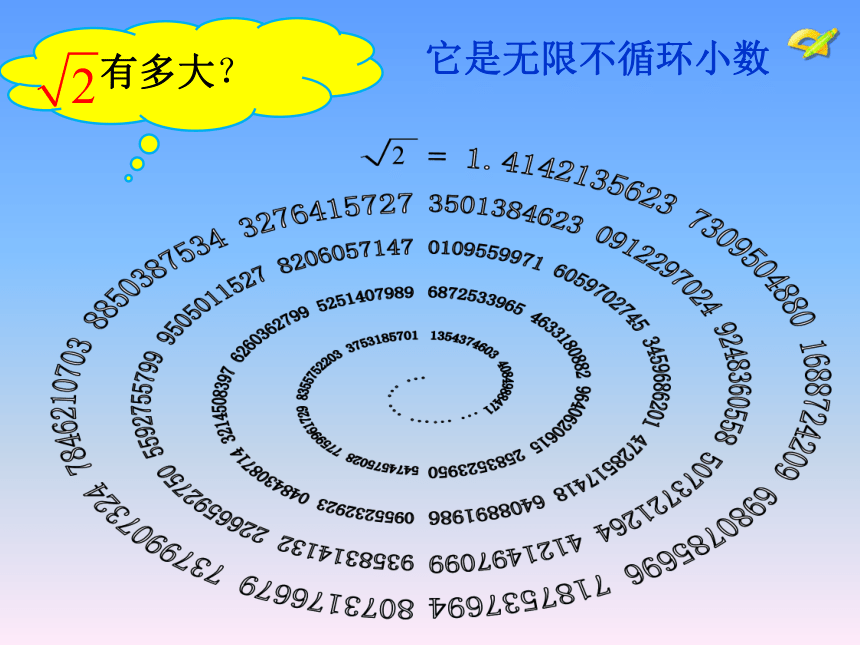
有多大?
它是无限不循环小数
有理数部落
无理数部落(自主学习2)
叫做无理数.
=1.70997594667669698935310…
π=3.1415926535897932384626…
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数
找朋友
无理数的定义:
1. 圆周率 π 及一些含有 π 的数
2.开方开不尽的数
3. 有一定的规律,但不循环的无限小数.
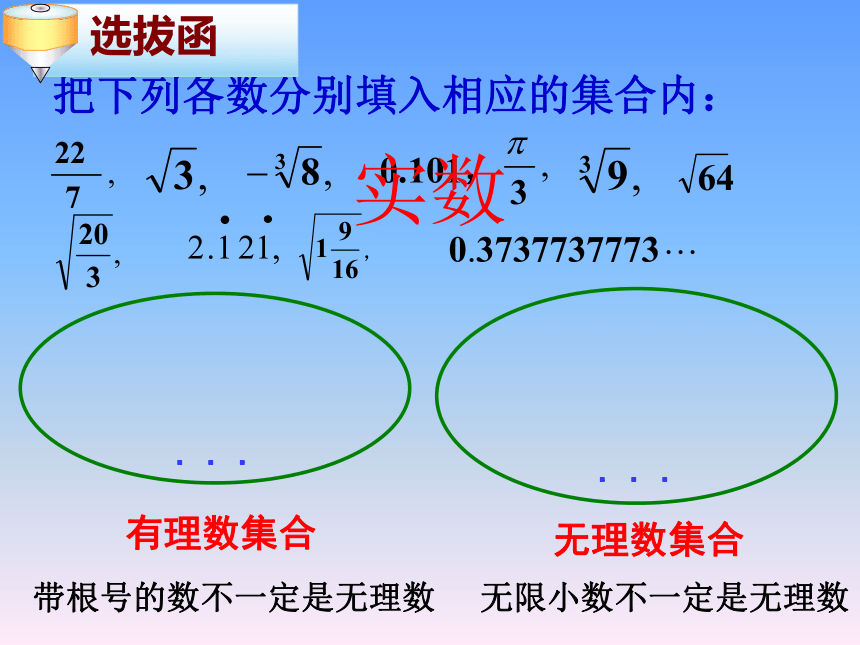
把下列各数分别填入相应的集合内:
0.101,
,
有理数集合
无理数集合
...
...
选拔函
带根号的数不一定是无理数
无限小数不一定是无理数
实数
思考:实数如何分类?
实数联盟
有理数和无理数统称实数
实数的定义:
有理数
无理数
(一)按定义分类
分数
整数
实数
实数的分类
无限不循环小数
有限小数或无限
循环小数
(二)按性质符号分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
实数的分类
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
有理数和无理数统称实数.
实数的分类
又遇麻烦(合作探究)
-4
-2
0
1
2
3
4
-1
-3
你能在数轴上找到表示Π的点吗?
有理数都可以用数轴上的点表示,无理数可以吗?
Π
无理数 可以用数轴上的点来表示。
π
又遇麻烦(合作探究)
-2
-1
1
2
B
A
C
1
1
O
你能在数轴上找到表示 ± 的点吗?
± 可以用数轴上的点来表示。
-2
-1
0
1
2
(数?点)
(点?数)
A
{ 实数 }: 数 a
实数a
点 A
一一对应
实数与数轴上的点一一对应
每一个实数(有理数、无理数)都可以用数轴上的一个点来表示.
反过来 ,数轴上的每一个点都表示一个实数.
·
·
如图所示,数轴上点A所表示的数为 ,点B到点A的距离为1个单位长度,则点B所表示的数是( )
和好如初(能力提升)
-2
-1
1
2
O
·
A
A B C 或 D 或
C
1.判断下列说法是否正确
(1)无限小数都是无理数。( )
(2)无理数都是无限小数。( )
(3)带根号的数都是无理数。( )
(4)无理数都是带根号的数。( )
(5)实数不是无理数就是有理数。( )
(6)所有的有理数都可以用数轴上的点表示,反过来数轴上的所有点都表示有理数。( )
(7)所有的实数都可以用数轴上的点表示,反过来数轴上的所有点都表示实数。( )
感谢函(达标测评)
√
×
×
×
√
×
√
整数有
有理数有
无理数有
实数有
课堂检测
2、填空
0.7272272227……
3.14159265,
3.14159265,
0.7272272227……
3.14159265,
0.7272272227……
(1).实数的概念
有理数和无理数统称为实数.
(2).实数的分类
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
4.实数与数轴上的点是一一对应的.
回顾历程(课堂小结)
1.来到“有理数”部落
2.找到朋友建立“无理数”部落→
3.与有理数合建“实数”联盟
→
无限不循环的小数叫做无理数.
祝同学们学习进步!
谢谢!
义务教育课程标准实验教科书(人教版)
大家知道“万物皆数”这个观点吗?他是古希腊大数学家毕达哥拉斯提出的。他认为宇宙间的一切量都可以用整数或整数比(分数)表示,除此之外,就不再有别的什么东西了.
有一天,这一学派的西帕索斯发现边长为1的正方形的对角线的长度( )是个怪东西,既不能用整数表示又不能用整数的比表示,
他去找毕达哥拉斯,毕达哥拉斯也无法解释,又不敢承认它是一种新的数,因此下令封锁消息,西帕索斯为了坚持真理被迫流亡最后被害,这个怪东西“ ”从此后不知该何去何从,开启了“路漫漫其修远兮,吾将上下而求索” 的旅程…
这节课让我们跟随 “ ”的足迹来学习“实数” .
毕达哥拉斯
新课导入
学习目标
1. 了解无理数和实数的概念, 能对实数按要求分类;
2. 知道实数与数轴上的点具有 一一对应关系。
实数
总结:事实上,任何一个有理数都可以写成______或__________的形式.反过来,任何_______ 或 ___________也都是有理数.
2.把下列有理数写成小数的形式(整数写成小数点后
是0的形式,如3=3.0)
5 = 5.0
= 0.4
2
5
27
8
= 3.375
.
11
6
= 0.54
.
= 0.14
13
90
.
= 0.8
8
9
.
无限循环小数
5,
,
2
5
,
27
8
,
11
6
,
13
9
.
8
9
有限小数
无限循环小数
有理数部落(自主学习1)
1. 有理数包括____和____。
拒绝函
有限小数
有限小数
无限循环小数
整数
分数
有多大?
它是无限不循环小数
有理数部落
无理数部落(自主学习2)
叫做无理数.
=1.70997594667669698935310…
π=3.1415926535897932384626…
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数
找朋友
无理数的定义:
1. 圆周率 π 及一些含有 π 的数
2.开方开不尽的数
3. 有一定的规律,但不循环的无限小数.
把下列各数分别填入相应的集合内:
0.101,
,
有理数集合
无理数集合
...
...
选拔函
带根号的数不一定是无理数
无限小数不一定是无理数
实数
思考:实数如何分类?
实数联盟
有理数和无理数统称实数
实数的定义:
有理数
无理数
(一)按定义分类
分数
整数
实数
实数的分类
无限不循环小数
有限小数或无限
循环小数
(二)按性质符号分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
实数的分类
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
有理数和无理数统称实数.
实数的分类
又遇麻烦(合作探究)
-4
-2
0
1
2
3
4
-1
-3
你能在数轴上找到表示Π的点吗?
有理数都可以用数轴上的点表示,无理数可以吗?
Π
无理数 可以用数轴上的点来表示。
π
又遇麻烦(合作探究)
-2
-1
1
2
B
A
C
1
1
O
你能在数轴上找到表示 ± 的点吗?
± 可以用数轴上的点来表示。
-2
-1
0
1
2
(数?点)
(点?数)
A
{ 实数 }: 数 a
实数a
点 A
一一对应
实数与数轴上的点一一对应
每一个实数(有理数、无理数)都可以用数轴上的一个点来表示.
反过来 ,数轴上的每一个点都表示一个实数.
·
·
如图所示,数轴上点A所表示的数为 ,点B到点A的距离为1个单位长度,则点B所表示的数是( )
和好如初(能力提升)
-2
-1
1
2
O
·
A
A B C 或 D 或
C
1.判断下列说法是否正确
(1)无限小数都是无理数。( )
(2)无理数都是无限小数。( )
(3)带根号的数都是无理数。( )
(4)无理数都是带根号的数。( )
(5)实数不是无理数就是有理数。( )
(6)所有的有理数都可以用数轴上的点表示,反过来数轴上的所有点都表示有理数。( )
(7)所有的实数都可以用数轴上的点表示,反过来数轴上的所有点都表示实数。( )
感谢函(达标测评)
√
×
×
×
√
×
√
整数有
有理数有
无理数有
实数有
课堂检测
2、填空
0.7272272227……
3.14159265,
3.14159265,
0.7272272227……
3.14159265,
0.7272272227……
(1).实数的概念
有理数和无理数统称为实数.
(2).实数的分类
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
4.实数与数轴上的点是一一对应的.
回顾历程(课堂小结)
1.来到“有理数”部落
2.找到朋友建立“无理数”部落→
3.与有理数合建“实数”联盟
→
无限不循环的小数叫做无理数.
祝同学们学习进步!
谢谢!
