人教版七年级下数学7.1.2平面直角坐标系(平面直角坐标系相关概念) (2)(共16张)
文档属性
| 名称 | 人教版七年级下数学7.1.2平面直角坐标系(平面直角坐标系相关概念) (2)(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 136.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 12:46:48 | ||
图片预览



文档简介
人教版七年级数学下
7.1 平面直角坐标系
第七章 平面直角坐标系
7.1.2 平面直角坐标系
复习引入
【问题1】请大家画出一条数轴.你能说出数轴的三要素吗?
【问题2】如图,数轴上的点A、B表示的数是什么?表示数字4的点是哪个点?
0
1
2
3
4
-3
-2
-1
A
B
C
A表示的数为-3 B表示的数为2
点C
数轴上每个点都对应一个实数,这个实数叫这个点在数轴上的坐标。例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。
0
1
2
3
4
-3
-2
-1
复习引入
【问题3】已知数轴上点C的坐标是4,点D的坐标是-2,你能在数轴上画出点C和点D吗?
知道数轴上一个点的坐标,这个的点在数轴
上的位置也就确定了。
【问题4】我们利用数轴可以确定直线上点的位置,能不能找到一种办法来确定平面内点的位置呢?
0
1
2
3
4
-3
-2
-1
D
C
A
B
C
D
思考:
类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内点的位置呢?
探索新知
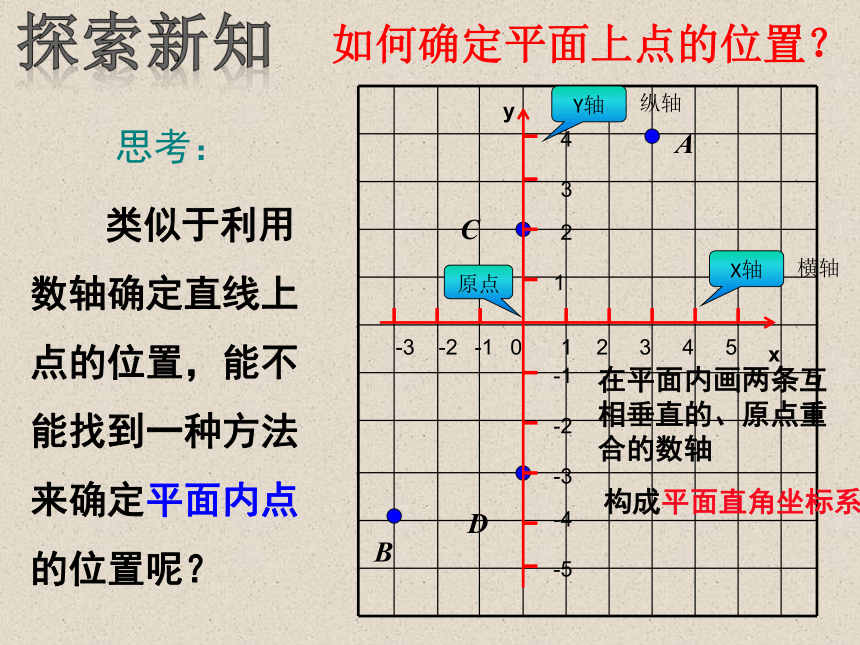
如何确定平面上点的位置?
1
2
3
4
5
0
-1
-2
-3
-1
-2
-3
-4
-5
1
2
3
4
x
X轴
横轴
y
Y轴
纵轴
原点
在平面内画两条互相垂直的、原点重合的数轴
构成平面直角坐标系.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
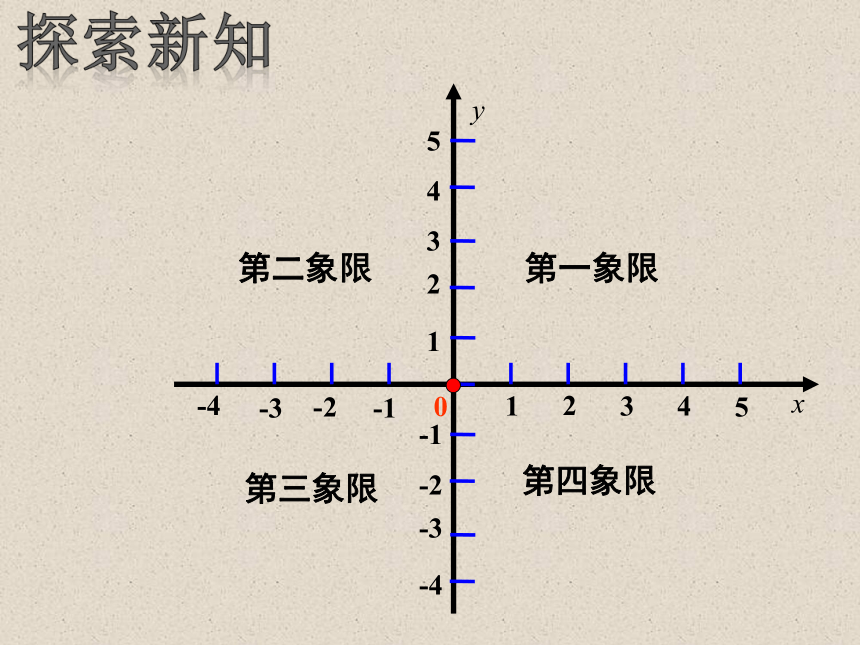
第一象限
第二象限
第三象限
第四象限
探索新知
A
B
C
D
x
y
1
2
3
4
5
-1
-2
-3
-1
-2
-3
1
2
3
4
-4
0
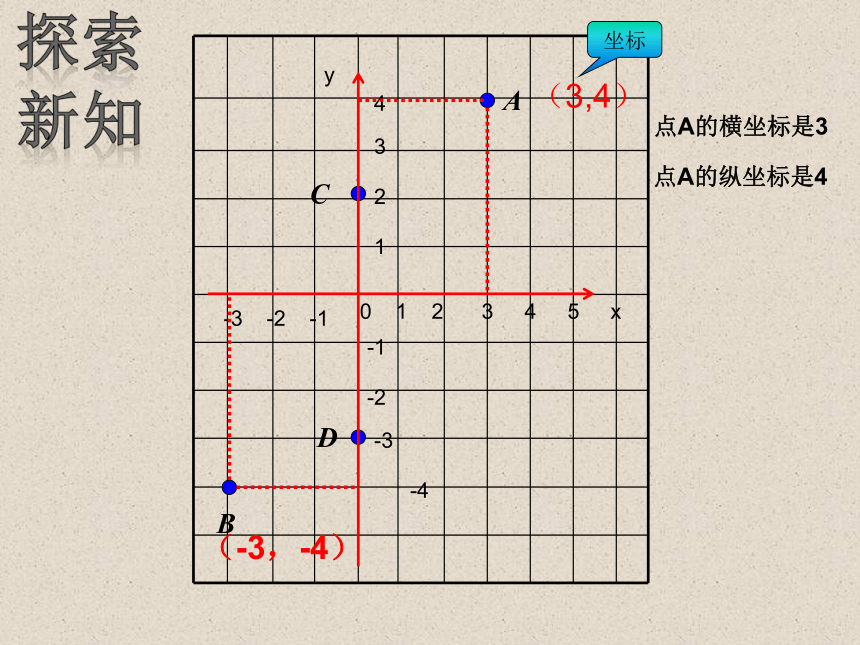
点A的横坐标是3
点A的纵坐标是4
(3,4)
坐标
(-3,-4)
探索
新知
探索新知
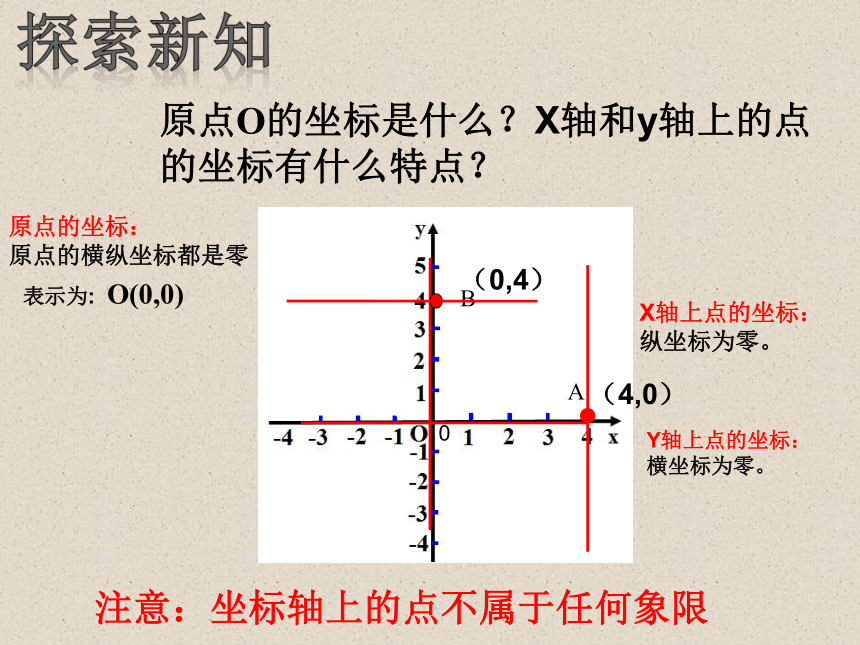
原点O的坐标是什么?X轴和y轴上的点
的坐标有什么特点?
原点的坐标:
原点的横纵坐标都是零
A
X轴上点的坐标:
纵坐标为零。
B
Y轴上点的坐标:
横坐标为零。
0
表示为: O(0,0)
(4,0)
(0,4)
注意:坐标轴上的点不属于任何象限
A
B
C
D
x
y
1
2
3
4
5
-1
-2
-3
-1
-2
-3
1
2
3
4
-4
0
A(3,4)
B(-3,-4)
C(0,2)
D(0,-3)
例1.指出图中点A、B、C、D的坐标.
发现规律
A(4,5)
B(-1,3)
C(-3,-3)
D(5,-4)
x
y
1
2
3
4
5
0
5
4
3
2
1
-2
-1
-3
-4
-5
-4
-3
-2
-1
-5
A
B
C
D
发现规律
例2.在平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2,-2),E(0,-4)
0
1
2
3
4
5
6
x
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
y
A
B
D
C
E
发现规律
对于坐标平面内任意一点M,都有唯一的一对
有序实数(x,y)(即点M的坐标)和它对应;反
过来,对于任意一对有序实数(x,y),在坐标平
面内都有唯一的一点M(即坐标为(x,y)的点)
和它对应,也就是说,坐标平面内的点与有序实数
对是一一对应的。
探索新知
象限内的点的坐标有什么特征?
A
第一象限:
横纵坐标全为正值
(+,+)
B
第二象限:
横坐标为负
纵坐标为正
(-,+)
C
第三象限:
横纵坐标全为负值
(-,-)
D
第四象限:
横坐标为正
纵坐标为负
(+,-)
根据下列各点的横纵坐标,指出
它们所在的象限:
A(-4,3)
发现规律
B(3,-4)
C(3,5)
D(-5,-3)
第二象限
第四象限
第一象限
第三象限
如图所示,正方形ABCD的边长是6,
如果以点A为原点,AB所在的直线为x轴,建立平面直角坐
标系,那么y轴是哪条直线?写出正方形顶点A, B, C, D
的坐标。
探索新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
x
y
A
(O)
B
C
D
A(0,0)
B(6,0)
C(6,6)
D(0,6)
探索新知
如图所示,正方形ABCD的边长是6,
如果以点A为原点,AB所在的直线为x轴,建立平面直角坐
标系,那么y轴是哪条直线?写出正方形顶点A, B, C, D
的坐标。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
x
y
A
O
B
C
D
请另建一个
平面直角坐标系
这时正方形的顶
点A, B, C, D,的
坐标又分别是多
少?
A(-2, 0)
B(4, 0)
C(4, 6)
D(-2, 6)
课堂小结
1. 平面直角坐标系及相关概念.
2.在平面直角坐标系中,根据坐标找出点,由点求出坐标.
3.象限内的点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.建立适当的平面直角坐标系描述点的坐标.
7.1 平面直角坐标系
第七章 平面直角坐标系
7.1.2 平面直角坐标系
复习引入
【问题1】请大家画出一条数轴.你能说出数轴的三要素吗?
【问题2】如图,数轴上的点A、B表示的数是什么?表示数字4的点是哪个点?
0
1
2
3
4
-3
-2
-1
A
B
C
A表示的数为-3 B表示的数为2
点C
数轴上每个点都对应一个实数,这个实数叫这个点在数轴上的坐标。例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。
0
1
2
3
4
-3
-2
-1
复习引入
【问题3】已知数轴上点C的坐标是4,点D的坐标是-2,你能在数轴上画出点C和点D吗?
知道数轴上一个点的坐标,这个的点在数轴
上的位置也就确定了。
【问题4】我们利用数轴可以确定直线上点的位置,能不能找到一种办法来确定平面内点的位置呢?
0
1
2
3
4
-3
-2
-1
D
C
A
B
C
D
思考:
类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内点的位置呢?
探索新知
如何确定平面上点的位置?
1
2
3
4
5
0
-1
-2
-3
-1
-2
-3
-4
-5
1
2
3
4
x
X轴
横轴
y
Y轴
纵轴
原点
在平面内画两条互相垂直的、原点重合的数轴
构成平面直角坐标系.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
第一象限
第二象限
第三象限
第四象限
探索新知
A
B
C
D
x
y
1
2
3
4
5
-1
-2
-3
-1
-2
-3
1
2
3
4
-4
0
点A的横坐标是3
点A的纵坐标是4
(3,4)
坐标
(-3,-4)
探索
新知
探索新知
原点O的坐标是什么?X轴和y轴上的点
的坐标有什么特点?
原点的坐标:
原点的横纵坐标都是零
A
X轴上点的坐标:
纵坐标为零。
B
Y轴上点的坐标:
横坐标为零。
0
表示为: O(0,0)
(4,0)
(0,4)
注意:坐标轴上的点不属于任何象限
A
B
C
D
x
y
1
2
3
4
5
-1
-2
-3
-1
-2
-3
1
2
3
4
-4
0
A(3,4)
B(-3,-4)
C(0,2)
D(0,-3)
例1.指出图中点A、B、C、D的坐标.
发现规律
A(4,5)
B(-1,3)
C(-3,-3)
D(5,-4)
x
y
1
2
3
4
5
0
5
4
3
2
1
-2
-1
-3
-4
-5
-4
-3
-2
-1
-5
A
B
C
D
发现规律
例2.在平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2,-2),E(0,-4)
0
1
2
3
4
5
6
x
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
1
2
3
4
5
y
A
B
D
C
E
发现规律
对于坐标平面内任意一点M,都有唯一的一对
有序实数(x,y)(即点M的坐标)和它对应;反
过来,对于任意一对有序实数(x,y),在坐标平
面内都有唯一的一点M(即坐标为(x,y)的点)
和它对应,也就是说,坐标平面内的点与有序实数
对是一一对应的。
探索新知
象限内的点的坐标有什么特征?
A
第一象限:
横纵坐标全为正值
(+,+)
B
第二象限:
横坐标为负
纵坐标为正
(-,+)
C
第三象限:
横纵坐标全为负值
(-,-)
D
第四象限:
横坐标为正
纵坐标为负
(+,-)
根据下列各点的横纵坐标,指出
它们所在的象限:
A(-4,3)
发现规律
B(3,-4)
C(3,5)
D(-5,-3)
第二象限
第四象限
第一象限
第三象限
如图所示,正方形ABCD的边长是6,
如果以点A为原点,AB所在的直线为x轴,建立平面直角坐
标系,那么y轴是哪条直线?写出正方形顶点A, B, C, D
的坐标。
探索新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
x
y
A
(O)
B
C
D
A(0,0)
B(6,0)
C(6,6)
D(0,6)
探索新知
如图所示,正方形ABCD的边长是6,
如果以点A为原点,AB所在的直线为x轴,建立平面直角坐
标系,那么y轴是哪条直线?写出正方形顶点A, B, C, D
的坐标。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
x
y
A
O
B
C
D
请另建一个
平面直角坐标系
这时正方形的顶
点A, B, C, D,的
坐标又分别是多
少?
A(-2, 0)
B(4, 0)
C(4, 6)
D(-2, 6)
课堂小结
1. 平面直角坐标系及相关概念.
2.在平面直角坐标系中,根据坐标找出点,由点求出坐标.
3.象限内的点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.建立适当的平面直角坐标系描述点的坐标.
