人教版数学 八年级上册 11.1.2 三角形的高-中线与角平分线(共22张)
文档属性
| 名称 | 人教版数学 八年级上册 11.1.2 三角形的高-中线与角平分线(共22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 598.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 13:10:54 | ||
图片预览


文档简介
11.1.2
三角形的高、
中线与角平分线
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
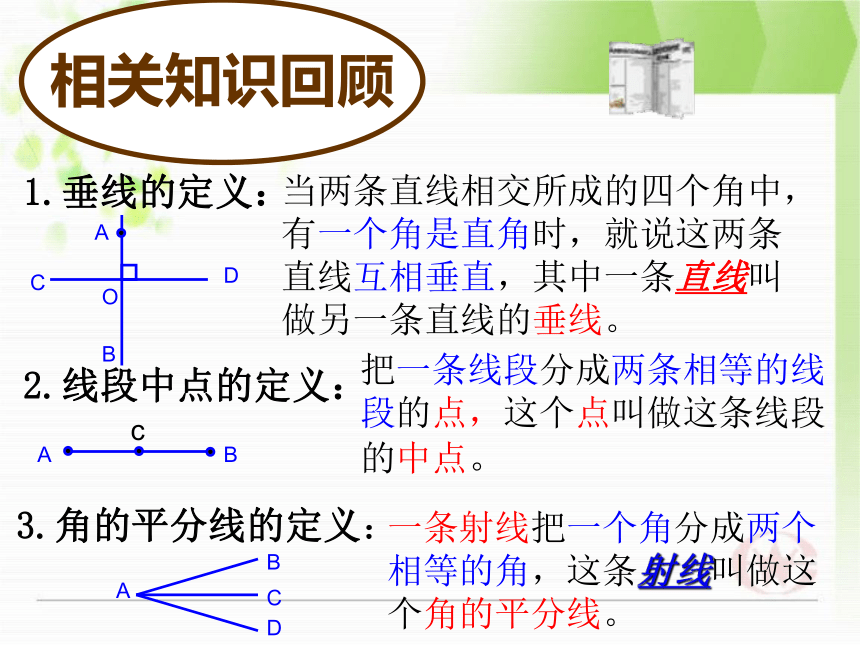
2.线段中点的定义:
3.角的平分线的定义:
1.垂线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
把一条线段分成两条相等的线段的点,这个点叫做这条线段的中点。
当两条直线相交所成的四个角中,
有一个角是直角时,就说这两条
直线互相垂直,其中一条直线叫
做另一条直线的垂线。
相关知识回顾
A
D
B
c
A
B
A
B
C
D
C
O
新知讲解
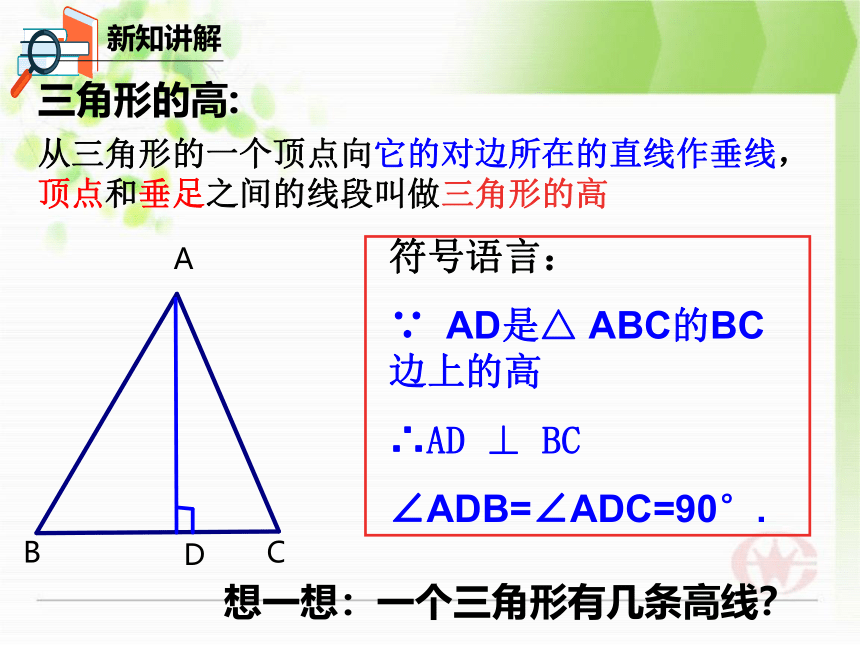
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高
符号语言:
∵
AD是△
ABC的BC边上的高
∴AD
⊥
BC
∠ADB=∠ADC=90°.
A
B
C
D
想一想:一个三角形有几条高线?
三角形的高:
新知讲解
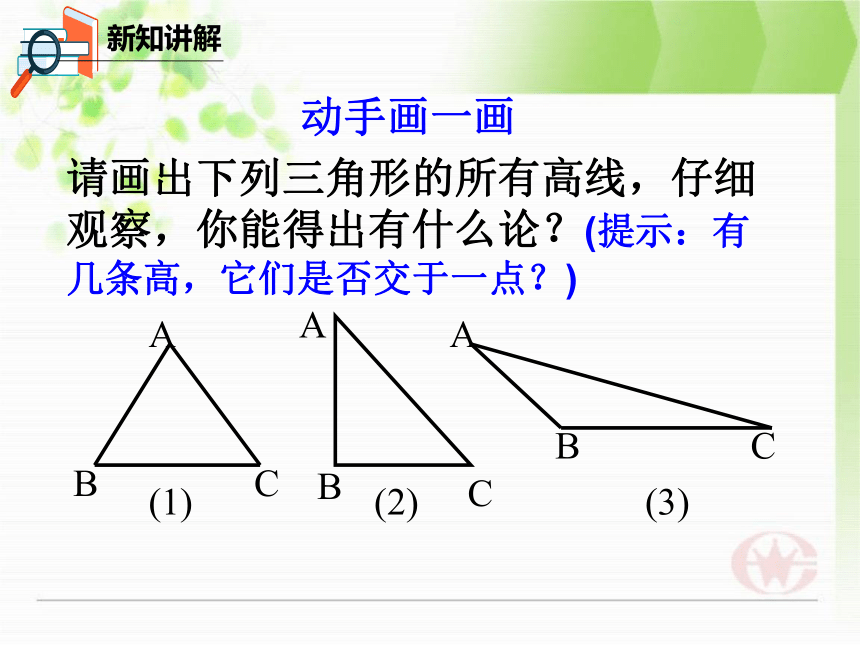
动手画一画
请画出下列三角形的所有高线,仔细观察,你能得出有什么论?(提示:有几条高,它们是否交于一点?)
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
O
A
B
D
E
F
A
B
C
(D)
●
A
B
C
D
F
E
O
(O)
●
●
C
E
(F)
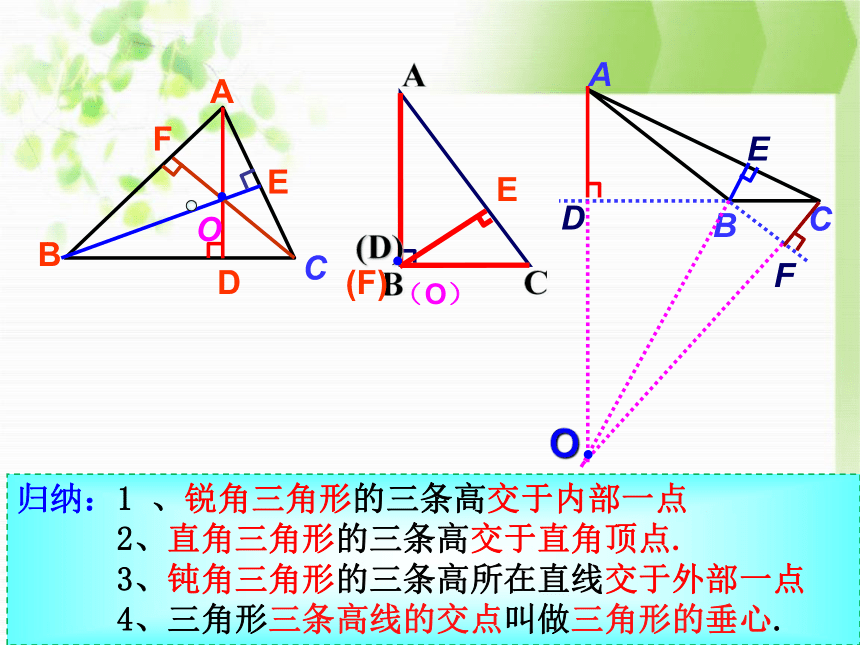
归纳:1
、锐角三角形的三条高交于内部一点
2、直角三角形的三条高交于直角顶点.
3、钝角三角形的三条高所在直线交于外部一点
4、三角形三条高线的交点叫做三角形的垂心.
新知讲解
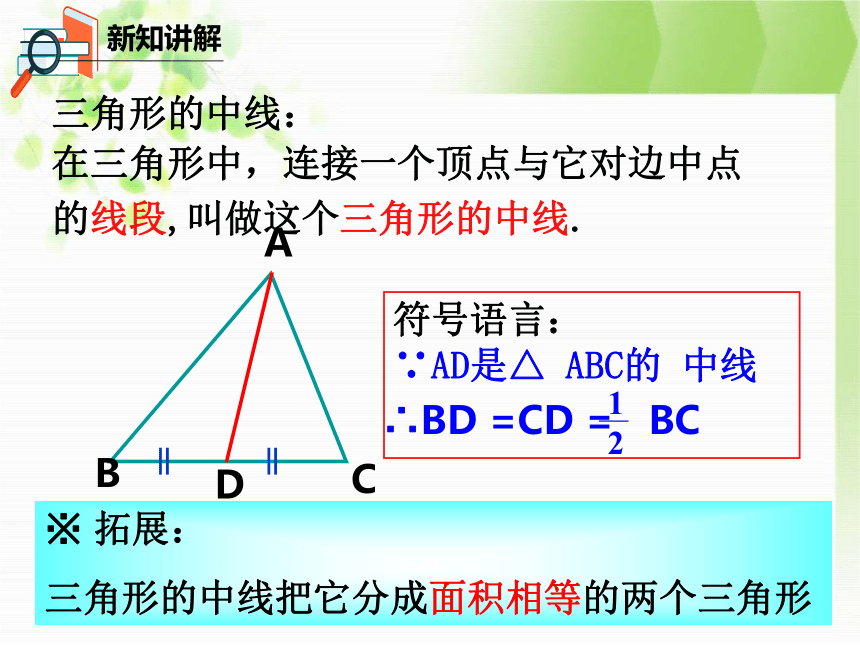
在三角形中,连接一个顶点与它对边中点
的线段,叫做这个三角形的中线.
A
B
C
D
符号语言:
∵AD是△
ABC的
中线
∴BD
=CD
=
BC
1
2
三角形的中线:
※
拓展:
三角形的中线把它分成面积相等的两个三角形
自主探究
归纳:
1
、任意三角形的三条中线都在三角形的内部,并且交于一点.
2、三角形三条中线的交点叫做三角形的重心.
请画出下列三角形的所有中线,仔细观察,
你能得出有什么论?
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
新知讲解
A
B
C
D
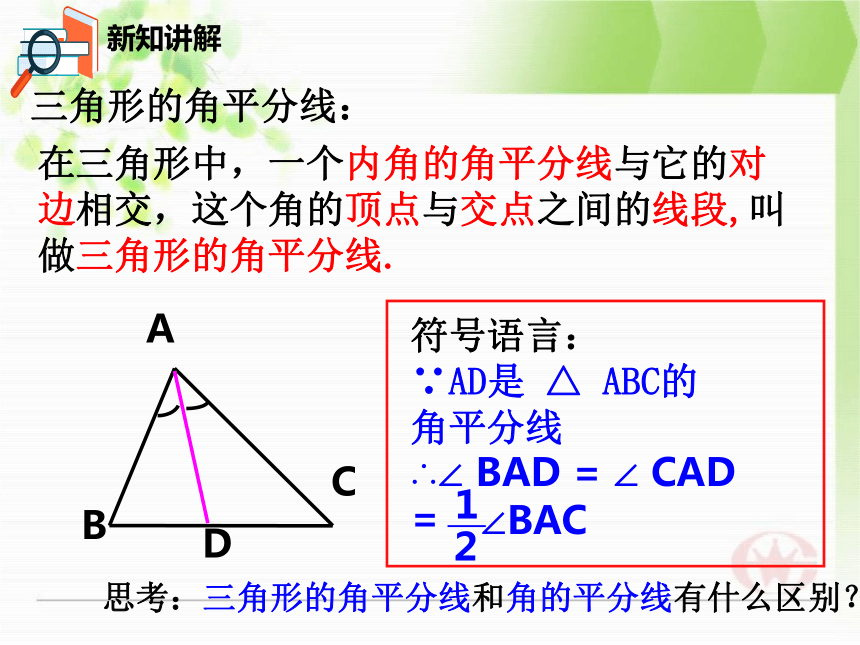
符号语言:
∵AD是
△
ABC的
角平分线
∴∠
BAD
=
∠
CAD
=
1
2
∠BAC
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
三角形的角平分线:
思考:三角形的角平分线和角的平分线有什么区别?
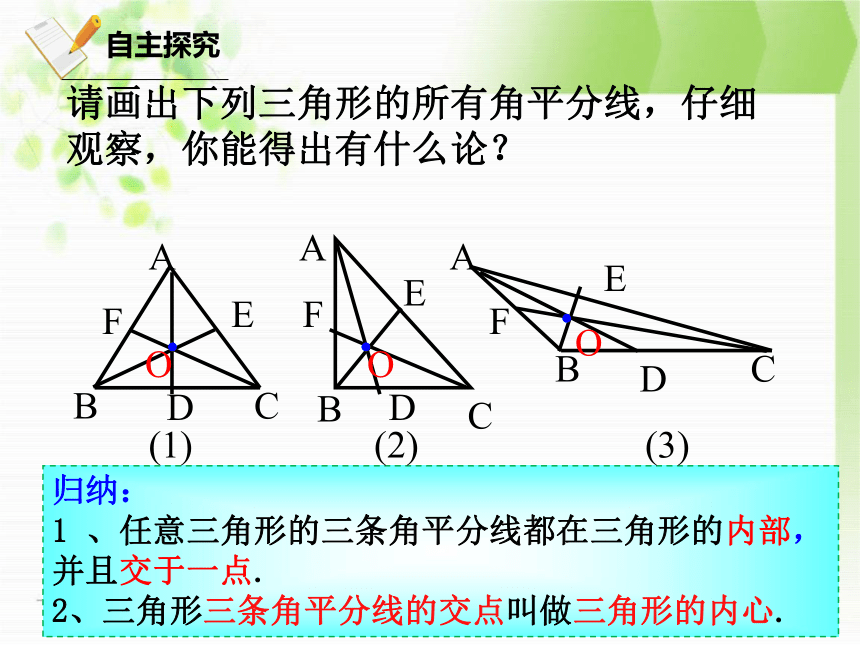
自主探究
请画出下列三角形的所有角平分线,仔细观察,你能得出有什么论?
归纳:
1
、任意三角形的三条角平分线都在三角形的内部,并且交于一点.
2、三角形三条角平分线的交点叫做三角形的内心.
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
O
A
B
D
E
F
A
B
C
(D)
●
A
B
C
D
F
E
O
(O)
●
●
C
E
(F)
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
课堂练习
1.如果三角形的三条高的交点恰好是三角形的
一个顶点,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
C
2.如图,D是BC的中点,E是AC的中点.
若S△ADE=2,则S△ADC=
.
4
随堂检测
3、下列各组图形中,哪一组图形中AD是△ABC
的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
4.如图所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是(
)
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.∠C的对边是DE
D
5.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=9
0°;
CE
BC
∠CAD
∠BAC
∠AFC
课堂小结
三角形的
重要线段
概念
图形
符号语言
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中点的线段
∵
AD是△ABC的中线.
∴
BD=CD=
?BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的角平分线
∴
∠1=∠2=
?
∠BAC
1、三角形三条高线的交点叫做三角形的垂心.
2、三角形三条中线的交点叫做三角形的重心.
3、三角形三条角平分线的交点叫做三角形的内心.
当堂练习
1.下列说法正确的是
( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是
( )
A.①②
B.③④
C.①④
D.②③
D
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有
( )
A.2条
B.3条
C.4条
D.5条
4.下列各组图形中,哪一组图形中AD是△ABC
的BC边上的高
(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2______.
图①
图②
AF
DC
∠2
2∠4
AC
∠ABC
6.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
7.如图,AE是
△ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵
∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE=
∠BAC.
8.如图,在△ABC中,AD是△ABC的高,AE是
△ABC的角平分线,已知∠BAC=82°,∠C=40°,
求∠DAE的大小.
解:
∵
AD是△ABC的高,
∴∠ADC=90°.
∵
∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-(∠ADC+∠C
)
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°=
9°.
B
A
C
D
E
课堂小结
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的高、
中线与角平分线
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
2.线段中点的定义:
3.角的平分线的定义:
1.垂线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
把一条线段分成两条相等的线段的点,这个点叫做这条线段的中点。
当两条直线相交所成的四个角中,
有一个角是直角时,就说这两条
直线互相垂直,其中一条直线叫
做另一条直线的垂线。
相关知识回顾
A
D
B
c
A
B
A
B
C
D
C
O
新知讲解
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高
符号语言:
∵
AD是△
ABC的BC边上的高
∴AD
⊥
BC
∠ADB=∠ADC=90°.
A
B
C
D
想一想:一个三角形有几条高线?
三角形的高:
新知讲解
动手画一画
请画出下列三角形的所有高线,仔细观察,你能得出有什么论?(提示:有几条高,它们是否交于一点?)
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
O
A
B
D
E
F
A
B
C
(D)
●
A
B
C
D
F
E
O
(O)
●
●
C
E
(F)
归纳:1
、锐角三角形的三条高交于内部一点
2、直角三角形的三条高交于直角顶点.
3、钝角三角形的三条高所在直线交于外部一点
4、三角形三条高线的交点叫做三角形的垂心.
新知讲解
在三角形中,连接一个顶点与它对边中点
的线段,叫做这个三角形的中线.
A
B
C
D
符号语言:
∵AD是△
ABC的
中线
∴BD
=CD
=
BC
1
2
三角形的中线:
※
拓展:
三角形的中线把它分成面积相等的两个三角形
自主探究
归纳:
1
、任意三角形的三条中线都在三角形的内部,并且交于一点.
2、三角形三条中线的交点叫做三角形的重心.
请画出下列三角形的所有中线,仔细观察,
你能得出有什么论?
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
新知讲解
A
B
C
D
符号语言:
∵AD是
△
ABC的
角平分线
∴∠
BAD
=
∠
CAD
=
1
2
∠BAC
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
三角形的角平分线:
思考:三角形的角平分线和角的平分线有什么区别?
自主探究
请画出下列三角形的所有角平分线,仔细观察,你能得出有什么论?
归纳:
1
、任意三角形的三条角平分线都在三角形的内部,并且交于一点.
2、三角形三条角平分线的交点叫做三角形的内心.
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
O
A
B
D
E
F
A
B
C
(D)
●
A
B
C
D
F
E
O
(O)
●
●
C
E
(F)
A
B
C
A
B
C
A
B
C
(1)
(2)
(3)
D
D
D
E
F
E
F
E
F
O
O
O
●
●
●
课堂练习
1.如果三角形的三条高的交点恰好是三角形的
一个顶点,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
C
2.如图,D是BC的中点,E是AC的中点.
若S△ADE=2,则S△ADC=
.
4
随堂检测
3、下列各组图形中,哪一组图形中AD是△ABC
的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
4.如图所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是(
)
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.∠C的对边是DE
D
5.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=9
0°;
CE
BC
∠CAD
∠BAC
∠AFC
课堂小结
三角形的
重要线段
概念
图形
符号语言
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中点的线段
∵
AD是△ABC的中线.
∴
BD=CD=
?BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的角平分线
∴
∠1=∠2=
?
∠BAC
1、三角形三条高线的交点叫做三角形的垂心.
2、三角形三条中线的交点叫做三角形的重心.
3、三角形三条角平分线的交点叫做三角形的内心.
当堂练习
1.下列说法正确的是
( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是
( )
A.①②
B.③④
C.①④
D.②③
D
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有
( )
A.2条
B.3条
C.4条
D.5条
4.下列各组图形中,哪一组图形中AD是△ABC
的BC边上的高
(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2______.
图①
图②
AF
DC
∠2
2∠4
AC
∠ABC
6.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
7.如图,AE是
△ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵
∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE=
∠BAC.
8.如图,在△ABC中,AD是△ABC的高,AE是
△ABC的角平分线,已知∠BAC=82°,∠C=40°,
求∠DAE的大小.
解:
∵
AD是△ABC的高,
∴∠ADC=90°.
∵
∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-(∠ADC+∠C
)
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°=
9°.
B
A
C
D
E
课堂小结
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
