人教版数学八年级上册第11章三角形复习课件(18张ppt)
文档属性
| 名称 | 人教版数学八年级上册第11章三角形复习课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 743.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览





文档简介
课前准备
请同学们准备好教材、练习本、学案、三角板、量角器及手机
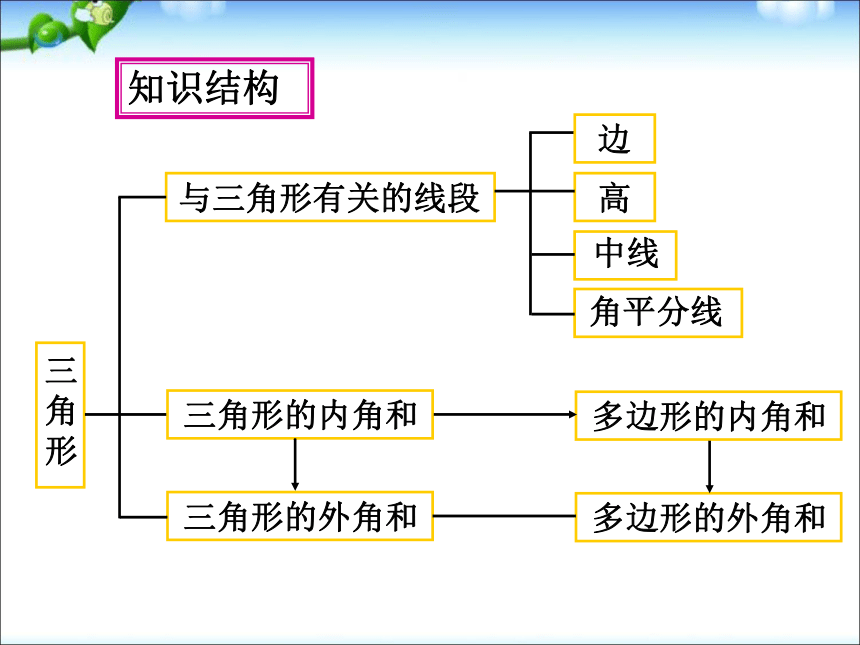
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
知识结构
人教版八年级上册
第十一章 三角形复习课
———复习题 11
解决问题
4、已知等腰三角形两边长分别是7和4,则此等腰三角形的周长为( )
变式:若等腰三角形两边长分别是8和4,则这个等腰三角形的周长为_________
A.18
B.15
C.18或15
D.无法确定
C
20
解决问题
7、一个正多边形的每一个内角都等于120 °,则这个正多边形的边数为_________
对应练习:一个多边形的每一个内角都等于135 °,则这个多边形的边数为_________
1
D
C
A
B
解决问题
9.已知∠B= 42 °,∠A+10°= ∠1, ∠ACD= 64° 试说明AB∥CD
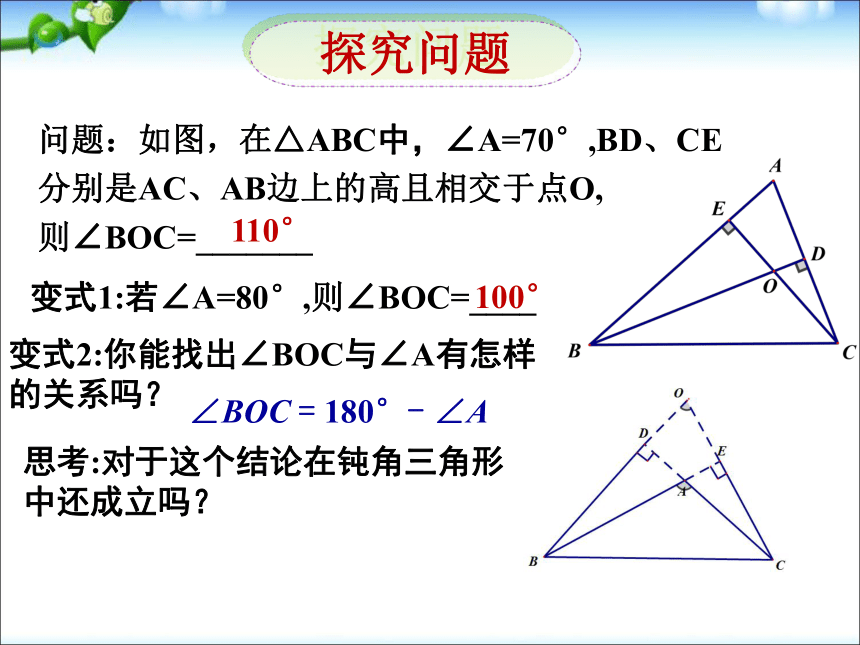
探究问题
问题:如图,在△ABC中,∠A=70°,BD、CE分别是AC、AB边上的高且相交于点O,
则∠BOC=_______
变式1:若∠A=80°,则∠BOC=____
变式2:你能找出∠BOC与∠A有怎样
的关系吗?
思考:对于这个结论在钝角三角形
中还成立吗?
110°
100°
∠BOC = 180°- ∠A
探究问题
问题:如图,在△ABC中,∠A=70°,BD、CE分别是AC、AB边上的高且相交于点O,
则∠BOC=_______
变式3:如图,在△ABC中,∠A=70°,BD、CE分别是△ABC的两条内角平分线且相交于点O,
则∠BOC=_______
若∠A=80呢?
∠BOC=_______
125°
130°
探究问题
变式4:如图,在△ABC中,∠A=90°,BD、CE分别是△ABC的两条内角平分线且相交于点O,
则∠BOC=_______
根据上述计算,你能猜想出∠BOC 与∠A 之间的数量关系吗?
∠BOC = 90°+ ∠A
135°
证明结论
已知:如图,在锐角△ABC中,BD、CE分别是△ABC的两条内角平分线且相交于点O,求证:∠BOC= 90° + ∠A
证明结论
已知:如图,在钝角△ABC中,BD、CE分别是△ABC的两条内角平分线且相交于点O,求证:∠BOC= 90° + ∠A
得出结论
如图,在△ABC中,若BD、CE分别是△ABC的两条内角平分线且相交于点O,
则可得结论:
结论运用
(1)已知:如图,在△ABC中,BD、CE分别是△ABC的两条内角平分线且相交于点O,
若∠A=50°,则∠BOC= _______
(2)如图,若∠AOB=140°, AD、BE分别是△ABC的两条内角平分线且相交于点O则∠C= _______
115 °
100°
拓展提升
变式5:如图,在△ABC中,BD、CE分别是△ABC的两条外角平分线且相交于点O,则∠BOC与∠A有怎样的关系?
结论:∠BOC = 90°- ∠A
拓展提升
变式6:如图,在△ABC中,BO、CO分别是△ABC的一条内角平分线与一条外角平分线,则∠BOC与∠A有怎样的关系?
结论:∠BOC = ∠A
请你说给大家听听
这节课你有哪些收获?
课堂小结
课堂小结
1、知识与技能:
(1)进一步熟练掌握与三角形有关的线段、角等
相关知识,学会如何运用这些知识解决问题
2、数学思想方法:
(1)分类讨论的数学思想
(2)从特殊到一般的数学思想
3、相关的结论
布置作业
B层:(1)教材28页1、3、4
(2)作业卷(基础部分)
A层:(1)教材29页9、10、11、12
(2)作业卷
请同学们准备好教材、练习本、学案、三角板、量角器及手机
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
知识结构
人教版八年级上册
第十一章 三角形复习课
———复习题 11
解决问题
4、已知等腰三角形两边长分别是7和4,则此等腰三角形的周长为( )
变式:若等腰三角形两边长分别是8和4,则这个等腰三角形的周长为_________
A.18
B.15
C.18或15
D.无法确定
C
20
解决问题
7、一个正多边形的每一个内角都等于120 °,则这个正多边形的边数为_________
对应练习:一个多边形的每一个内角都等于135 °,则这个多边形的边数为_________
1
D
C
A
B
解决问题
9.已知∠B= 42 °,∠A+10°= ∠1, ∠ACD= 64° 试说明AB∥CD
探究问题
问题:如图,在△ABC中,∠A=70°,BD、CE分别是AC、AB边上的高且相交于点O,
则∠BOC=_______
变式1:若∠A=80°,则∠BOC=____
变式2:你能找出∠BOC与∠A有怎样
的关系吗?
思考:对于这个结论在钝角三角形
中还成立吗?
110°
100°
∠BOC = 180°- ∠A
探究问题
问题:如图,在△ABC中,∠A=70°,BD、CE分别是AC、AB边上的高且相交于点O,
则∠BOC=_______
变式3:如图,在△ABC中,∠A=70°,BD、CE分别是△ABC的两条内角平分线且相交于点O,
则∠BOC=_______
若∠A=80呢?
∠BOC=_______
125°
130°
探究问题
变式4:如图,在△ABC中,∠A=90°,BD、CE分别是△ABC的两条内角平分线且相交于点O,
则∠BOC=_______
根据上述计算,你能猜想出∠BOC 与∠A 之间的数量关系吗?
∠BOC = 90°+ ∠A
135°
证明结论
已知:如图,在锐角△ABC中,BD、CE分别是△ABC的两条内角平分线且相交于点O,求证:∠BOC= 90° + ∠A
证明结论
已知:如图,在钝角△ABC中,BD、CE分别是△ABC的两条内角平分线且相交于点O,求证:∠BOC= 90° + ∠A
得出结论
如图,在△ABC中,若BD、CE分别是△ABC的两条内角平分线且相交于点O,
则可得结论:
结论运用
(1)已知:如图,在△ABC中,BD、CE分别是△ABC的两条内角平分线且相交于点O,
若∠A=50°,则∠BOC= _______
(2)如图,若∠AOB=140°, AD、BE分别是△ABC的两条内角平分线且相交于点O则∠C= _______
115 °
100°
拓展提升
变式5:如图,在△ABC中,BD、CE分别是△ABC的两条外角平分线且相交于点O,则∠BOC与∠A有怎样的关系?
结论:∠BOC = 90°- ∠A
拓展提升
变式6:如图,在△ABC中,BO、CO分别是△ABC的一条内角平分线与一条外角平分线,则∠BOC与∠A有怎样的关系?
结论:∠BOC = ∠A
请你说给大家听听
这节课你有哪些收获?
课堂小结
课堂小结
1、知识与技能:
(1)进一步熟练掌握与三角形有关的线段、角等
相关知识,学会如何运用这些知识解决问题
2、数学思想方法:
(1)分类讨论的数学思想
(2)从特殊到一般的数学思想
3、相关的结论
布置作业
B层:(1)教材28页1、3、4
(2)作业卷(基础部分)
A层:(1)教材29页9、10、11、12
(2)作业卷
