人教版数学八年级下册 课件:19.2.2一次函数的性质和图象(2)(共19张)
文档属性
| 名称 | 人教版数学八年级下册 课件:19.2.2一次函数的性质和图象(2)(共19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 122.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 12:52:04 | ||
图片预览





文档简介
19.2.2一次函数的性质和图象2
学习目标
1.通过课本93页“探究”,从解析式上看,一次函数y=kx+b(k≠0)与正比例函数y=kx只差一个常数b,学生说出一次函数y=kx+b(k≠0)中b对函数图像有什么影响?
2.能根据一次函数的图象和函数关系式,探索并理解一次函数的性质.
重点难点
重点难点:
1.函数图像的性质.
2.一次函数y=kx+b(k≠0)中k,b对函数图像的影响.
完成了解感知中的题目
时间:6分钟
要求:1、认真阅读课本86-87页内容
2、独立完成了解感知中的题目
3、不能完成的题用红笔圈起来
直线y=kx+b可能在坐标系中的
哪些位置?
思考
y=kx+b
x
y
o
x
y
o
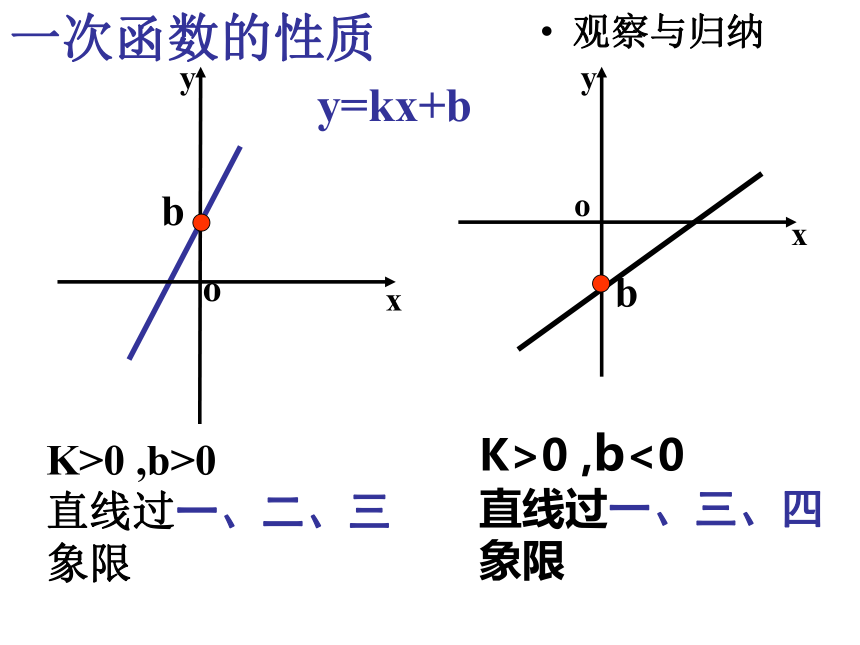
K>0 ,b<0
直线过一、三、四象限
一次函数的性质
观察与归纳
b
b
K>0 ,b>0
直线过一、二、三象限
y=kx+b
x
y
o
x
y
o
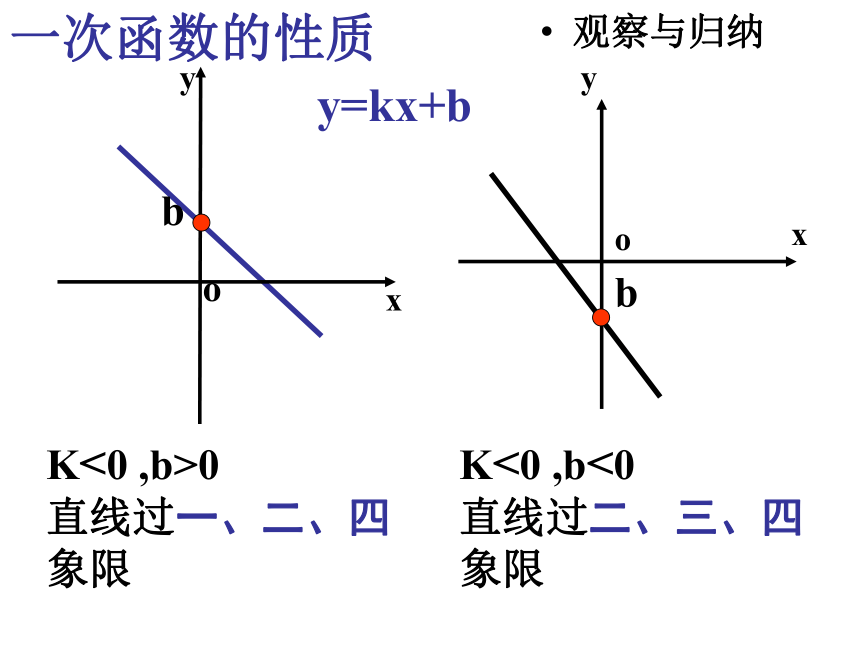
一次函数的性质
观察与归纳
b
b
K<0 ,b>0
直线过一、二、四象限
K<0 ,b<0
直线过二、三、四象限
直线y=kx
x
y
o
x
y
o
K>0 k<0
一、三象限 二、四象限
正比例函数的性质
观察与归纳
直线
经过坐标系中的象限
y=x+1
y=3x-1
y= -2x-1
y= 3-2x
一、二、三
二、三、四
一、三、四
一、二、四
完成深入学习中的题目。
时间:8分钟
要求:1、自主探究完成题目
2、不会的题目用笔画出来
1.画出函数y=-6x与y=-6x+5的图象.
二、探究新知
x
-2
-1
0
1
2
y=-6x
y=-6x+5
12
6
0
-6
-12
17
11
5
-1
-7
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
2.观察与比较.
这两个函数的图象形状都是 ,并且倾斜程度 .函数y=6x的图象经过原点,函数y=-6x+5的图象与y轴交于点 ,即它可以看作由直线y=-6x向 平移 个单位长度得到.
比较上面两个函数图象的相同点与不同点.填出你的观察结果并与同伴交流.
一条直线
(0,5)
相同
上
5
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
5.结论.
一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移︱b︱个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移)
完成迁移运用中的题目
时间:7分钟
要求:1、自主探究完成题目
2、不会的题目用笔画出来
3、注意解题步骤的规范性
图象特征
大致图象
K>0
b>0
b=0
b<0
上升,交点在y轴的正半轴。
上升,交点在原点。
上升,交点在y轴的负半轴。
x
y
0
x
y
0
x
y
0
知识归纳
图象特征
大致图象
K<0
b>0
b=0
b<0
下降,交点在y轴的正半轴。
下降,交点在原点。
下降,交点在y轴的负半轴。
x
y
0
x
y
0
x
y
0
知识归纳
课堂小结
这节课我们学到了什么?
完成当堂训练中的题目
时间:7分钟
要求:1、自主探究完成题目
2、不会的题目用笔画出来
3、注意解题步骤的规范性
让我们为激情小组
表示祝贺,
其他小组再接再厉,
永不言输!
学习目标
1.通过课本93页“探究”,从解析式上看,一次函数y=kx+b(k≠0)与正比例函数y=kx只差一个常数b,学生说出一次函数y=kx+b(k≠0)中b对函数图像有什么影响?
2.能根据一次函数的图象和函数关系式,探索并理解一次函数的性质.
重点难点
重点难点:
1.函数图像的性质.
2.一次函数y=kx+b(k≠0)中k,b对函数图像的影响.
完成了解感知中的题目
时间:6分钟
要求:1、认真阅读课本86-87页内容
2、独立完成了解感知中的题目
3、不能完成的题用红笔圈起来
直线y=kx+b可能在坐标系中的
哪些位置?
思考
y=kx+b
x
y
o
x
y
o
K>0 ,b<0
直线过一、三、四象限
一次函数的性质
观察与归纳
b
b
K>0 ,b>0
直线过一、二、三象限
y=kx+b
x
y
o
x
y
o
一次函数的性质
观察与归纳
b
b
K<0 ,b>0
直线过一、二、四象限
K<0 ,b<0
直线过二、三、四象限
直线y=kx
x
y
o
x
y
o
K>0 k<0
一、三象限 二、四象限
正比例函数的性质
观察与归纳
直线
经过坐标系中的象限
y=x+1
y=3x-1
y= -2x-1
y= 3-2x
一、二、三
二、三、四
一、三、四
一、二、四
完成深入学习中的题目。
时间:8分钟
要求:1、自主探究完成题目
2、不会的题目用笔画出来
1.画出函数y=-6x与y=-6x+5的图象.
二、探究新知
x
-2
-1
0
1
2
y=-6x
y=-6x+5
12
6
0
-6
-12
17
11
5
-1
-7
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
2.观察与比较.
这两个函数的图象形状都是 ,并且倾斜程度 .函数y=6x的图象经过原点,函数y=-6x+5的图象与y轴交于点 ,即它可以看作由直线y=-6x向 平移 个单位长度得到.
比较上面两个函数图象的相同点与不同点.填出你的观察结果并与同伴交流.
一条直线
(0,5)
相同
上
5
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
5.结论.
一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移︱b︱个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移)
完成迁移运用中的题目
时间:7分钟
要求:1、自主探究完成题目
2、不会的题目用笔画出来
3、注意解题步骤的规范性
图象特征
大致图象
K>0
b>0
b=0
b<0
上升,交点在y轴的正半轴。
上升,交点在原点。
上升,交点在y轴的负半轴。
x
y
0
x
y
0
x
y
0
知识归纳
图象特征
大致图象
K<0
b>0
b=0
b<0
下降,交点在y轴的正半轴。
下降,交点在原点。
下降,交点在y轴的负半轴。
x
y
0
x
y
0
x
y
0
知识归纳
课堂小结
这节课我们学到了什么?
完成当堂训练中的题目
时间:7分钟
要求:1、自主探究完成题目
2、不会的题目用笔画出来
3、注意解题步骤的规范性
让我们为激情小组
表示祝贺,
其他小组再接再厉,
永不言输!
