人教版数学七年级下册6.3 实数(2)(共18张)
文档属性
| 名称 | 人教版数学七年级下册6.3 实数(2)(共18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 284.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 13:15:11 | ||
图片预览




文档简介
6.3 实数(2)
你能在数轴上找到表示 这样的无理数的点吗?
一、实数与数轴
每个有理数都可以用数轴上的点表示.无理数是否也可以用数轴上的点表示出来呢?
为什么?
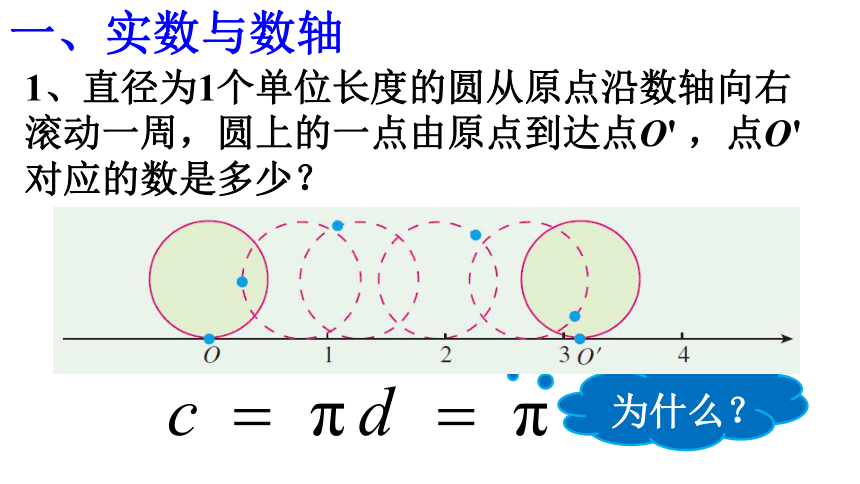
1、直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O' ,点O' 对应的数是多少?
一、实数与数轴
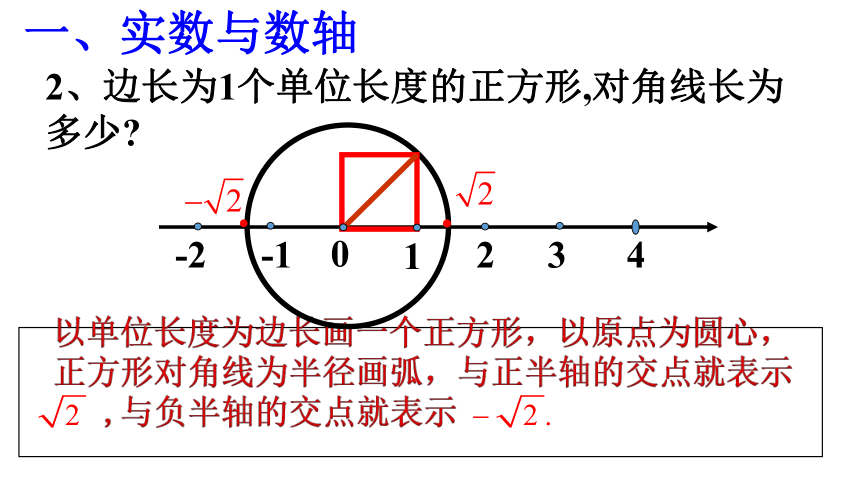
2、边长为1个单位长度的正方形,对角线长为多少?
以单位长度为边长画一个正方形,以原点为圆心,
正方形对角线为半径画弧,与正半轴的交点就表示
,与负半轴的交点就表示
一、实数与数轴
0
1
2
4
3
-1
-2
一、实数与数轴
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数.
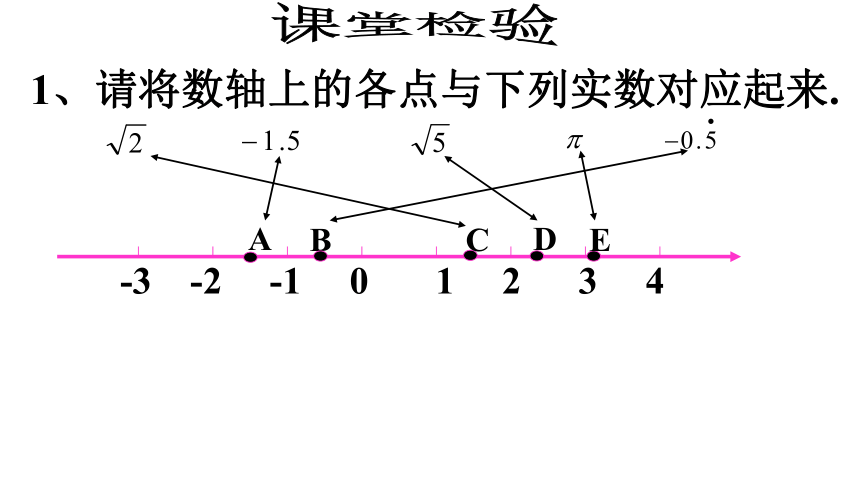
1、请将数轴上的各点与下列实数对应起来.
课堂检验
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
的相反数是 , 的相反数是 ,
0的相反数是 .
二、实数范围内的相反数、倒数、绝对值
3. a 是一个实数 ,它的相反数是 .
4.一个正实数的绝对值是 ;一个负实数的绝对值是 ;0的绝对值是 .
它本身
它的相反数
0
-a
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
二、实数范围内的相反数、倒数、绝对值
例1 (1) 分别写出 的相反数.
3.14
6
-
-
p
,
(2)指出 分别是什么数的相反数;
练习题:
1.
的相反数是 ,
的相反数是
2.
3. P56第3题
1、用字母表示有理数的加法交换律和结合律.
这些运算律对无理数还成立吗?
2、用字母表示有理数的乘法
交换律、乘法结合律、乘法分
配律.
三、实数范围内的运算
成立
例2 计算下列各式的值.
练习题:计算:
三、实数范围内的运算
例3 计算(结果保留小数点后两位):
如果结果要求保留两位小数,中间的计算过程需要保留三位小数.
三、实数范围内的运算
解:(1)
(2)
练习1:
中,无理数的个数是( )
A. 2 B. 3 C. 4 D. 5
B
在下列各数
实数a,b,c,d在数轴上的对应点如图所示,则(1)它们从小到大的顺序是 .
(2)
c d 0 b a
练习2:
3或- 3
(1) 的倒数是 ;
(2) 的绝对值是 ;
(3) 若 ,且xy>0,x+y= .
(4)点A在数轴上表示的数为 ,点B在数轴上表示的数为 ,则A、B两点的距离为 .
练习3:
1.
2.
3.
4.
练习4:
3.实数与数轴上的点是什么关系.
2.实数的定义和分类
1.无理数的定义
课堂小结:
——无限不循环小数叫做无理数。
——按性质分类、按符号分类。
——实数与数轴上的点是一一对应关系。
再长的路,一步步也能走完,
再短的路,不迈开双脚也无法到达。
你能在数轴上找到表示 这样的无理数的点吗?
一、实数与数轴
每个有理数都可以用数轴上的点表示.无理数是否也可以用数轴上的点表示出来呢?
为什么?
1、直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O' ,点O' 对应的数是多少?
一、实数与数轴
2、边长为1个单位长度的正方形,对角线长为多少?
以单位长度为边长画一个正方形,以原点为圆心,
正方形对角线为半径画弧,与正半轴的交点就表示
,与负半轴的交点就表示
一、实数与数轴
0
1
2
4
3
-1
-2
一、实数与数轴
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数.
1、请将数轴上的各点与下列实数对应起来.
课堂检验
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
的相反数是 , 的相反数是 ,
0的相反数是 .
二、实数范围内的相反数、倒数、绝对值
3. a 是一个实数 ,它的相反数是 .
4.一个正实数的绝对值是 ;一个负实数的绝对值是 ;0的绝对值是 .
它本身
它的相反数
0
-a
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
二、实数范围内的相反数、倒数、绝对值
例1 (1) 分别写出 的相反数.
3.14
6
-
-
p
,
(2)指出 分别是什么数的相反数;
练习题:
1.
的相反数是 ,
的相反数是
2.
3. P56第3题
1、用字母表示有理数的加法交换律和结合律.
这些运算律对无理数还成立吗?
2、用字母表示有理数的乘法
交换律、乘法结合律、乘法分
配律.
三、实数范围内的运算
成立
例2 计算下列各式的值.
练习题:计算:
三、实数范围内的运算
例3 计算(结果保留小数点后两位):
如果结果要求保留两位小数,中间的计算过程需要保留三位小数.
三、实数范围内的运算
解:(1)
(2)
练习1:
中,无理数的个数是( )
A. 2 B. 3 C. 4 D. 5
B
在下列各数
实数a,b,c,d在数轴上的对应点如图所示,则(1)它们从小到大的顺序是 .
(2)
c d 0 b a
练习2:
3或- 3
(1) 的倒数是 ;
(2) 的绝对值是 ;
(3) 若 ,且xy>0,x+y= .
(4)点A在数轴上表示的数为 ,点B在数轴上表示的数为 ,则A、B两点的距离为 .
练习3:
1.
2.
3.
4.
练习4:
3.实数与数轴上的点是什么关系.
2.实数的定义和分类
1.无理数的定义
课堂小结:
——无限不循环小数叫做无理数。
——按性质分类、按符号分类。
——实数与数轴上的点是一一对应关系。
再长的路,一步步也能走完,
再短的路,不迈开双脚也无法到达。
