人教版七年级下册数学 5.3.1平行线的性质 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版七年级下册数学 5.3.1平行线的性质 同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 102.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 10:32:19 | ||
图片预览


文档简介
5.3.1平行线的性质
同步练习
一.选择题
1.如图,若直线l1∥l2,则下列各式成立的是( )
A.∠1=∠2
B.∠4=∠5
C.∠2+∠5=180°
D.∠1+∠3=180°
2.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b
B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c
D.∵∠2+∠3=180°,∴a∥c
3.如图,若AB∥CD,则( )
A.∠B=∠1
B.∠A=∠2
C.∠B=∠2
D.∠1=∠2
4.如图,若a∥b,c∥d,∠1=72°,则下列结论错误的是( )
A.∠2=108°
B.∠3=72°
C.∠4=108°
D.∠5=72°
5.如图,AB∥CD,点E在BC上.且CD=CE,若∠B=36°,则∠D的大小为( )
A.36°
B.72°
C.65°
D.67°
6.如图,已知AE∥BC,∠1=∠2,则下列结论不成立的是( )
A.∠B=∠C
B.∠1+∠2=∠B+∠C
C.∠1=∠BAC
D.∠1=∠2=∠B=∠C
7.如图,EG∥AB,FG∥DC,∠B=100°,∠C=120°,∠EGF的度数是( )
A.30°
B.40°
C.45°
D.60°
8.如图,已知∠1=∠2,∠3=50°,则∠4的度数为( )
A.80°
B.70°
C.60°
D.50°
9.如图,l1∥l2,则下列各式中值为180°的是( )
A.α+β+γ
B.α+β﹣γ
C.β+γ﹣α
D.α﹣β+γ
10.已知∠1=120°,∠2=60°,∠3+∠4=180°,如图所示,则在结论①a∥b,②a∥c,③b∥c,④∠3=∠2中,正确的个数是( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图,已知AB∥CD,∠A=36°,∠C=120°,则∠F﹣∠E的大小是
°.
12.如图,直线AB∥CD,∠BAE=27°,∠AEC=79°,则∠DCE=
°.
13.如图,已知AB∥CD,∠ABE=α,∠CDE=β,则∠E=
.
14.已知,如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=70°,则∠BFD=
.
15.如图,点B在MN上,过AB的中点O作MN的平行线,分别交∠ABM的平分线和∠ABN的平分线于点C,D.则∠CBD=
.
三.解答题(共3小题)
16.如图,点P是∠NOM的边OM上一点,PD⊥ON于D,∠OPD=30°,PQ∥ON,试求∠MPQ的度数.
17.如图,点B,C,D在同一条直线上,∠A=∠B.如果CE∥AB,那么∠1=∠2.对以下说理过程填空:
∵CE∥AB(已知),
∴∠1=
(
),
∠2=
(
),
∵∠A=∠B(已知),
∴∠1=∠2
(
).
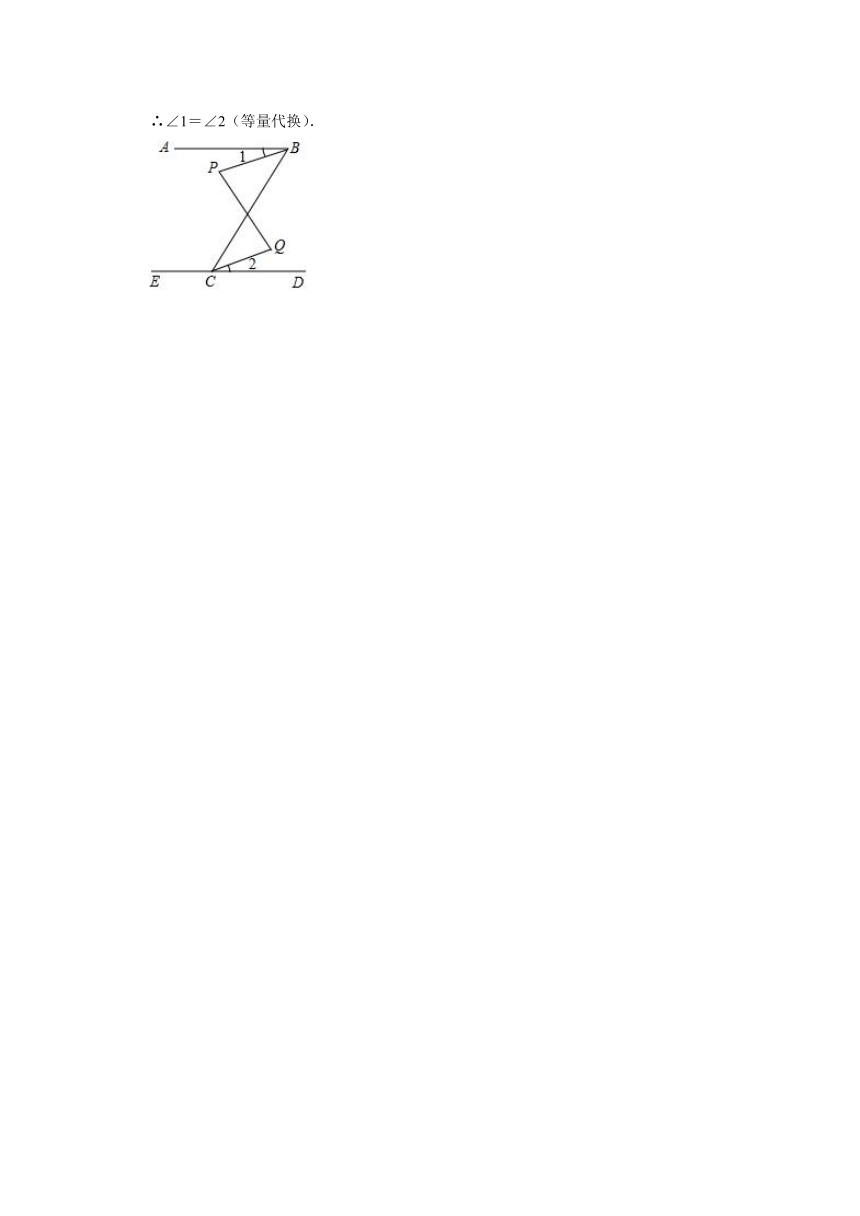
18.如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(
).
∴∠ABC=∠BCD(
).
∵∠P=∠Q(已知),
∴PB∥(
)(
).
∴∠PBC=(
)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(
),∠2=∠BCD﹣(
),
∴∠1=∠2(等量代换).
参考答案
一.选择题
1.解:∵直线l1∥l2,
∴∠1+∠3=180°,∠2+∠4=180°,
故选:D.
2.解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
3.解:∵AB∥CD,
∴∠A=∠1,∠B=∠2.
故选:C.
4.解:如图,
∵c∥d,
∴∠6=∠1=72°,
∴∠2=108°,故A结论正确;
∵a∥b,
∴∠4=∠6=72°,
∴∠3=72°,故B结论正确,C结论错误;
∴∠5=72°,故D结论正确.
故选:C.
5.解:∵AB∥CD,∠B=36°,
∴∠C=∠B=36°,
又∵点E在BC上,且CD=CE,
∴∠D=∠CED,
∴在△CED中,∠C+∠D+∠CED=180°,
∴36°+2∠D=180°,
∴∠D=72°.
故选:B.
6.解:∵AE∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1=∠2,
∴∠B=∠C,∠1+∠2=∠B+∠C,∠1=∠2=∠B=∠C,
∴结论不正确的是∠1=∠BAC.
故选:C.
7.解:
∵EG∥AB,FG∥DC,
∴∠EGB+∠B=180°,∠FGC+∠C=180°,
∵∠B=100°,∠C=120°,
∴∠EGB=80°,∠FGC=60°,
∴∠EGF=180°﹣∠EGB﹣∠FGC=180°﹣80°﹣60°=40°,
故选:B.
8.解:∵∠5=∠2(对顶角相等),∠1=∠2,
∴∠1=∠5,
∴a∥b,
∴∠3=∠4,
∵∠3=50°,
∴∠4=50°.
故选:D.
9.解:∵l1∥l2,
∴∠1=α,
∵∠1=180°﹣β﹣γ,
∴α=180°﹣β﹣γ,
即180°=α+β﹣γ.
故选:B.
10.解:∵∠2=60°,
∴∠5=120°,
∵∠1=120°,
∴a∥c,故②正确;
∵∠4=∠6,∠3+∠4=180°,
∴∠3+∠6=180°,
∴a∥b,故①正确;
∴b∥c,故③正确;
无法得出∠3=∠2,故④错误.
故正确的有3个.
故选:C.
二.填空题
11.解:如图,过点E作EG∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠A=∠1=36°,∠2=∠3,∠4=180°﹣∠C=180°﹣120°=60°
∴∠EFC﹣∠AEF=∠3+∠4﹣∠1﹣∠2=∠4﹣∠1=60°﹣36°=24°.
故答案为:24.
12.解:延长AE交CD于F,
∵AB∥CD,∠BAE=27°,
∴∠AFC=∠BAE=27°,
∵∠AEC=79°,
∴∠ECD=∠AEC﹣∠AFC=79°﹣27°=52°.
故答案为:52.
13.解:如图,延长AB交DE于点F,
∵AB∥CD,
∴∠β=∠BFE.
∵∠α是△BEF的外角,
∴∠α=∠γ+∠BFE,即∠α=∠γ+∠β,
∴∠E=α﹣β.
故答案为:α﹣β.
14.解:如图,过点E作EP∥AB,过F作FM∥AB,
∴AB∥CD∥EP∥FM,
∴∠ABE=∠BEP,∠CDE=∠DEP,∠ABF=∠BFM,∠CDF=∠DFM,
∴∠ABE+∠CDE=∠BED=70°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF+∠CDF=(∠ABE+∠CDE)=35°,
∴∠BFD=35°.
故答案为:35°.
15.解:∵CD平行MN,
∴∠OCB=∠CBM,
∵BC平分∠ABM,
∴∠OBC=∠CBM,
∴∠OCB=∠OBC,
∴OC=OB,
同理可证:OB=OD,
∴OA=OB=OC=OD,
∵CD=OC+OD,
AB=OA+OB,
∴AB=CD,
∴四边形ACBD是矩形,
∴∠CBD=90°,
故答案为:90°.
三.解答题(共3小题)
16.解:∵PD⊥ON于D,∠OPD=30°,
∴∠PDO=90°,
∴∠O=60°,
∵PQ∥ON,
∴∠O=∠MPQ,
∴∠MPQ=60°.
17.解:∵CE∥AB(已知),
∴∠1=∠B(两直线平行,同为角相等),
∠2=∠A(两直线平行,内错角相等),
∵∠A=∠B(已知),
∴∠1=∠2
(等量代换).
故答案为:∠B,两直线平行,同为角相等;∠A,两直线平行,内错角相等;等量代换.
18.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
同步练习
一.选择题
1.如图,若直线l1∥l2,则下列各式成立的是( )
A.∠1=∠2
B.∠4=∠5
C.∠2+∠5=180°
D.∠1+∠3=180°
2.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b
B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c
D.∵∠2+∠3=180°,∴a∥c
3.如图,若AB∥CD,则( )
A.∠B=∠1
B.∠A=∠2
C.∠B=∠2
D.∠1=∠2
4.如图,若a∥b,c∥d,∠1=72°,则下列结论错误的是( )
A.∠2=108°
B.∠3=72°
C.∠4=108°
D.∠5=72°
5.如图,AB∥CD,点E在BC上.且CD=CE,若∠B=36°,则∠D的大小为( )
A.36°
B.72°
C.65°
D.67°
6.如图,已知AE∥BC,∠1=∠2,则下列结论不成立的是( )
A.∠B=∠C
B.∠1+∠2=∠B+∠C
C.∠1=∠BAC
D.∠1=∠2=∠B=∠C
7.如图,EG∥AB,FG∥DC,∠B=100°,∠C=120°,∠EGF的度数是( )
A.30°
B.40°
C.45°
D.60°
8.如图,已知∠1=∠2,∠3=50°,则∠4的度数为( )
A.80°
B.70°
C.60°
D.50°
9.如图,l1∥l2,则下列各式中值为180°的是( )
A.α+β+γ
B.α+β﹣γ
C.β+γ﹣α
D.α﹣β+γ
10.已知∠1=120°,∠2=60°,∠3+∠4=180°,如图所示,则在结论①a∥b,②a∥c,③b∥c,④∠3=∠2中,正确的个数是( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图,已知AB∥CD,∠A=36°,∠C=120°,则∠F﹣∠E的大小是
°.
12.如图,直线AB∥CD,∠BAE=27°,∠AEC=79°,则∠DCE=
°.
13.如图,已知AB∥CD,∠ABE=α,∠CDE=β,则∠E=
.
14.已知,如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=70°,则∠BFD=
.
15.如图,点B在MN上,过AB的中点O作MN的平行线,分别交∠ABM的平分线和∠ABN的平分线于点C,D.则∠CBD=
.
三.解答题(共3小题)
16.如图,点P是∠NOM的边OM上一点,PD⊥ON于D,∠OPD=30°,PQ∥ON,试求∠MPQ的度数.
17.如图,点B,C,D在同一条直线上,∠A=∠B.如果CE∥AB,那么∠1=∠2.对以下说理过程填空:
∵CE∥AB(已知),
∴∠1=
(
),
∠2=
(
),
∵∠A=∠B(已知),
∴∠1=∠2
(
).
18.如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(
).
∴∠ABC=∠BCD(
).
∵∠P=∠Q(已知),
∴PB∥(
)(
).
∴∠PBC=(
)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(
),∠2=∠BCD﹣(
),
∴∠1=∠2(等量代换).
参考答案
一.选择题
1.解:∵直线l1∥l2,
∴∠1+∠3=180°,∠2+∠4=180°,
故选:D.
2.解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
3.解:∵AB∥CD,
∴∠A=∠1,∠B=∠2.
故选:C.
4.解:如图,
∵c∥d,
∴∠6=∠1=72°,
∴∠2=108°,故A结论正确;
∵a∥b,
∴∠4=∠6=72°,
∴∠3=72°,故B结论正确,C结论错误;
∴∠5=72°,故D结论正确.
故选:C.
5.解:∵AB∥CD,∠B=36°,
∴∠C=∠B=36°,
又∵点E在BC上,且CD=CE,
∴∠D=∠CED,
∴在△CED中,∠C+∠D+∠CED=180°,
∴36°+2∠D=180°,
∴∠D=72°.
故选:B.
6.解:∵AE∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1=∠2,
∴∠B=∠C,∠1+∠2=∠B+∠C,∠1=∠2=∠B=∠C,
∴结论不正确的是∠1=∠BAC.
故选:C.
7.解:
∵EG∥AB,FG∥DC,
∴∠EGB+∠B=180°,∠FGC+∠C=180°,
∵∠B=100°,∠C=120°,
∴∠EGB=80°,∠FGC=60°,
∴∠EGF=180°﹣∠EGB﹣∠FGC=180°﹣80°﹣60°=40°,
故选:B.
8.解:∵∠5=∠2(对顶角相等),∠1=∠2,
∴∠1=∠5,
∴a∥b,
∴∠3=∠4,
∵∠3=50°,
∴∠4=50°.
故选:D.
9.解:∵l1∥l2,
∴∠1=α,
∵∠1=180°﹣β﹣γ,
∴α=180°﹣β﹣γ,
即180°=α+β﹣γ.
故选:B.
10.解:∵∠2=60°,
∴∠5=120°,
∵∠1=120°,
∴a∥c,故②正确;
∵∠4=∠6,∠3+∠4=180°,
∴∠3+∠6=180°,
∴a∥b,故①正确;
∴b∥c,故③正确;
无法得出∠3=∠2,故④错误.
故正确的有3个.
故选:C.
二.填空题
11.解:如图,过点E作EG∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠A=∠1=36°,∠2=∠3,∠4=180°﹣∠C=180°﹣120°=60°
∴∠EFC﹣∠AEF=∠3+∠4﹣∠1﹣∠2=∠4﹣∠1=60°﹣36°=24°.
故答案为:24.
12.解:延长AE交CD于F,
∵AB∥CD,∠BAE=27°,
∴∠AFC=∠BAE=27°,
∵∠AEC=79°,
∴∠ECD=∠AEC﹣∠AFC=79°﹣27°=52°.
故答案为:52.
13.解:如图,延长AB交DE于点F,
∵AB∥CD,
∴∠β=∠BFE.
∵∠α是△BEF的外角,
∴∠α=∠γ+∠BFE,即∠α=∠γ+∠β,
∴∠E=α﹣β.
故答案为:α﹣β.
14.解:如图,过点E作EP∥AB,过F作FM∥AB,
∴AB∥CD∥EP∥FM,
∴∠ABE=∠BEP,∠CDE=∠DEP,∠ABF=∠BFM,∠CDF=∠DFM,
∴∠ABE+∠CDE=∠BED=70°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF+∠CDF=(∠ABE+∠CDE)=35°,
∴∠BFD=35°.
故答案为:35°.
15.解:∵CD平行MN,
∴∠OCB=∠CBM,
∵BC平分∠ABM,
∴∠OBC=∠CBM,
∴∠OCB=∠OBC,
∴OC=OB,
同理可证:OB=OD,
∴OA=OB=OC=OD,
∵CD=OC+OD,
AB=OA+OB,
∴AB=CD,
∴四边形ACBD是矩形,
∴∠CBD=90°,
故答案为:90°.
三.解答题(共3小题)
16.解:∵PD⊥ON于D,∠OPD=30°,
∴∠PDO=90°,
∴∠O=60°,
∵PQ∥ON,
∴∠O=∠MPQ,
∴∠MPQ=60°.
17.解:∵CE∥AB(已知),
∴∠1=∠B(两直线平行,同为角相等),
∠2=∠A(两直线平行,内错角相等),
∵∠A=∠B(已知),
∴∠1=∠2
(等量代换).
故答案为:∠B,两直线平行,同为角相等;∠A,两直线平行,内错角相等;等量代换.
18.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
