青岛版五四制 四年级数学下册3.3质数与合数 教案
文档属性
| 名称 | 青岛版五四制 四年级数学下册3.3质数与合数 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 68.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览



文档简介
质数和合数
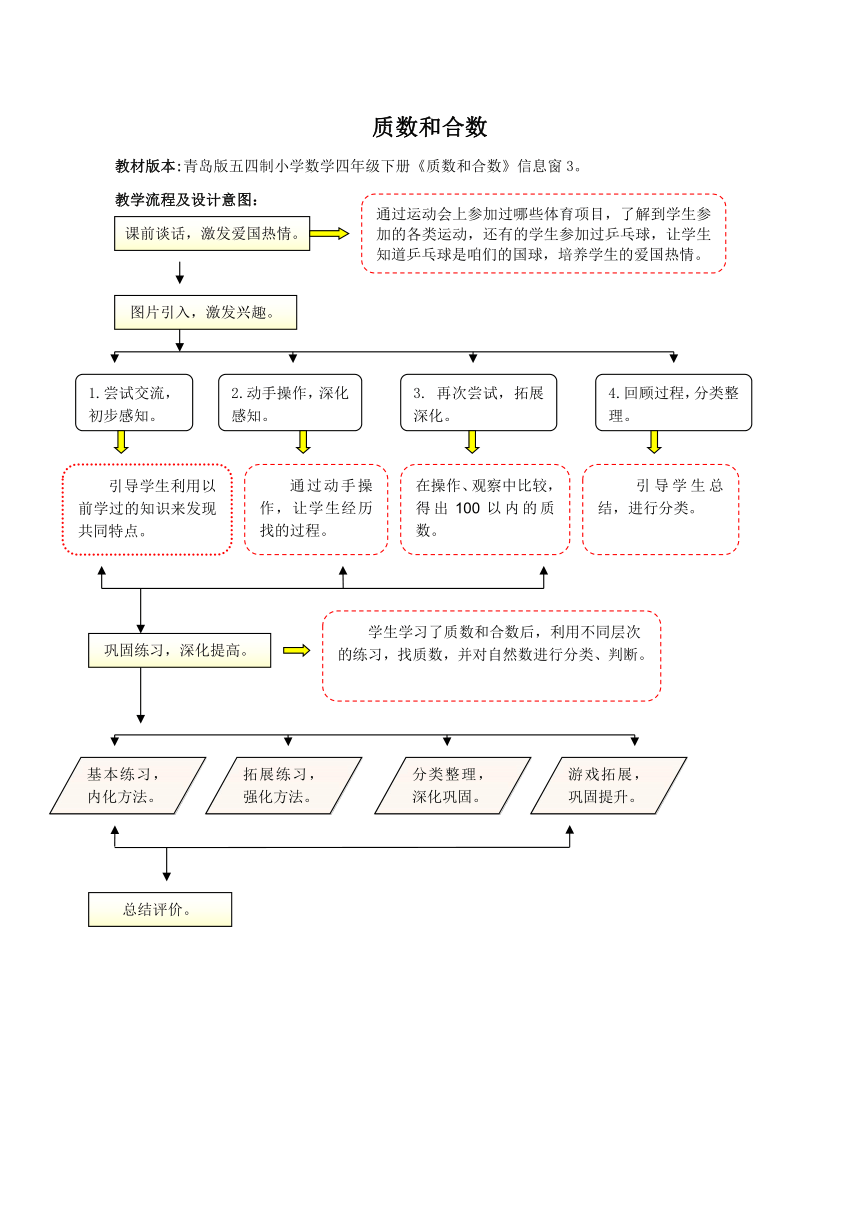
教材版本:青岛版五四制小学数学四年级下册《质数和合数》信息窗3。
教学流程及设计意图:
《质数和合数》教学设计
【教学内容】五四制青岛版小学数学四年级下册第50页的信息窗3
【教学目标】
结合具体情境,理解质数和合数的意义。
在探索新知的过程中,实现对学生进行分类思想、极限思想的渗透。
通过活动,激发学生学习的兴趣,体现数学的价值。
【教学重难点】
重、难点:通过列举,理解质数和合数的意义。
【教学准备】
学具教具:多媒体课件、自制磁力教具等。
【教学理念】
“作为知识的数学出校门不到两年学生就可能忘了,唯有深深铭记在头脑中的数学的精神、数学的思想、研究方法和着眼点等,这些随时随地发生作用,使他们终身受益。”本节课我在使学生理解和掌握质数和合数的意义这一目标的同时,实现对学生渗透某些数学思想的任务,如分类的思想、极限的思想等。
【教学过程】
一、开放课堂,引导学生初步感知
1.情境引入
师:你们参加过运动会吗?都参加过哪些运动项目?成绩咋样?
师:今天老师给大家带来了一些运动会前大型团体操表演的图片,想看吗?
(出示信息窗)
师:仔细观察,你能发现哪些数学信息?(学生边说边板书)40、25、35、24、32
师:1组我们称1号方队。
师:刚才提到“方队”,方队是什么意思?
方队就是两排或两排以上的正方形或长方形的队伍。
师:这些数有什么特点?看来这个问题对于大家有点难度,提示一下:找一找这些数的因数都有哪一些?并且数一数它们的因数的个数,请同学们自主完成完成学习单1
师:谁来说一下你找的因数?
板书:40:8个,25:3个,35:4个,24:6个,32:6个
师:这些数能排成方队,再看它们的因数的个数都在2个以上。是不是只有因数的个数在2个以上的才能排成方队呢?仅凭这几个数得出结论还不够,还需要利用大量的例子进行验证。
2.动手验证
师:你想验证几?
师:数学讲究有序思考,咱们从1、2、3------来验证可以吗?找一找这些数都有哪些因数?并且数一数因数的个数,并判断能否排成方队。
请同学们以小组为单位利用你手中的卡片通过摆一摆,完成学习单2
数字 有哪些因数 因数的个数 能否摆成方队
1
2
3
4
5
6
7
8
9
10
------
师:哪个小组愿意第一个把你们的想法交流一下?
(两个学生合作,边摆边交流)
师:(小结)通过刚才的交流,我们知道像4、6、8、9、10这些数,它们的因数的个数都在2个以上,它们也都能排成方队,这再次验证了只有因数的个数在2个以上的才能排成方队。
【设计意图】借助学生身边熟悉的生活,常见的队列队形为载体来学习质数和合数,是在现实生活中找到一个重要的数学模型。学生在分析问题的过程中,明确了是否能排成方队与一个数因数的个数有关,初步感受到质数合数的本质,从而引入新课的学习。
二、动手实践,引导学生寻找质数
1.完善概念
师:像这样,一个数除了1和它2个因数外,还有别的因数的数,咱们叫它合数;一个数除了1和它本身外,再没有别的因数的数叫质数。(板书:质数和合数)这就是我们这节课要研究的质数和合数。
师:1是什么数?为什么?
师:谁能根据你的理解说说什么是质数?什么是合数?
2.寻找100以内的质数
师:合作的力量是巨大的,咱们继续加大难度,找一找100以内的质数怎么样?
师:(出示百数表)这是一张百数表,咱们怎么做能又快又对的找出100以内的质数?
生:分工
师:就按你说的办法,咱们分一下工,一组找11-20的质数,二组找21-30的质数,三组找31-40的质数------。除了这些以外,在找的过程中你还有没有要提醒大家的?
生:把2、3、5、7的倍数划去,剩下的就是质数。
师:用不用找8、9、10的倍数?11用不用找?为什么?
师:咱们来汇报一下你们小组的合作成果
师:同学们找的还真不错!
3.列举质数的例子
师:通过大家的合作,咱们很快找出了100以内的质数,你能举一个有关质数的例子?
学生举例
4.练习
师:刚才大家举了这么多例子,程老师也想举几个例子
练习:最小的质数是( );最小的合数是( );最大的质数是( );最大的合数是( );1是质数还是合数?
【设计意图】这一环节以活动的形式,既活跃了课堂气氛,使枯燥的教学富有朝气,又扩展了学生的参与面。特别是在小组合作的基础上找出100以内的质数,学生活动的积极性很高,而且在整个找的过程中,学生的思维一直处于“扬”的过程,相信这对孩子今后的自主学习非常有帮助。
三、归纳提升,引导学生进行分类
师:我们知道,自然数按是否被2整除,我们把自然数分为奇数和偶数。
师:自然数如果按因数的个数可以怎样分呢?(1,质数,合数)
【设计意图】这一环节的设置是在学生理解和掌握质数和合数的意义这一目标的同时,实现对学生渗透分类的思想。在学生对自然数的分类时,学生最初没把“1”单独作为一部分,这是学生的最初的想法,因为“1”就只有一个数,而质数和合数有那么多。可是从分类的角度出发,尽管“1”只有一个数,可它代表着一类数,类与类之间是平等的。
四、拓展内化,引导学生巩固发展
师:一节课的时间马上就要结束了,咱们这节课主要研究了质数和合数。咱们来轻松一下,做个小游戏好吗?
规则:例如,学号是质数的起立,你要大声报出你的学号,同学们判断是不是质数,如果同学们认为你报的对,那你就可以出去休息了,如果报的不对,可就要被留下了。听明白了?
师:学号是质数的起立
师:学号是合数的起立
师:咋就剩下你自己了?(1)
师:嗯,我明白了,你的学号既不是质数也不是合数。
【设计意图】本环节是在上一问题基础上思维层次的提高,让学生从身边的学号思考质数和合数,既是对这节新授课的巩固提升,又让学生感受到数学就在我们的身边。
教材版本:青岛版五四制小学数学四年级下册《质数和合数》信息窗3。
教学流程及设计意图:
《质数和合数》教学设计
【教学内容】五四制青岛版小学数学四年级下册第50页的信息窗3
【教学目标】
结合具体情境,理解质数和合数的意义。
在探索新知的过程中,实现对学生进行分类思想、极限思想的渗透。
通过活动,激发学生学习的兴趣,体现数学的价值。
【教学重难点】
重、难点:通过列举,理解质数和合数的意义。
【教学准备】
学具教具:多媒体课件、自制磁力教具等。
【教学理念】
“作为知识的数学出校门不到两年学生就可能忘了,唯有深深铭记在头脑中的数学的精神、数学的思想、研究方法和着眼点等,这些随时随地发生作用,使他们终身受益。”本节课我在使学生理解和掌握质数和合数的意义这一目标的同时,实现对学生渗透某些数学思想的任务,如分类的思想、极限的思想等。
【教学过程】
一、开放课堂,引导学生初步感知
1.情境引入
师:你们参加过运动会吗?都参加过哪些运动项目?成绩咋样?
师:今天老师给大家带来了一些运动会前大型团体操表演的图片,想看吗?
(出示信息窗)
师:仔细观察,你能发现哪些数学信息?(学生边说边板书)40、25、35、24、32
师:1组我们称1号方队。
师:刚才提到“方队”,方队是什么意思?
方队就是两排或两排以上的正方形或长方形的队伍。
师:这些数有什么特点?看来这个问题对于大家有点难度,提示一下:找一找这些数的因数都有哪一些?并且数一数它们的因数的个数,请同学们自主完成完成学习单1
师:谁来说一下你找的因数?
板书:40:8个,25:3个,35:4个,24:6个,32:6个
师:这些数能排成方队,再看它们的因数的个数都在2个以上。是不是只有因数的个数在2个以上的才能排成方队呢?仅凭这几个数得出结论还不够,还需要利用大量的例子进行验证。
2.动手验证
师:你想验证几?
师:数学讲究有序思考,咱们从1、2、3------来验证可以吗?找一找这些数都有哪些因数?并且数一数因数的个数,并判断能否排成方队。
请同学们以小组为单位利用你手中的卡片通过摆一摆,完成学习单2
数字 有哪些因数 因数的个数 能否摆成方队
1
2
3
4
5
6
7
8
9
10
------
师:哪个小组愿意第一个把你们的想法交流一下?
(两个学生合作,边摆边交流)
师:(小结)通过刚才的交流,我们知道像4、6、8、9、10这些数,它们的因数的个数都在2个以上,它们也都能排成方队,这再次验证了只有因数的个数在2个以上的才能排成方队。
【设计意图】借助学生身边熟悉的生活,常见的队列队形为载体来学习质数和合数,是在现实生活中找到一个重要的数学模型。学生在分析问题的过程中,明确了是否能排成方队与一个数因数的个数有关,初步感受到质数合数的本质,从而引入新课的学习。
二、动手实践,引导学生寻找质数
1.完善概念
师:像这样,一个数除了1和它2个因数外,还有别的因数的数,咱们叫它合数;一个数除了1和它本身外,再没有别的因数的数叫质数。(板书:质数和合数)这就是我们这节课要研究的质数和合数。
师:1是什么数?为什么?
师:谁能根据你的理解说说什么是质数?什么是合数?
2.寻找100以内的质数
师:合作的力量是巨大的,咱们继续加大难度,找一找100以内的质数怎么样?
师:(出示百数表)这是一张百数表,咱们怎么做能又快又对的找出100以内的质数?
生:分工
师:就按你说的办法,咱们分一下工,一组找11-20的质数,二组找21-30的质数,三组找31-40的质数------。除了这些以外,在找的过程中你还有没有要提醒大家的?
生:把2、3、5、7的倍数划去,剩下的就是质数。
师:用不用找8、9、10的倍数?11用不用找?为什么?
师:咱们来汇报一下你们小组的合作成果
师:同学们找的还真不错!
3.列举质数的例子
师:通过大家的合作,咱们很快找出了100以内的质数,你能举一个有关质数的例子?
学生举例
4.练习
师:刚才大家举了这么多例子,程老师也想举几个例子
练习:最小的质数是( );最小的合数是( );最大的质数是( );最大的合数是( );1是质数还是合数?
【设计意图】这一环节以活动的形式,既活跃了课堂气氛,使枯燥的教学富有朝气,又扩展了学生的参与面。特别是在小组合作的基础上找出100以内的质数,学生活动的积极性很高,而且在整个找的过程中,学生的思维一直处于“扬”的过程,相信这对孩子今后的自主学习非常有帮助。
三、归纳提升,引导学生进行分类
师:我们知道,自然数按是否被2整除,我们把自然数分为奇数和偶数。
师:自然数如果按因数的个数可以怎样分呢?(1,质数,合数)
【设计意图】这一环节的设置是在学生理解和掌握质数和合数的意义这一目标的同时,实现对学生渗透分类的思想。在学生对自然数的分类时,学生最初没把“1”单独作为一部分,这是学生的最初的想法,因为“1”就只有一个数,而质数和合数有那么多。可是从分类的角度出发,尽管“1”只有一个数,可它代表着一类数,类与类之间是平等的。
四、拓展内化,引导学生巩固发展
师:一节课的时间马上就要结束了,咱们这节课主要研究了质数和合数。咱们来轻松一下,做个小游戏好吗?
规则:例如,学号是质数的起立,你要大声报出你的学号,同学们判断是不是质数,如果同学们认为你报的对,那你就可以出去休息了,如果报的不对,可就要被留下了。听明白了?
师:学号是质数的起立
师:学号是合数的起立
师:咋就剩下你自己了?(1)
师:嗯,我明白了,你的学号既不是质数也不是合数。
【设计意图】本环节是在上一问题基础上思维层次的提高,让学生从身边的学号思考质数和合数,既是对这节新授课的巩固提升,又让学生感受到数学就在我们的身边。
