北师大数学八年级下册1.1三角形全等和等腰三角形的性质教案
文档属性
| 名称 | 北师大数学八年级下册1.1三角形全等和等腰三角形的性质教案 |  | |
| 格式 | zip | ||
| 文件大小 | 206.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 19:05:51 | ||
图片预览

文档简介
等腰三角形的性质
教材定位分析:
1、教学内容:
本节课是义务教育课程标准实验教材数学八年级上册第十三章第三节《等腰三角形》的第一课时的内容——等腰三角形的性质,等腰三角形是一种特殊的三角形,它除了具有一般三角形的性质以外,还具有一些特殊的性质。它是轴对称图形,具有对称性,本节课就是要利用对称的知识来研究等腰三角形的有关性质,并利用全等三角形的知识证明这些性质。
2、在教材中的地位与作用:
本节课是在学生掌握了一般三角形和轴对称的知识,具有初步的推理证明能力的基础上进行学习的,担负着进一步训练学生学会分析、学会证明的任务,在培养学生的思维能力和推理能力等方面有重要的作用;而“等边对等角”和“三线合一”的性质是今后论证两个角相等、两条线段相等、两条直线垂直的重要依据,本节课是第三课时研究等边三角形的基础,是全章的重点之一。
?
二、教学定位:
教学目标:
1、知识与技能
①理解掌握等腰三角形的性质.
②运用等腰三角形的性质进行计算和证明.
2、过程与方法?
①
经历“操作-观察-发现-归纳-证明-应用”的知识形成过程,培养学生的分析推理及解决问题能力.
②培养学生“转化”的数学思想、应用意识及合作学习的能力。
情感与态度?
①鼓励学生积极参与数学活动,激发学生的求知欲.
②体会数学与生活的密切联系.
重点、难点:等腰三角形的性质及应用
教学过程设计:
环节一:情景引入
1、观察图片,有什么共同特点?
你知道什么是等腰三角形吗?
等腰三角形的定义:有两条边相等的三角形叫做等腰三角形。
环节二:理性提升
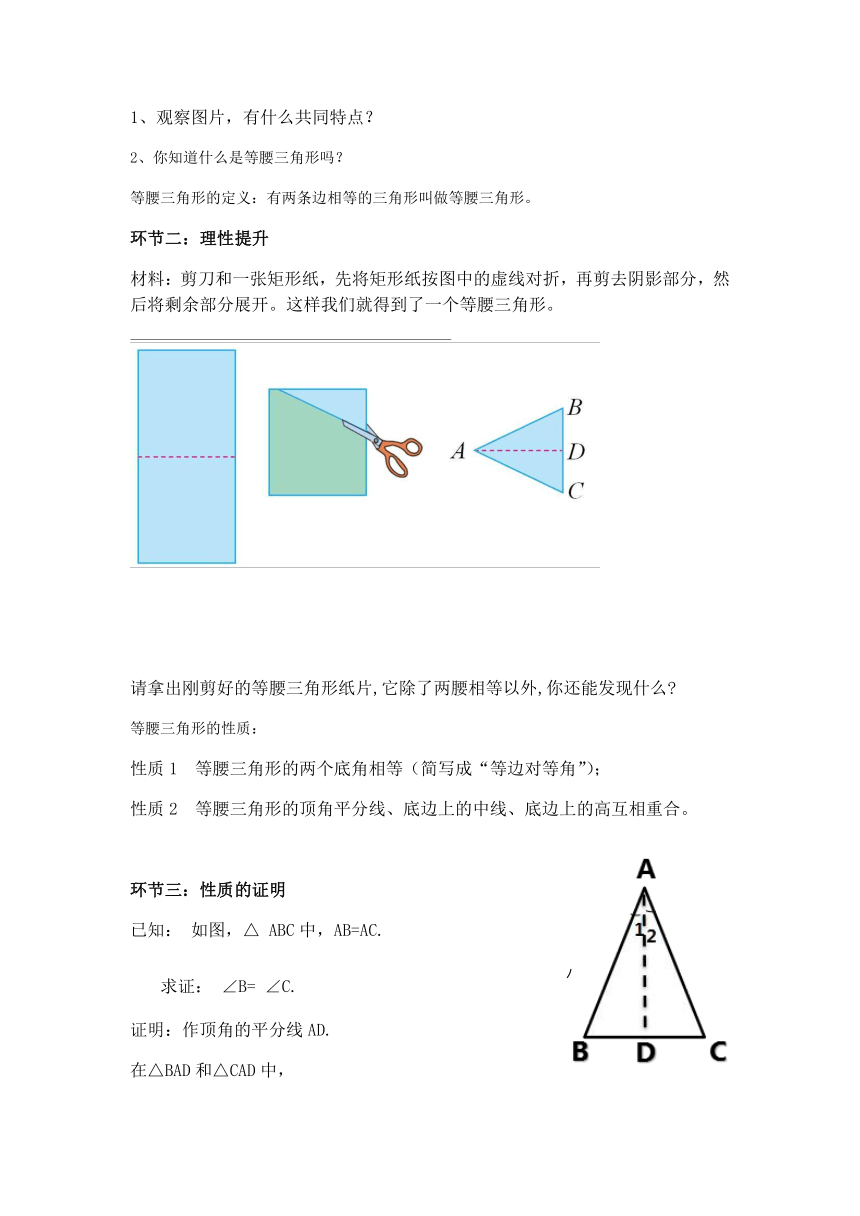
材料:剪刀和一张矩形纸,先将矩形纸按图中的虚线对折,再剪去阴影部分,然后将剩余部分展开。这样我们就得到了一个等腰三角形。
请拿出刚剪好的等腰三角形纸片,它除了两腰相等以外,你还能发现什么?
等腰三角形的性质:
性质1
等腰三角形的两个底角相等(简写成“等边对等角”);
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
环节三:性质的证明
已知:
如图,△
ABC中,AB=AC.
求证:
∠B=
∠C.
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC
(
已知
),∠
1=
∠
2
,
AD=AD
(公共边)
,∴
△BAD
≌
△CAD
(SAS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
你还有其他方法证明性质1吗?
还可以作底边的高线或底边上的中线。
由两个三角形全等可知∠BAD=∠CAD,即AD为顶角∠BAC的平分线,∠ADC=
∠ADB两角相加又为180度所以∠ADC=
∠ADB=900
即AD为底边BC上的高。由此也可证出等腰三角形的另一个性质。
环节四:性质应用
例1
在三角形ABC中,已知AB=AC,且∠B=80°
,则∠C=
___度,∠A=____度?
解:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80°
(已知)
∴∠C=80°
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∴∠A=180°-
∠B-∠C
∠A=20°
随堂练习:在三角形ABC中,AB=AC,且AD
⊥BC,已知BD=2cm,求DC=___cm,
BC=___cm?
解:∵
AB=AC
,AD
⊥BC(已知)
∴BD=CD(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm,BC=4cm
环节五:课堂小结
等腰三角形的性质定理:
1、等腰三角形的两个底角相等。
(简写成“等边对等角”)
2、等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)
教师微反思:等腰三角形在初中几何里很基础也很常见,其中等腰三角形的性质在实际的应用中非常普遍,尤其是“三线合一”这一重要定理.根据新的教育理念,以轴对称图形为切入点,在学生动手的基础上,通过学生观察猜想,自主探究、证明等方式学习,以获取知识。
教材定位分析:
1、教学内容:
本节课是义务教育课程标准实验教材数学八年级上册第十三章第三节《等腰三角形》的第一课时的内容——等腰三角形的性质,等腰三角形是一种特殊的三角形,它除了具有一般三角形的性质以外,还具有一些特殊的性质。它是轴对称图形,具有对称性,本节课就是要利用对称的知识来研究等腰三角形的有关性质,并利用全等三角形的知识证明这些性质。
2、在教材中的地位与作用:
本节课是在学生掌握了一般三角形和轴对称的知识,具有初步的推理证明能力的基础上进行学习的,担负着进一步训练学生学会分析、学会证明的任务,在培养学生的思维能力和推理能力等方面有重要的作用;而“等边对等角”和“三线合一”的性质是今后论证两个角相等、两条线段相等、两条直线垂直的重要依据,本节课是第三课时研究等边三角形的基础,是全章的重点之一。
?
二、教学定位:
教学目标:
1、知识与技能
①理解掌握等腰三角形的性质.
②运用等腰三角形的性质进行计算和证明.
2、过程与方法?
①
经历“操作-观察-发现-归纳-证明-应用”的知识形成过程,培养学生的分析推理及解决问题能力.
②培养学生“转化”的数学思想、应用意识及合作学习的能力。
情感与态度?
①鼓励学生积极参与数学活动,激发学生的求知欲.
②体会数学与生活的密切联系.
重点、难点:等腰三角形的性质及应用
教学过程设计:
环节一:情景引入
1、观察图片,有什么共同特点?
你知道什么是等腰三角形吗?
等腰三角形的定义:有两条边相等的三角形叫做等腰三角形。
环节二:理性提升
材料:剪刀和一张矩形纸,先将矩形纸按图中的虚线对折,再剪去阴影部分,然后将剩余部分展开。这样我们就得到了一个等腰三角形。
请拿出刚剪好的等腰三角形纸片,它除了两腰相等以外,你还能发现什么?
等腰三角形的性质:
性质1
等腰三角形的两个底角相等(简写成“等边对等角”);
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
环节三:性质的证明
已知:
如图,△
ABC中,AB=AC.
求证:
∠B=
∠C.
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC
(
已知
),∠
1=
∠
2
,
AD=AD
(公共边)
,∴
△BAD
≌
△CAD
(SAS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
你还有其他方法证明性质1吗?
还可以作底边的高线或底边上的中线。
由两个三角形全等可知∠BAD=∠CAD,即AD为顶角∠BAC的平分线,∠ADC=
∠ADB两角相加又为180度所以∠ADC=
∠ADB=900
即AD为底边BC上的高。由此也可证出等腰三角形的另一个性质。
环节四:性质应用
例1
在三角形ABC中,已知AB=AC,且∠B=80°
,则∠C=
___度,∠A=____度?
解:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80°
(已知)
∴∠C=80°
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∴∠A=180°-
∠B-∠C
∠A=20°
随堂练习:在三角形ABC中,AB=AC,且AD
⊥BC,已知BD=2cm,求DC=___cm,
BC=___cm?
解:∵
AB=AC
,AD
⊥BC(已知)
∴BD=CD(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm,BC=4cm
环节五:课堂小结
等腰三角形的性质定理:
1、等腰三角形的两个底角相等。
(简写成“等边对等角”)
2、等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)
教师微反思:等腰三角形在初中几何里很基础也很常见,其中等腰三角形的性质在实际的应用中非常普遍,尤其是“三线合一”这一重要定理.根据新的教育理念,以轴对称图形为切入点,在学生动手的基础上,通过学生观察猜想,自主探究、证明等方式学习,以获取知识。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
