人教版数学八年级下册 第18章 18.1平行四边形同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级下册 第18章 18.1平行四边形同步测试试题(一)(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 199.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览



文档简介
平行四边形同步测试试题(一)
一.选择题
1.如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠BCF
B.∠B=∠F
C.AC=CF
D.AD=CF
2.已知,一个平行四边形相邻两边的长分别是2和3,则它的周长是( )
A.6
B.7
C.8
D.10
3.?ABCD中,∠B=50°,则∠C=( )
A.40°
B.50°
C.130°
D.140°
4.如图,四边形ABCD的对角线AC,BD相交于点O,AO=CO.添加下列条件能判定四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC
B.∠BAD=∠BCD
C.AB=CD
D.AD=BC
5.已知?ABCD的对角线AC、BD相交于点O,△AOD是等边三角形,且AD=1,则AB等于( )
A.2
B.4
C.2
D.
6.如图,平行四边形ABCD的周长是56cm,△ACD的周长是36cm,则AC的长为( )
A.6cm
B.12cm
C.4cm
D.8cm
7.如图,在平行四边形ABCD中,已知∠ODA=90°,AC=20,BD=12,E、F分别是线段OD、OA的中点,则EF的长为( )
A.3
B.4
C.5
D.8
8.如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB向右平移个单位长度得到△A'B'C'.若AB=13,AC=12,B'C'=5,则平行四边形ACC'A'的面积为( )
A.10
B.14
C.15
D.30
9.如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
10.如图,在?ABCD中,BE平分∠ABC,交AD于点E,AE=3,ED=1,则ABCD的周长为( )
A.10
B.12
C.14
D.16
二.填空题
11.在?ABCD中,∠C:∠D=5:4,则∠B的度数为
.
12.如图,平行四边形ABCD中AB=6cm,周长是28cm,则AD=
cm.
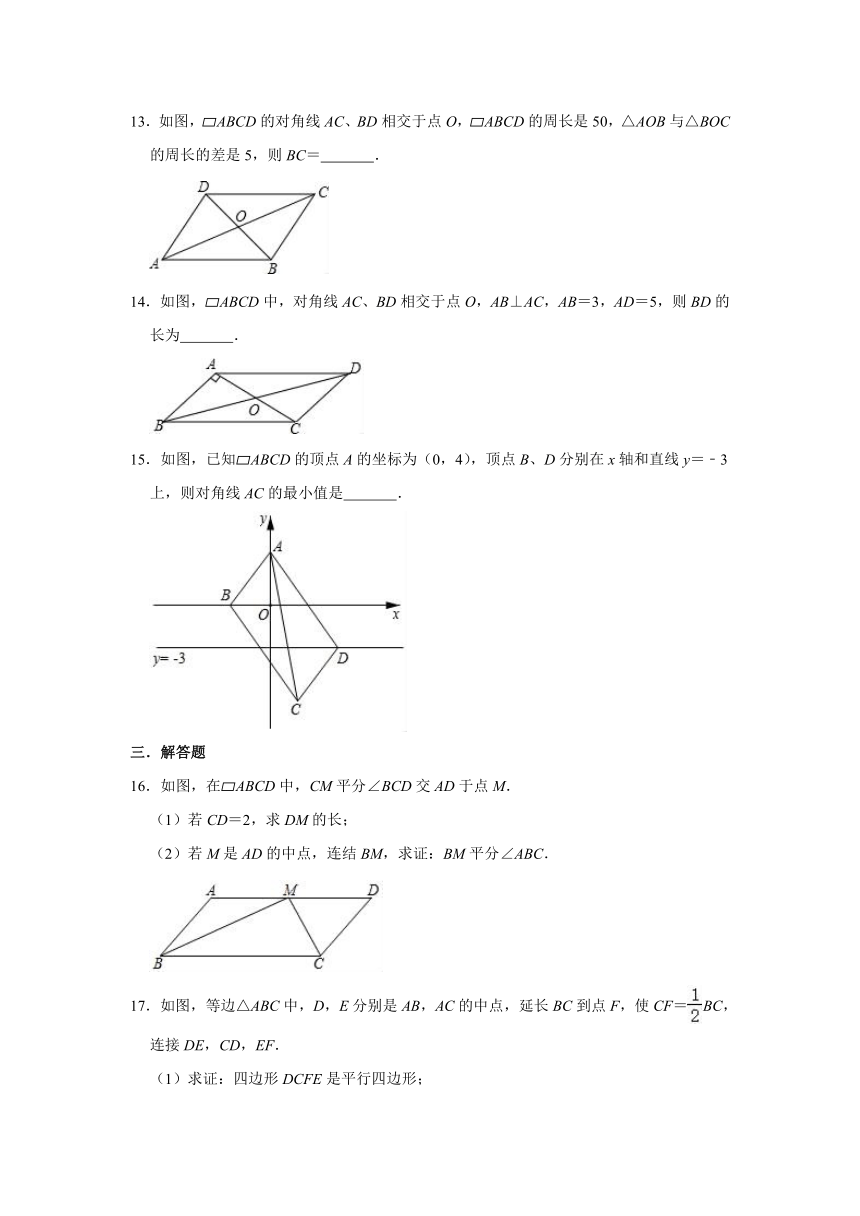
13.如图,?ABCD的对角线AC、BD相交于点O,?ABCD的周长是50,△AOB与△BOC的周长的差是5,则BC=
.
14.如图,?ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长为
.
15.如图,已知?ABCD的顶点A的坐标为(0,4),顶点B、D分别在x轴和直线y=﹣3上,则对角线AC的最小值是
.
三.解答题
16.如图,在?ABCD中,CM平分∠BCD交AD于点M.
(1)若CD=2,求DM的长;
(2)若M是AD的中点,连结BM,求证:BM平分∠ABC.
17.如图,等边△ABC中,D,E分别是AB,AC的中点,延长BC到点F,使CF=BC,连接DE,CD,EF.
(1)求证:四边形DCFE是平行四边形;
(2)若等边△ABC的边长为6,求EF的长.
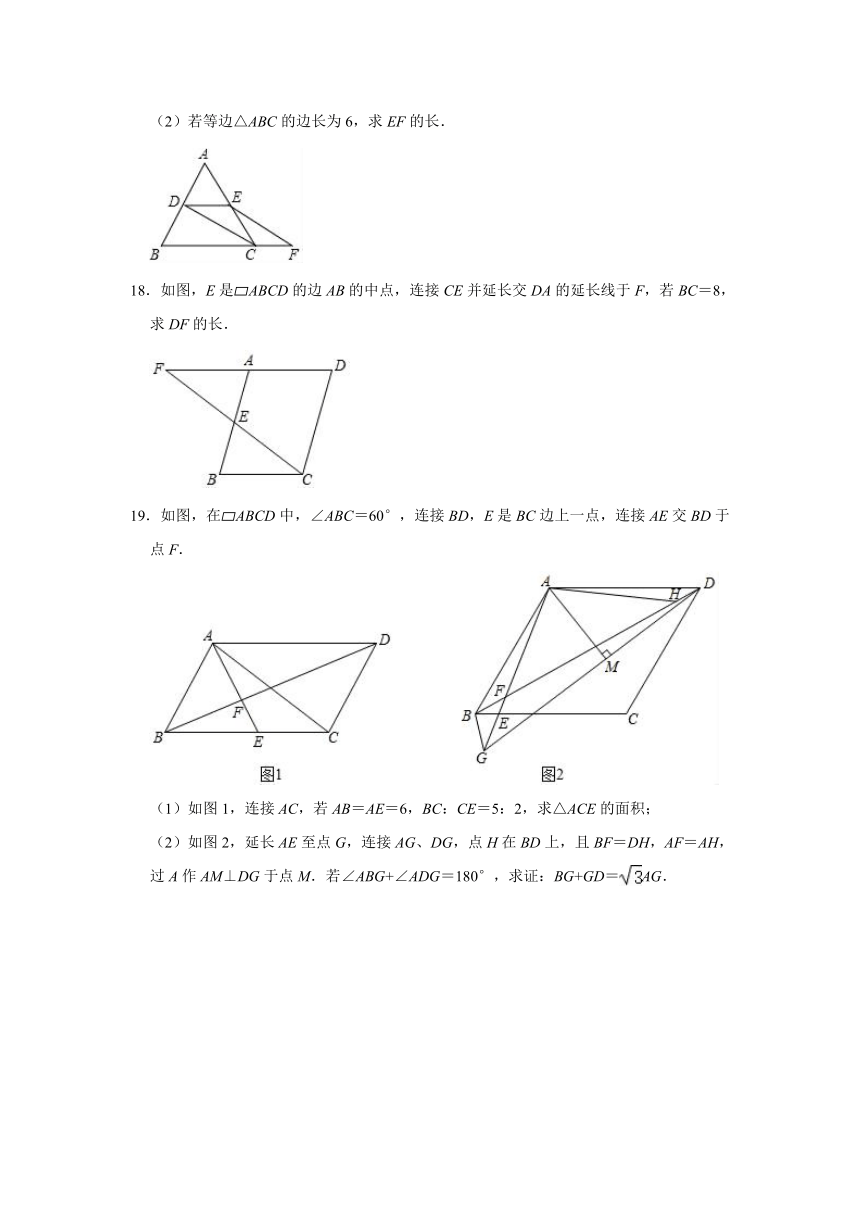
18.如图,E是?ABCD的边AB的中点,连接CE并延长交DA的延长线于F,若BC=8,求DF的长.
19.如图,在?ABCD中,∠ABC=60°,连接BD,E是BC边上一点,连接AE交BD于点F.
(1)如图1,连接AC,若AB=AE=6,BC:CE=5:2,求△ACE的面积;
(2)如图2,延长AE至点G,连接AG、DG,点H在BD上,且BF=DH,AF=AH,过A作AM⊥DG于点M.若∠ABG+∠ADG=180°,求证:BG+GD=AG.
参考答案与试题解析
一.选择题
1.【解答】解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,DE=AC,
A、∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
B、根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
C、根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D、根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
故选:A.
2.【解答】解:∵一个平行四边形相邻两边的长分别是2和3,
∴它的周长=2×(2+3)=10,
故选:D.
3.【解答】解:∵?ABCD中,∠B=50°,
∴AB∥CD,
∴∠C=180°﹣∠B=180°﹣50°=130°,
故选:C.
4.【解答】解:添加∠ABD=∠BDC,能判定四边形ABCD是平行四边形,理由如下:
在△AOB和△COD中,,
∴△AOB≌△COD(AAS),
∴OB=OD,
又∵AO=CO,
∴四边形ABCD是平行四边形;
故选:A.
5.【解答】解:∵△AOD是等边三角形,
∴AD=OA=OD=1,
∵四边形ABCD是平行四边形,
∴OA=AC,OD=BD,
∴AC=BD=2,
∴四边形ABCD是矩形,
在Rt△ABD中,AB===,
故选:D.
6.【解答】解:∵?ABCD的周长为56cm,
∴AB+BC=28cm,
∵△ACD的周长是36cm,
∴AC=36﹣28=8cm,
故选:D.
7.【解答】解:∵在平行四边形ABCD中,∠ODA=90°,AC=20,BD=12,
∴AO=CO=10,BO=DO=6,
故AD=,
∵E、F分别是线段OD、OA的中点,
∴EF是△ADO的中位线,
∴EF∥AD,EF=AD,
则EF的长为:4.
故选:B.
8.【解答】解:如图所示,过C作CD⊥AB于D,
由平移可得,B'C'=BC=5,
∵∠ACB=90°,AB=13,AC=12,
∴AC×BC=AB×CD,
∴CD==,
∵△ABC沿直线AB向右平移个单位长度得到△A'B'C',
∴AA'=,
∴平行四边形ACC'A'的面积=AA'×CD=×=15,
故选:C.
9.【解答】解:∵点D和点E分别是BC和BA的中点,
∴DE是△ABC的中位线,
∴DE=AC=×4=2,
故选:B.
10.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵DE=1,
∴AD=BC=4,
∴平行四边形ABCD的周长是2(3+4)=14.
故选:C.
二.填空题(共5小题)
11.【解答】解:在?ABCD中,AD∥BC,∠B=∠D,
∴∠C+∠D=180°,
∵∠C:∠D=5:4,
∴∠C=100°,∠D=80°,
∴∠B=80°.
故答案为80°.
12.【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=6cm,AD=BC,
∵平行四边形ABCD的周长是28cm,
∴AD+AB=14cm,
∴AD=8cm;
故答案为:8.
13.【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵△AOB与△BOC的周长的差是5,
∴AB+OB+OA﹣(BC+OB+OC)=AB﹣BC=5①,
∵?ABCD的周长是50,
∴AB+BC=25②,
∴由①②得:AB=15,BC=10,
故答案为:10.
14.【解答】解:∵?ABCD的对角线AC与BD相交于点O,
∴BO=DO,OA=OC,BC=AD=5,
∵AB⊥AC,AB=3,
∴AC==4,
∴OA=2,
∴BO==,
∴BD=2BO=2.
故答案为:2.
15.【解答】解:设点C坐标为(a,b),
∵顶点B、D分别在x轴和直线y=﹣3上,
∴点B,点D的纵坐标分别为0,﹣3,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴,
∴b=﹣7,
∴点C在直线y=﹣7上运动,
∴当AC⊥直线y=﹣7时,AC的长度有最小值,
∴对角线AC的最小值=4﹣(﹣7)=11,
故答案为:11.
三.解答题(共4小题)
16.【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BCM=∠DMC,
∵CM平分∠BCD,
∴∠BCM=∠DCM,
∴∠DMC=∠DCM,
∴DM=DC=2;
(2)如图,延长BA,CM,交于点E,则∠AME=∠DMC,
∵BE∥CD,
∴∠D=∠EAM,∠E=∠DCM,
∵M是AD的中点,
∴DM=AM,
∴△CDM≌△EAM(ASA),
∴EM=CM,
∵CM平分∠BCD,
∴∠BCM=∠DCM,
∴∠E=∠BCM,
∴BE=BC,
∴BM平分∠ABC.
解法二:由(1)可得,CD=MD,
∵M是AD的中点,
∴DM=AM,
又∵AB=CD,
∴AB=AM,
∴∠ABM=∠AMB,
∵AD∥BC,
∴∠CBM=∠AMB,
∴∠ABM=∠CBM,
∴BM平分∠ABC.
17.【解答】(1)证明:∵点D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=CF,
又∵DE∥CF,
∴四边形DCFE是平行四边形.
(2)解:由(1)得:四边形DCFE是平行四边形,
∴EF=DC.
∵△ABC是等边三角形,
∴AB=BC=6,
∵D为AB的中点,
∴CD⊥AB,BD=AB=×6=3,
在Rt△BCD中,BC=6,
∴CD===3,
∴EF=DC=3.
18.【解答】解:∵E是?ABCD的边AB的中点,
∴AE=BE,∵四边形ABCD是平行四边形,
∴AD=CB=8,AD∥CB,
∴∠F=∠BCE,
在△AEF和△BEC中,,
∴△AEF≌△BEC(AAS),
∴AF=CB=8,
∴DF=AD+AF=16.
19.【解答】解:(1)过A点作AM⊥BE于点M,
∵AB=AE=6,
∴BM=ME=,
∵∠ABC=60°,
∴∠BAM=30°,
∴,
∴,
∵BC:CE=5:2,
∴CE=,
∴;
(2)∵AF=AH,
∴∠AFH=∠AHF,
∴∠AFB=∠AHD,
∵BF=DH,
∴△ABF≌△ADH(SAS),
∴AB=AD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ABC=60°,
∴∠BAD=120°,
将△ABG绕点A逆时针旋转120°,得△ADG′,则∠DAG′=∠BAG,∠ADG′=∠ABG,BG=DG′,AG=AG′,
∵∠ABG+∠ADG=180°,
∴∠ADG′+∠ADG=180°,
∴G、D、G′三点共线,
∴GG′=GD+DG′=DG+BG,
∵∠GAD+∠DAG′=∠GAD+∠BAG,
∴∠GAG′=∠BAD=120°,
∴∠AGG′=∠AG′G=30°,
∵AM⊥GG′,
∴GM=G′M,AM=,
∴GM=,
∴,
∴BG+GD=AG.
一.选择题
1.如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠BCF
B.∠B=∠F
C.AC=CF
D.AD=CF
2.已知,一个平行四边形相邻两边的长分别是2和3,则它的周长是( )
A.6
B.7
C.8
D.10
3.?ABCD中,∠B=50°,则∠C=( )
A.40°
B.50°
C.130°
D.140°
4.如图,四边形ABCD的对角线AC,BD相交于点O,AO=CO.添加下列条件能判定四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC
B.∠BAD=∠BCD
C.AB=CD
D.AD=BC
5.已知?ABCD的对角线AC、BD相交于点O,△AOD是等边三角形,且AD=1,则AB等于( )
A.2
B.4
C.2
D.
6.如图,平行四边形ABCD的周长是56cm,△ACD的周长是36cm,则AC的长为( )
A.6cm
B.12cm
C.4cm
D.8cm
7.如图,在平行四边形ABCD中,已知∠ODA=90°,AC=20,BD=12,E、F分别是线段OD、OA的中点,则EF的长为( )
A.3
B.4
C.5
D.8
8.如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB向右平移个单位长度得到△A'B'C'.若AB=13,AC=12,B'C'=5,则平行四边形ACC'A'的面积为( )
A.10
B.14
C.15
D.30
9.如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
10.如图,在?ABCD中,BE平分∠ABC,交AD于点E,AE=3,ED=1,则ABCD的周长为( )
A.10
B.12
C.14
D.16
二.填空题
11.在?ABCD中,∠C:∠D=5:4,则∠B的度数为
.
12.如图,平行四边形ABCD中AB=6cm,周长是28cm,则AD=
cm.
13.如图,?ABCD的对角线AC、BD相交于点O,?ABCD的周长是50,△AOB与△BOC的周长的差是5,则BC=
.
14.如图,?ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长为
.
15.如图,已知?ABCD的顶点A的坐标为(0,4),顶点B、D分别在x轴和直线y=﹣3上,则对角线AC的最小值是
.
三.解答题
16.如图,在?ABCD中,CM平分∠BCD交AD于点M.
(1)若CD=2,求DM的长;
(2)若M是AD的中点,连结BM,求证:BM平分∠ABC.
17.如图,等边△ABC中,D,E分别是AB,AC的中点,延长BC到点F,使CF=BC,连接DE,CD,EF.
(1)求证:四边形DCFE是平行四边形;
(2)若等边△ABC的边长为6,求EF的长.
18.如图,E是?ABCD的边AB的中点,连接CE并延长交DA的延长线于F,若BC=8,求DF的长.
19.如图,在?ABCD中,∠ABC=60°,连接BD,E是BC边上一点,连接AE交BD于点F.
(1)如图1,连接AC,若AB=AE=6,BC:CE=5:2,求△ACE的面积;
(2)如图2,延长AE至点G,连接AG、DG,点H在BD上,且BF=DH,AF=AH,过A作AM⊥DG于点M.若∠ABG+∠ADG=180°,求证:BG+GD=AG.
参考答案与试题解析
一.选择题
1.【解答】解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,DE=AC,
A、∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
B、根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
C、根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D、根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
故选:A.
2.【解答】解:∵一个平行四边形相邻两边的长分别是2和3,
∴它的周长=2×(2+3)=10,
故选:D.
3.【解答】解:∵?ABCD中,∠B=50°,
∴AB∥CD,
∴∠C=180°﹣∠B=180°﹣50°=130°,
故选:C.
4.【解答】解:添加∠ABD=∠BDC,能判定四边形ABCD是平行四边形,理由如下:
在△AOB和△COD中,,
∴△AOB≌△COD(AAS),
∴OB=OD,
又∵AO=CO,
∴四边形ABCD是平行四边形;
故选:A.
5.【解答】解:∵△AOD是等边三角形,
∴AD=OA=OD=1,
∵四边形ABCD是平行四边形,
∴OA=AC,OD=BD,
∴AC=BD=2,
∴四边形ABCD是矩形,
在Rt△ABD中,AB===,
故选:D.
6.【解答】解:∵?ABCD的周长为56cm,
∴AB+BC=28cm,
∵△ACD的周长是36cm,
∴AC=36﹣28=8cm,
故选:D.
7.【解答】解:∵在平行四边形ABCD中,∠ODA=90°,AC=20,BD=12,
∴AO=CO=10,BO=DO=6,
故AD=,
∵E、F分别是线段OD、OA的中点,
∴EF是△ADO的中位线,
∴EF∥AD,EF=AD,
则EF的长为:4.
故选:B.
8.【解答】解:如图所示,过C作CD⊥AB于D,
由平移可得,B'C'=BC=5,
∵∠ACB=90°,AB=13,AC=12,
∴AC×BC=AB×CD,
∴CD==,
∵△ABC沿直线AB向右平移个单位长度得到△A'B'C',
∴AA'=,
∴平行四边形ACC'A'的面积=AA'×CD=×=15,
故选:C.
9.【解答】解:∵点D和点E分别是BC和BA的中点,
∴DE是△ABC的中位线,
∴DE=AC=×4=2,
故选:B.
10.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵DE=1,
∴AD=BC=4,
∴平行四边形ABCD的周长是2(3+4)=14.
故选:C.
二.填空题(共5小题)
11.【解答】解:在?ABCD中,AD∥BC,∠B=∠D,
∴∠C+∠D=180°,
∵∠C:∠D=5:4,
∴∠C=100°,∠D=80°,
∴∠B=80°.
故答案为80°.
12.【解答】解:∵四边形ABCD是平行四边形,
∴CD=AB=6cm,AD=BC,
∵平行四边形ABCD的周长是28cm,
∴AD+AB=14cm,
∴AD=8cm;
故答案为:8.
13.【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵△AOB与△BOC的周长的差是5,
∴AB+OB+OA﹣(BC+OB+OC)=AB﹣BC=5①,
∵?ABCD的周长是50,
∴AB+BC=25②,
∴由①②得:AB=15,BC=10,
故答案为:10.
14.【解答】解:∵?ABCD的对角线AC与BD相交于点O,
∴BO=DO,OA=OC,BC=AD=5,
∵AB⊥AC,AB=3,
∴AC==4,
∴OA=2,
∴BO==,
∴BD=2BO=2.
故答案为:2.
15.【解答】解:设点C坐标为(a,b),
∵顶点B、D分别在x轴和直线y=﹣3上,
∴点B,点D的纵坐标分别为0,﹣3,
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴,
∴b=﹣7,
∴点C在直线y=﹣7上运动,
∴当AC⊥直线y=﹣7时,AC的长度有最小值,
∴对角线AC的最小值=4﹣(﹣7)=11,
故答案为:11.
三.解答题(共4小题)
16.【解答】解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BCM=∠DMC,
∵CM平分∠BCD,
∴∠BCM=∠DCM,
∴∠DMC=∠DCM,
∴DM=DC=2;
(2)如图,延长BA,CM,交于点E,则∠AME=∠DMC,
∵BE∥CD,
∴∠D=∠EAM,∠E=∠DCM,
∵M是AD的中点,
∴DM=AM,
∴△CDM≌△EAM(ASA),
∴EM=CM,
∵CM平分∠BCD,
∴∠BCM=∠DCM,
∴∠E=∠BCM,
∴BE=BC,
∴BM平分∠ABC.
解法二:由(1)可得,CD=MD,
∵M是AD的中点,
∴DM=AM,
又∵AB=CD,
∴AB=AM,
∴∠ABM=∠AMB,
∵AD∥BC,
∴∠CBM=∠AMB,
∴∠ABM=∠CBM,
∴BM平分∠ABC.
17.【解答】(1)证明:∵点D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=CF,
又∵DE∥CF,
∴四边形DCFE是平行四边形.
(2)解:由(1)得:四边形DCFE是平行四边形,
∴EF=DC.
∵△ABC是等边三角形,
∴AB=BC=6,
∵D为AB的中点,
∴CD⊥AB,BD=AB=×6=3,
在Rt△BCD中,BC=6,
∴CD===3,
∴EF=DC=3.
18.【解答】解:∵E是?ABCD的边AB的中点,
∴AE=BE,∵四边形ABCD是平行四边形,
∴AD=CB=8,AD∥CB,
∴∠F=∠BCE,
在△AEF和△BEC中,,
∴△AEF≌△BEC(AAS),
∴AF=CB=8,
∴DF=AD+AF=16.
19.【解答】解:(1)过A点作AM⊥BE于点M,
∵AB=AE=6,
∴BM=ME=,
∵∠ABC=60°,
∴∠BAM=30°,
∴,
∴,
∵BC:CE=5:2,
∴CE=,
∴;
(2)∵AF=AH,
∴∠AFH=∠AHF,
∴∠AFB=∠AHD,
∵BF=DH,
∴△ABF≌△ADH(SAS),
∴AB=AD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ABC=60°,
∴∠BAD=120°,
将△ABG绕点A逆时针旋转120°,得△ADG′,则∠DAG′=∠BAG,∠ADG′=∠ABG,BG=DG′,AG=AG′,
∵∠ABG+∠ADG=180°,
∴∠ADG′+∠ADG=180°,
∴G、D、G′三点共线,
∴GG′=GD+DG′=DG+BG,
∵∠GAD+∠DAG′=∠GAD+∠BAG,
∴∠GAG′=∠BAD=120°,
∴∠AGG′=∠AG′G=30°,
∵AM⊥GG′,
∴GM=G′M,AM=,
∴GM=,
∴,
∴BG+GD=AG.
