2021年人教版数学八年级数学下册 18.1.1 平行四边形(1)(Word版 无答案)
文档属性
| 名称 | 2021年人教版数学八年级数学下册 18.1.1 平行四边形(1)(Word版 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 95.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览


文档简介
平行四边形
【总结解题方法
提升解题能力】
【知识汇总】
1.平行四边形:两组对边分别平行的四边形.记作:“□”
2.平行四边形的性质:对边相等,对角相等,对角线互相平分,对角线分成的4个三角形面积相等.
3.平行四边形的判定:①根据定义判定(定义法、边的方向)
②两组对边分别相等的四边形是平行四边形(边的方向)
③两组对角分别相等的四边形是平行四边形(角的方向)
④对角线互相平分的四边形是平行四边形
(对角线的方向)
⑤一组对边平行且相等的四边形是平行四边形(边的方向)
4.平行线之间的距离:一条直线上任意一点到另一条直线的距离(处处相等)
5.三角形的中位线:①定义:连接三角形两边中点的线段.
②定理:三角形的中位线平行于三角形的第三边并且等于第三边的一半.(注意逆定理的运用)
【基础夯实】
考点一:平行四边形的性质
1.如图,在□ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
A.1
cm
B.2
cm
C.3
cm
D.4
cm
2.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,
则∠A的大小为(
)
A.150°
B.130°
C.120°
D.100°
3.如图,在□ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4
cm
B.5
cm
C.6
cm
D.8
cm
4.如图,□ABCD的周长为20cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4cm
B.6cm
C.8cm
D.10cm
5.如图,在□ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
A.2
B.3
C.4
D.6
6.如图,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且□ABCD的周长为40,则□ABCD的面积为( )
A.24
B.36
C.40
D.48
7.如图,在□ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x的取值范围是
.
8.平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为
cm.
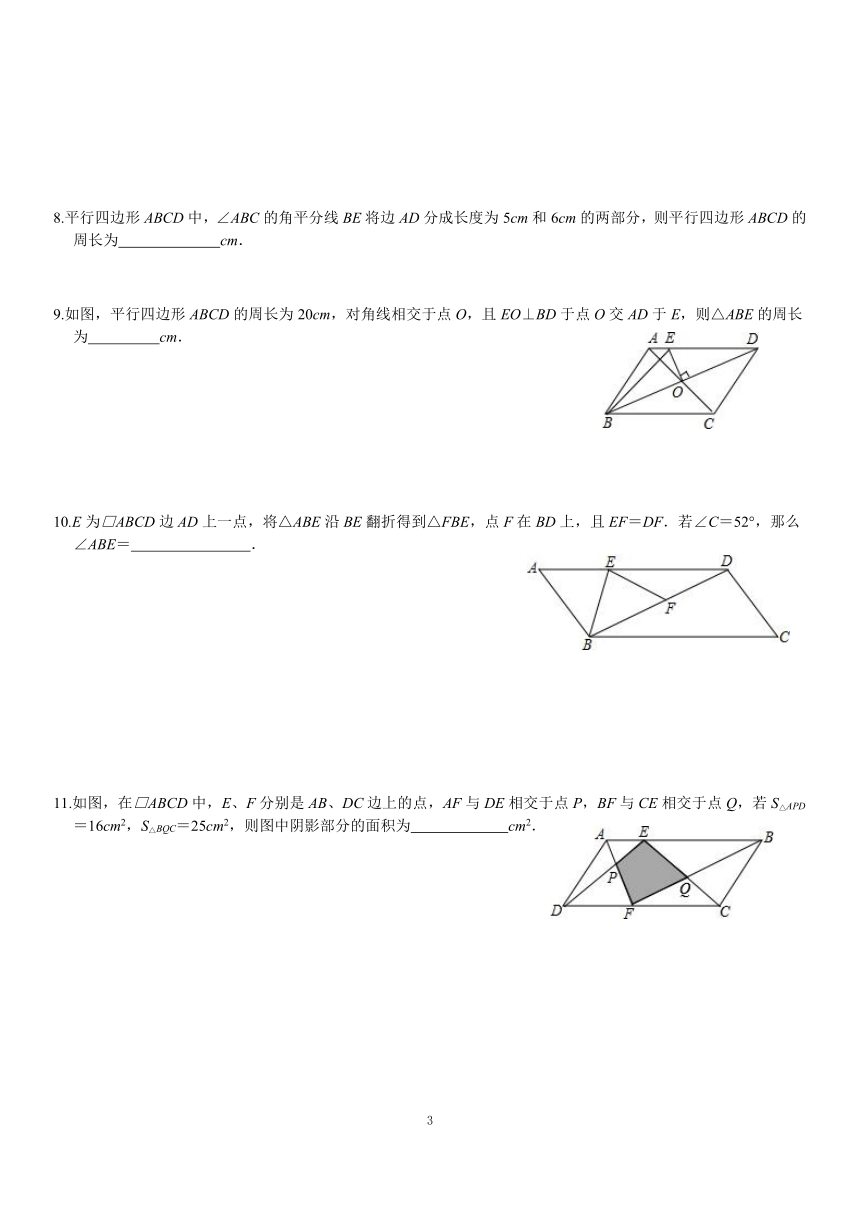
9.如图,平行四边形ABCD的周长为20cm,对角线相交于点O,且EO⊥BD于点O交AD于E,则△ABE的周长为
cm.
10.E为□ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=
.
11.如图,在□ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为
cm2.
12.如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=
s时,以A、C、E、F为顶点四边形是平行四边形.
考点二:三角形的中位线
13.若三角形的三条中位线长分别为2cm,3cm,4cm,则原三角形的周长为( )
A.4.5cm
B.18cm
C.9cm
D.36cm
14.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
A.8
B.10
C.12
D.16
15.如图,四边形ABCD中,∠A=90°,AB=,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3
B.4
C.4.5
D.5
16.如图,△ABC中,AB=7,AC=11,AD平分∠BAC,BD⊥AD,E是BC的中点,那么DE=
17.在△ABC中,D为AB的中点,E为AC上一点,CE=AC,BE、CD交于点O,BE=5cm,则OE=
cm.
【能力拓展】
18.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为
.
【课后巩固】
1.如图,已知□ABCD中,AB=4,BC=6,BC边上的高AE=2,求AF的长.
2.如图,□ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,求AB的长
3.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,求EF的长.
4.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,求PQ的长.
1
【总结解题方法
提升解题能力】
【知识汇总】
1.平行四边形:两组对边分别平行的四边形.记作:“□”
2.平行四边形的性质:对边相等,对角相等,对角线互相平分,对角线分成的4个三角形面积相等.
3.平行四边形的判定:①根据定义判定(定义法、边的方向)
②两组对边分别相等的四边形是平行四边形(边的方向)
③两组对角分别相等的四边形是平行四边形(角的方向)
④对角线互相平分的四边形是平行四边形
(对角线的方向)
⑤一组对边平行且相等的四边形是平行四边形(边的方向)
4.平行线之间的距离:一条直线上任意一点到另一条直线的距离(处处相等)
5.三角形的中位线:①定义:连接三角形两边中点的线段.
②定理:三角形的中位线平行于三角形的第三边并且等于第三边的一半.(注意逆定理的运用)
【基础夯实】
考点一:平行四边形的性质
1.如图,在□ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
A.1
cm
B.2
cm
C.3
cm
D.4
cm
2.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,
则∠A的大小为(
)
A.150°
B.130°
C.120°
D.100°
3.如图,在□ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4
cm
B.5
cm
C.6
cm
D.8
cm
4.如图,□ABCD的周长为20cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4cm
B.6cm
C.8cm
D.10cm
5.如图,在□ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )
A.2
B.3
C.4
D.6
6.如图,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且□ABCD的周长为40,则□ABCD的面积为( )
A.24
B.36
C.40
D.48
7.如图,在□ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x的取值范围是
.
8.平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为
cm.
9.如图,平行四边形ABCD的周长为20cm,对角线相交于点O,且EO⊥BD于点O交AD于E,则△ABE的周长为
cm.
10.E为□ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=
.
11.如图,在□ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为
cm2.
12.如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=
s时,以A、C、E、F为顶点四边形是平行四边形.
考点二:三角形的中位线
13.若三角形的三条中位线长分别为2cm,3cm,4cm,则原三角形的周长为( )
A.4.5cm
B.18cm
C.9cm
D.36cm
14.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
A.8
B.10
C.12
D.16
15.如图,四边形ABCD中,∠A=90°,AB=,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3
B.4
C.4.5
D.5
16.如图,△ABC中,AB=7,AC=11,AD平分∠BAC,BD⊥AD,E是BC的中点,那么DE=
17.在△ABC中,D为AB的中点,E为AC上一点,CE=AC,BE、CD交于点O,BE=5cm,则OE=
cm.
【能力拓展】
18.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为
.
【课后巩固】
1.如图,已知□ABCD中,AB=4,BC=6,BC边上的高AE=2,求AF的长.
2.如图,□ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,求AB的长
3.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,求EF的长.
4.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,求PQ的长.
1
