中位数与众数

(共15张PPT)
知识目标：（1）理解平均数、中位数和众数的含义．
（2）掌握平均数、中位数和众数的计算方法
能力目标： 会计算一组数据的平均数，会确定一组较简
单数据的中位数和众数，培养学生独立思考
勇于创新，小组协作能力
情感目标：通过各中真实、贴近生活的素材和问题情景
激发学生学习数学的热情和兴趣．体验事物
的多面性和学会全面分析事物的必要性．在
合作学习中，学会交流， 相互评价，提高合
作意识能力．
教学目标
重点：掌握中位数、众数的数据代表的概念
难点：选择恰当的数据代表对数据作出判断
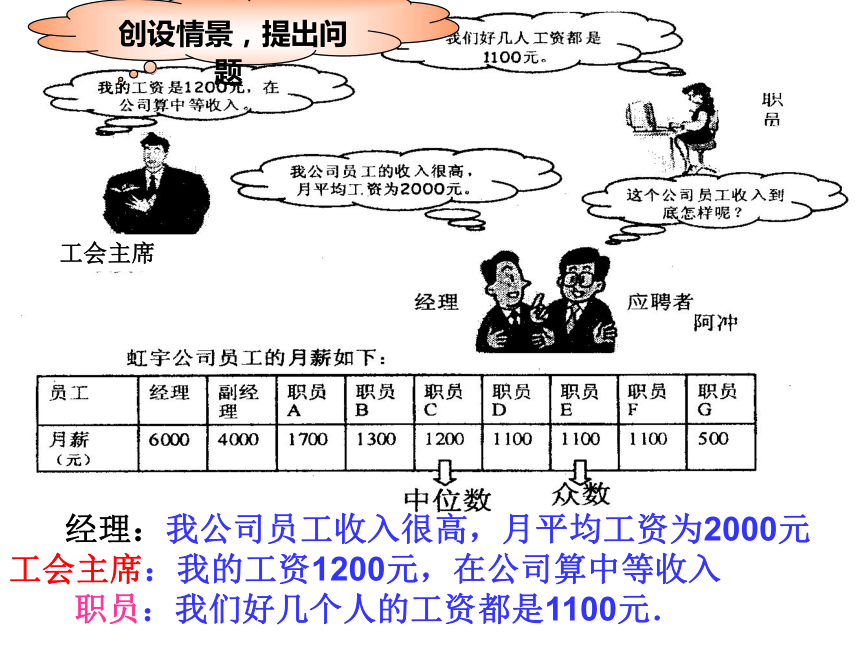
经理：我公司员工收入很高，月平均工资为2000元
工会主席：我的工资1200元，在公司算中等收入
职员：我们好几个人的工资都是1100元．
创设情景，提出问题
工会主席
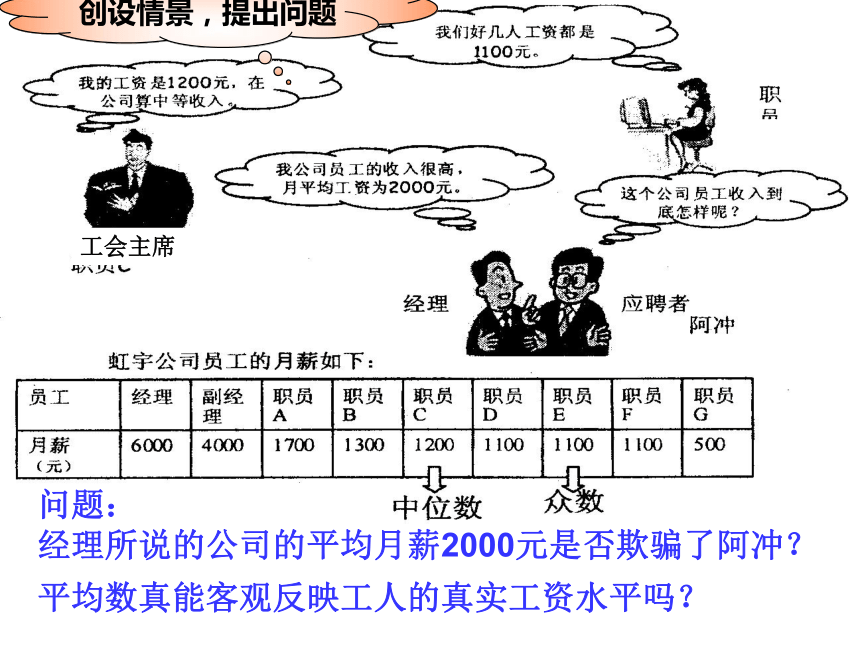
问题：
经理所说的公司的平均月薪2000元是否欺骗了阿冲？
平均数真能客观反映工人的真实工资水平吗？
创设情景，提出问题
工会主席
平均数真能客观反映工人的真实工资水平吗？
四人小组讨论交流，互换观点想法．
工会主席
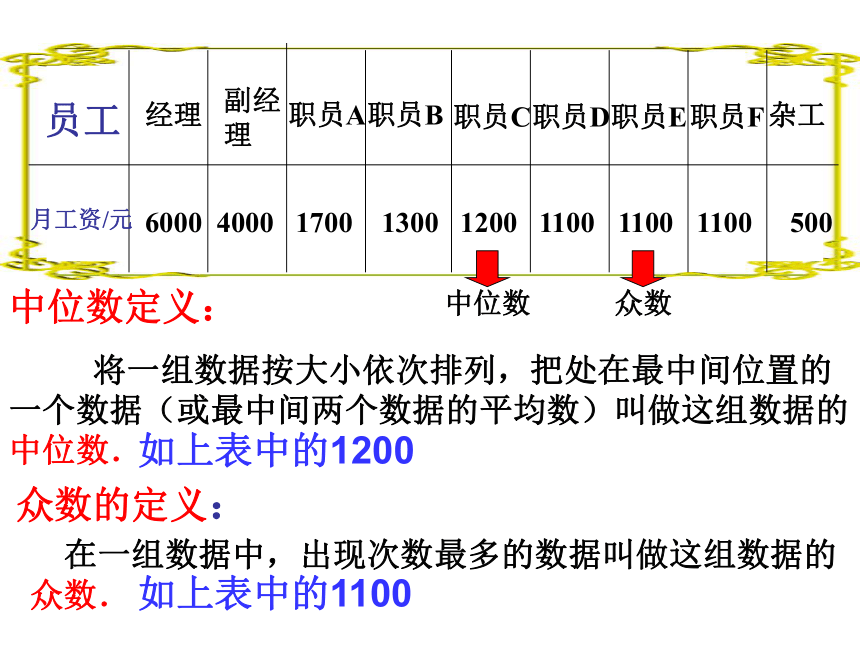
中位数定义：
将一组数据按大小依次排列，把处在最中间位置的一个数据（或最中间两个数据的平均数）叫做这组数据的中位数．
员工
月工资/元
经理
副经 理
职员A
职员B
职员F
职员E
职员D
职员C
杂工
6000
4000
1700
1300
1200
1100
1100
1100
500
众数的定义：
在一组数据中，出现次数最多的数据叫做这组数据的众数．
如上表中的1200
如上表中的1100
中位数
众数
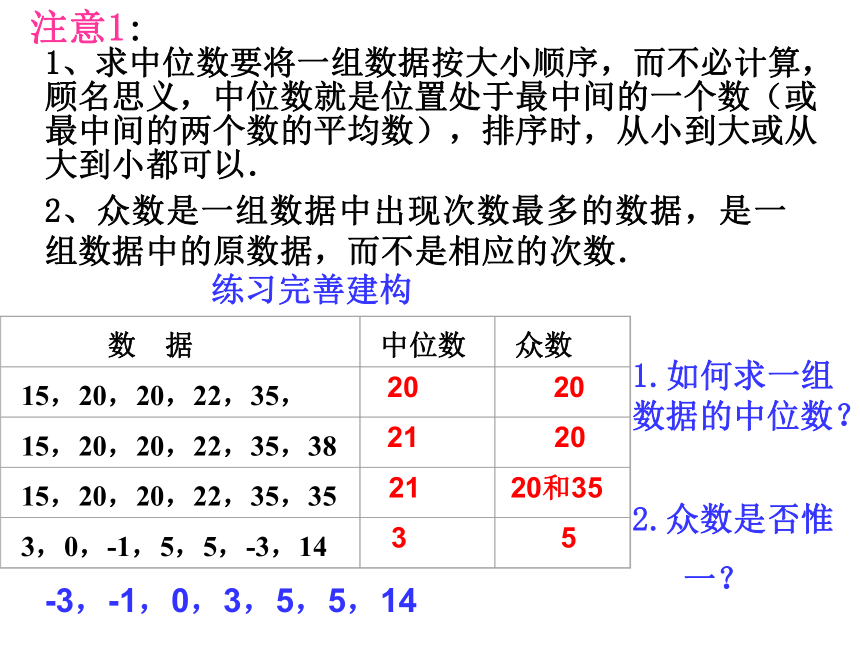
注意1:
2、众数是一组数据中出现次数最多的数据，是一组数据中的原数据，而不是相应的次数．
1、求中位数要将一组数据按大小顺序，而不必计算，顾名思义，中位数就是位置处于最中间的一个数（或最中间的两个数的平均数），排序时，从小到大或从大到小都可以．
数 据
中位数
众数
15，20，20，22，35，


15，20，20，22，35，38


15，20，20，22，35，35


3，0，-1，5，5，-3，14


练习完善建构
1.如何求一组数据的中位数？
2.众数是否惟
一？
20
21
21
-3，-1，0，3，5，5，14
3
20
20
20和35
5
注意2： 1.一组数据中的众数有时不只一个，如数据2、3、－1、2、1、3中，2和3都出现了2次，它们都是这组数据的众数．
2．当数据个数为奇数时，中位数是这组数据中的一 个数据；但当数据个数为偶数时，其中位数是最中间两个数据的平均数，它不一定与这组数据中的某个数据相等．
例1 在一次中学生田径运动会上，参加男子跳高的17名运动员的成绩如下表所示：
成绩米
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的众数，中位数与平均数（计算结果保留到小数点后第2位）．
例2 10名工人某天生产同一零件，生产的件数是：
　15　17　14　10 15 19 17 16 14 12
　　求这一天10名工人生产的零件的中位数和众数．
平均数、中位数和众数有何特征：
平均数 中位数 众数
考虑所有的数据
便于使用
容易受极值的影响
是否惟一
解：把10个数据按大到小排列为：
19 17 17 16 15 15 14 14 12 10
所以这10名工人生产的零件的中位数为15，
众数为17，15，14．
知识网络：平均数、众数及中位数都是描述一组数据的集中趋势的特征数，但描述的角度和适用范围有所不同．
平均数的大小与一组数据里的每个数据均有关系，其中任何数据的变动都会相应引起平均数的变动；
众数着眼于对各数据出现的频数的考察，其大小只与这组数据中的部分数据有关．当一组数据中有不少数据多次重复出现时，其众数往往是我们关心的一种统计量；
中位数则仅与数据的排列位置有关，某些数据的变动对它的中位数没有影响．当一组数据中的个别数据变动较大时，可用它来描述其集中趋势．
3、该厂生产销售了一批女鞋３０双，其中各种尺码的销售量如下表所示：
鞋的尺（cm) 22 22.5 23 23.5 24 24.5 25
销售量（双） 1 2 5 11 7 3 1
1）.计算30双女鞋尺寸的平均数、中位数、众数
2）.从实际出发，请回答1中三种统计特征量
对指导本厂的生产是否有实际意义？
4、某班的教室里，三位同学正在为谁的数学成绩最好
而争论，他们的五次数学成绩分别是：
玲：62，94，95，98，98. 明：62，62，98，99，100.
丽：40，62，85，99，99.
他们都认为自己的成绩比另两位同学的好，请你结合
各组数据的三个数据代表，谈谈你的观点．
【本课小结】
1. 知识小结：这节课我们学习了众数、中位数的概念，了解了它们在描述一组数据集中趋势时的不同角度和适用范围．
2.方法小结：①众数由所给数据可直接求出，（一组数据中的众数可能不止一个，众数是一组数据中出现的次数最多的数据，而不是该数据出现的次数.如果有两个数据出现的次数相同，并且比其他数据出现次数都多，那么这两个数据都是这组数据的众数）．
②求中位数时，首先要先排序（从小到大或从大到小），然后计算中位数的序号，分数据为奇数个与偶数个两种来求.（既找出最中间的一个数据或最中间两个数并算出它们的平均数）．
补充练习1
1、已知一组数据10，10，x,8(由大到小排列)的中位数与平均数相等，求x值及这组数据的中位数．
解：∵10，10，x,8的中位数与平均数相等
∴ (10+x)/2＝ (10+10+x+8)/4 ∴x＝8,
(10+x)/2＝9 ∴这组数据中的中位数是9．
2、当5个整数从小到大排列，其中位数是4，如果这个数集的唯一众数是6，则这5个整数可能的最大的和是( )．
A.21 B.22 C.23 D.24．
A
分析：设这5个整数按从小到大排列为a1,a2,a3,a4,a5，由于中位数是4，所以a3＝4，又6是唯一众数，所以a4＝a5＝6，此时，a2最大只能取3，a1最大取2，故a1+a2+a3+a4+a5＝2+3+4+6+6＝21
1、2、3、3、4、5、6、7、7、8、
9、10 这12个数中，中位数是（ ），众数是（ ）
5、6的平均数为5.5
众数有两个：3和7
5.5
3和7
2000—2001赛季上海东方大鲨鱼篮球队队员身高的中位数、众数分别是多少？（书上217页）
答案：
中位数是： 1.97米；
众数是 ： 1.85米，1.96米，1.98米，2.02米
身高：
1.85、 1.85 、 1.86 、1.88 、 1.94
1.96 、 1.96 、 1.97 、 1.98 、 1.98
2.02 、 2.02 、 2.05 、 2.08 、 2.23