青岛版数学八年级下第8章平面图形的全等与相似复习提纲
文档属性
| 名称 | 青岛版数学八年级下第8章平面图形的全等与相似复习提纲 | 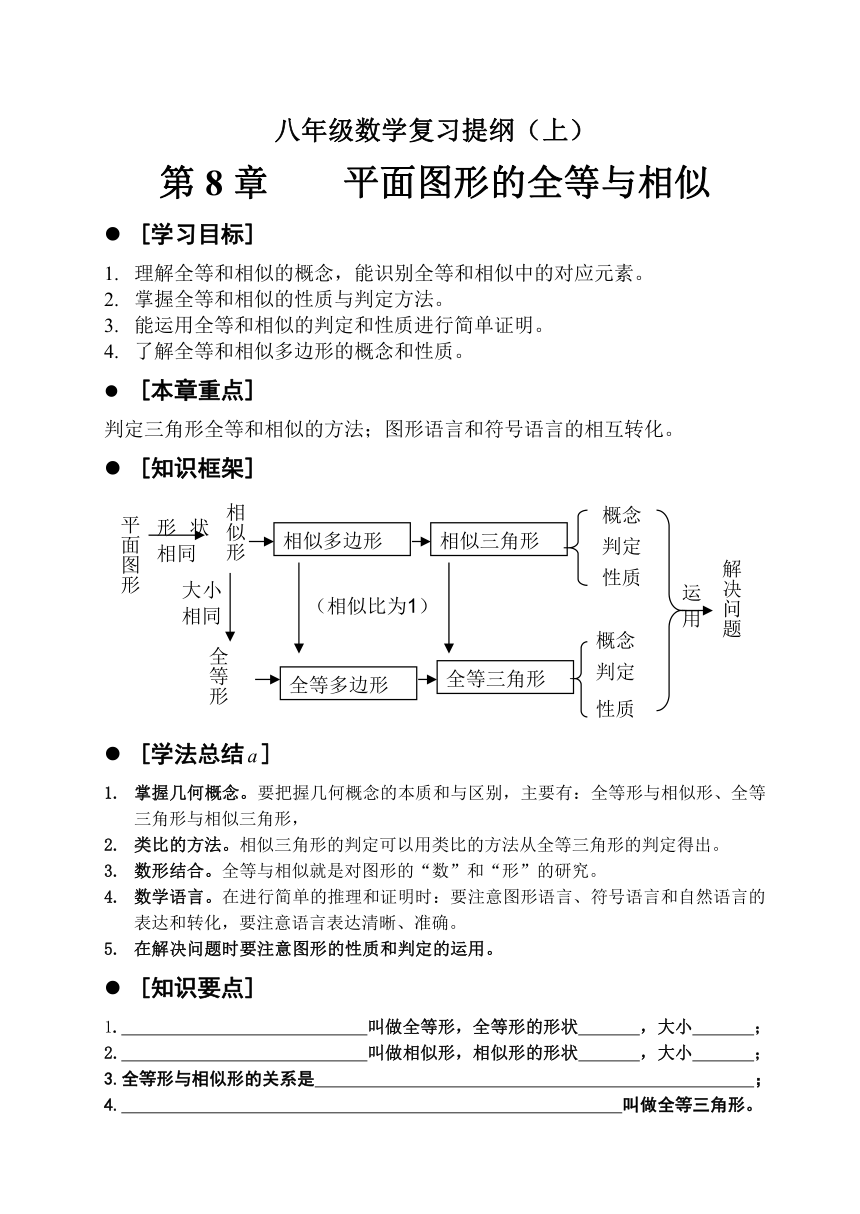 | |
| 格式 | zip | ||
| 文件大小 | 28.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-09 10:37:55 | ||
图片预览


文档简介
八年级数学复习提纲(上)
第8章 平面图形的全等与相似
[学习目标]
理解全等和相似的概念,能识别全等和相似中的对应元素。
掌握全等和相似的性质与判定方法。
能运用全等和相似的判定和性质进行简单证明。
了解全等和相似多边形的概念和性质。
[本章重点]
判定三角形全等和相似的方法;图形语言和符号语言的相互转化。
[知识框架]
[学法总结]
掌握几何概念。要把握几何概念的本质和与区别,主要有:全等形与相似形、全等三角形与相似三角形,
类比的方法。相似三角形的判定可以用类比的方法从全等三角形的判定得出。
数形结合。全等与相似就是对图形的“数”和“形”的研究。
数学语言。在进行简单的推理和证明时:要注意图形语言、符号语言和自然语言的表达和转化,要注意语言表达清晰、准确。
在解决问题时要注意图形的性质和判定的运用。
[知识要点]
1. 叫做全等形,全等形的形状 ,大小 ;
2. 叫做相似形,相似形的形状 ,大小 ;
3.全等形与相似形的关系是 ;
4. 叫做全等三角形。
5.全等三角形的性质:全等三角形的对应边 ,对应角 ,对应高 ,对应中线 ,对应角平分线 ;
6.全等三角形的判定方法有:
(1)ASA (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、
或 、 、
或 、 、 都能用ASA推出△ABC≌△DEF;
(2)AAS (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、 或 、 、 或 、 、 都能用ASA推出△ABC≌△DEF;
(3)SAS (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、 或 、 、 或 、 、 都能用ASA推出△ABC≌△DEF;
(4)SSS (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、 就能用ASA推出△ABC≌△DEF;
(5)HL(又叫做 ):用自然语言叙述为 ;
例如在图2中,要证明Rt△ABC≌Rt△DEF,
请写出下列条件的理论根据;
① AC=DF, BC=EF ( )
② AC=DF, AB=DE ( )
③ BC=EF, AB=DE ( )
④ ∠A=∠D,AC=DF ( )
⑤ ∠B=∠E,AB=DE( )
7. 叫做相似三角形;
8.相似三角形的性质:相似三角形的对应边 ,对应角 ,对应高的比 ,对应中线的比 ,对应角平分线的比 ;相似三角形对应周长的比 ,对应面积的比 ;
9.相似三角形的判定:
(1)方法一:
;
例如在图3中具备 、
或 、 ,
或 、 时可证明△ABC∽△DEF;
(2)方法二: ;
例如在图3中具备 、 或 、 ,或 、 时可证明△ABC∽△DEF;
(3)方法三: ;
例如在图3中具备 时可证明△ABC∽△DEF;
10. 叫做相似多边形。
11.相似多边形面积的比等于 。
[典型题目]
已知△DEF≌△MNP,且EF=NP,∠F=∠P,∠D=48°,∠E=52°,MN=12cm,求∠P的度数及DE的长。
如图4已知△ABC和△AED是等边三角形,求证:BE=CD。
3.如图5,已知AB=AC,DB=DC,F是AD延长线上的任意一点,
求证:△ABF≌△ACF.
4.如图6,△BEA∽△BAD,写出图中所有相等的角和成比例线段的比例式。
5.如图7,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为48,
求△ADE的面积。
6.如图8,有一块三角形木块ABC,要从上面裁出一个矩形PQMN,使这个矩形的长是宽的2倍,已知BC=60cm,高AD=45cm,求矩形的长和宽。
7.一个五边形的各边的长分别是1,2,3,4,5,和它相似的另一个五边形的最大边的长为7,后一个五边形的其他各边的长分别是多少?
8.如图9,已知AB=AC,AD=AE,求证:BD=EC。
9.如图10,△ABC中,AB>AC,过AC上一点D作直线DE交AB于点E,得△ADE,要使所得的三角形与原三角形相似,这样的直线可作多少条?
性质
平面图形
相似形
形状相同
全等形
大小相同
概念
判定
性质
全等三角形
相似三角形
相似多边形
概念
判定
全等多边形
(相似比为1)
解决问题
运用
第8章 平面图形的全等与相似
[学习目标]
理解全等和相似的概念,能识别全等和相似中的对应元素。
掌握全等和相似的性质与判定方法。
能运用全等和相似的判定和性质进行简单证明。
了解全等和相似多边形的概念和性质。
[本章重点]
判定三角形全等和相似的方法;图形语言和符号语言的相互转化。
[知识框架]
[学法总结]
掌握几何概念。要把握几何概念的本质和与区别,主要有:全等形与相似形、全等三角形与相似三角形,
类比的方法。相似三角形的判定可以用类比的方法从全等三角形的判定得出。
数形结合。全等与相似就是对图形的“数”和“形”的研究。
数学语言。在进行简单的推理和证明时:要注意图形语言、符号语言和自然语言的表达和转化,要注意语言表达清晰、准确。
在解决问题时要注意图形的性质和判定的运用。
[知识要点]
1. 叫做全等形,全等形的形状 ,大小 ;
2. 叫做相似形,相似形的形状 ,大小 ;
3.全等形与相似形的关系是 ;
4. 叫做全等三角形。
5.全等三角形的性质:全等三角形的对应边 ,对应角 ,对应高 ,对应中线 ,对应角平分线 ;
6.全等三角形的判定方法有:
(1)ASA (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、
或 、 、
或 、 、 都能用ASA推出△ABC≌△DEF;
(2)AAS (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、 或 、 、 或 、 、 都能用ASA推出△ABC≌△DEF;
(3)SAS (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、 或 、 、 或 、 、 都能用ASA推出△ABC≌△DEF;
(4)SSS (又叫做 ):用自然语言叙述为 ;
例如在图1中,应满足 、 、 就能用ASA推出△ABC≌△DEF;
(5)HL(又叫做 ):用自然语言叙述为 ;
例如在图2中,要证明Rt△ABC≌Rt△DEF,
请写出下列条件的理论根据;
① AC=DF, BC=EF ( )
② AC=DF, AB=DE ( )
③ BC=EF, AB=DE ( )
④ ∠A=∠D,AC=DF ( )
⑤ ∠B=∠E,AB=DE( )
7. 叫做相似三角形;
8.相似三角形的性质:相似三角形的对应边 ,对应角 ,对应高的比 ,对应中线的比 ,对应角平分线的比 ;相似三角形对应周长的比 ,对应面积的比 ;
9.相似三角形的判定:
(1)方法一:
;
例如在图3中具备 、
或 、 ,
或 、 时可证明△ABC∽△DEF;
(2)方法二: ;
例如在图3中具备 、 或 、 ,或 、 时可证明△ABC∽△DEF;
(3)方法三: ;
例如在图3中具备 时可证明△ABC∽△DEF;
10. 叫做相似多边形。
11.相似多边形面积的比等于 。
[典型题目]
已知△DEF≌△MNP,且EF=NP,∠F=∠P,∠D=48°,∠E=52°,MN=12cm,求∠P的度数及DE的长。
如图4已知△ABC和△AED是等边三角形,求证:BE=CD。
3.如图5,已知AB=AC,DB=DC,F是AD延长线上的任意一点,
求证:△ABF≌△ACF.
4.如图6,△BEA∽△BAD,写出图中所有相等的角和成比例线段的比例式。
5.如图7,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为48,
求△ADE的面积。
6.如图8,有一块三角形木块ABC,要从上面裁出一个矩形PQMN,使这个矩形的长是宽的2倍,已知BC=60cm,高AD=45cm,求矩形的长和宽。
7.一个五边形的各边的长分别是1,2,3,4,5,和它相似的另一个五边形的最大边的长为7,后一个五边形的其他各边的长分别是多少?
8.如图9,已知AB=AC,AD=AE,求证:BD=EC。
9.如图10,△ABC中,AB>AC,过AC上一点D作直线DE交AB于点E,得△ADE,要使所得的三角形与原三角形相似,这样的直线可作多少条?
性质
平面图形
相似形
形状相同
全等形
大小相同
概念
判定
性质
全等三角形
相似三角形
相似多边形
概念
判定
全等多边形
(相似比为1)
解决问题
运用
同课章节目录
