青岛版数学八年级下第9章解直角三角形复习提纲
文档属性
| 名称 | 青岛版数学八年级下第9章解直角三角形复习提纲 |  | |
| 格式 | zip | ||
| 文件大小 | 390.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-09 10:43:54 | ||
图片预览

文档简介
八年级数学复习提纲(上)
第9章 解直角三角形
[学习目标]
利用相似三角形探索锐角三角比,知道30°、45°、60°角的三角比。
会利用计算器求已知锐角的三角比,由已知的三角比求它的对应锐角。
能用锐角三角比解直角三角形,并能用相关知识解决简单的实际问题。
[本章重点] 锐角三角比的概念及解直角三角形的基本类型和方法 。
[知识框架]
[学法总结]
正确理解数学概念:锐角三角比(正弦、余弦、正切)的本质是两条线段的比,它们只是一个数值没有单位。其大小只与角的大小有关,与所在的三角形无关,与角的两边的长度无关。
掌握规律轻松记忆:要记住特殊角(30°、45°、60°)的锐角三角比。
学会运用数学语言:图形语言、符号语言和自然语言的相互转化和运用。若题目中没有图形,应先画出图形,然后结合图形、根据题目中的已知条件选择合适的关系式求解。
掌握“化斜为直”方法:对于非直角三角形的问题,通常利用作辅助线把它转化为直角三角形。并注意利用率特殊角来构造直角三角形。
解决实际问题时,正确审题,弄清题意是前提,找到(或构造)与问题有关的直角三角形是关键。选择合适的边角关系利用方程的思想方法去求值是常用的方法。对于结果要按题目的要求保留准确值或近似值。
[知识要点]
锐角三角比:
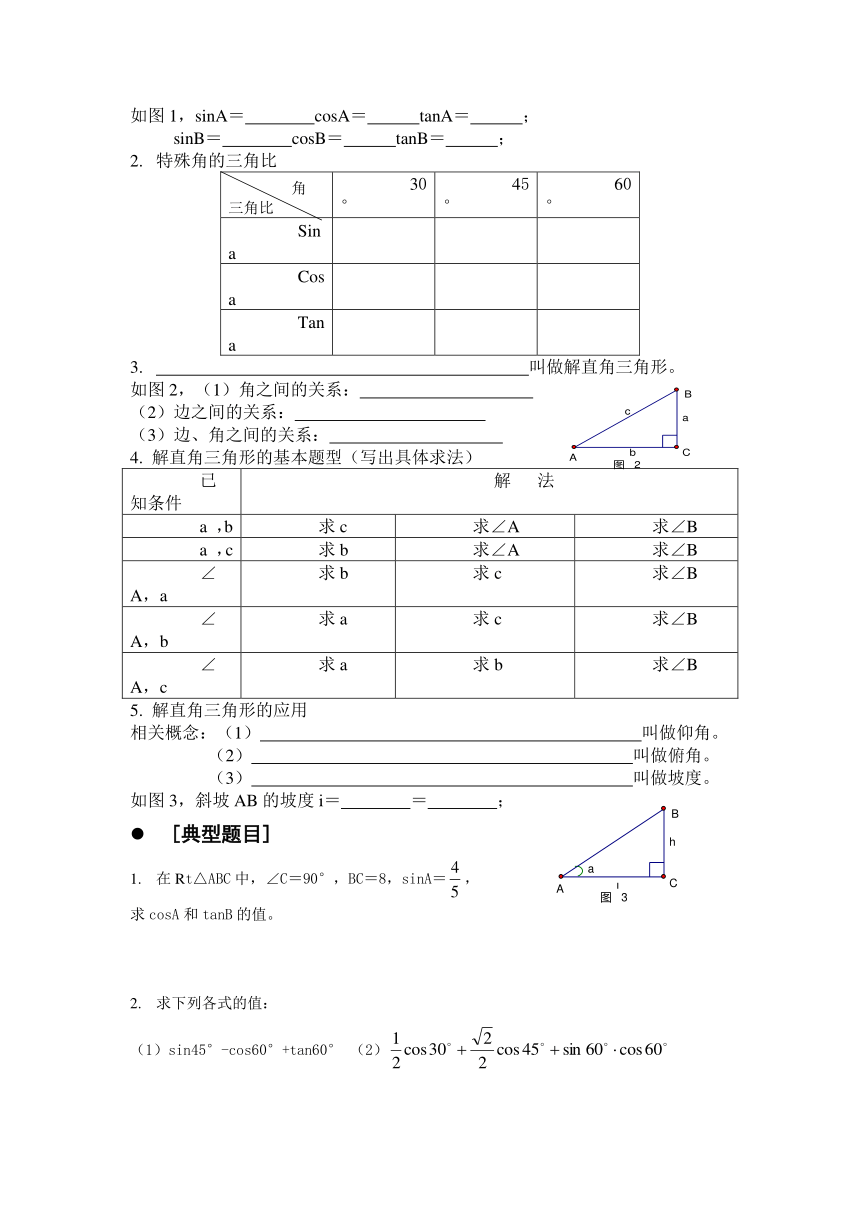
如图1,sinA= cosA= tanA= ;
sinB= cosB= tanB= ;
特殊角的三角比
三角比 30° 45° 60°
Sin a
Cos a
Tan a
叫做解直角三角形。
如图2,(1)角之间的关系:
(2)边之间的关系:
(3)边、角之间的关系:
4. 解直角三角形的基本题型(写出具体求法)
已知条件 解 法
a ,b 求c 求∠A 求∠B
a ,c 求b 求∠A 求∠B
∠A,a 求b 求c 求∠B
∠A,b 求a 求c 求∠B
∠A,c 求a 求b 求∠B
5. 解直角三角形的应用
相关概念:(1) 叫做仰角。
(2) 叫做俯角。
(3) 叫做坡度。
如图3,斜坡AB的坡度i= = ;
[典型题目]
在Rt△ABC中,∠C=90°,BC=8,sinA=,
求cosA和tanB的值。
求下列各式的值:
(1)sin45°-cos60°+tan60° (2)
(3)(4)sin230°-cos230°-tan45°
3. 在Rt△ABC中,∠C=90°,根据下列条件,解直角三角形:
(1)AC=,BC=
(2)AB=15,∠B=60°
4.在旧城改造中,要拆除一座烟囱AB,(如图4),在地面上事先划定以B为加以,半径与AB等长的圆形危险区,现在从离B点21米远的楼CD的顶端C点测得A点的仰角为45°,B点的俯角为30°,离B点35米远处的一处保护文物是否在危险区内?
5. 如图5一段河堤的斜坡BC=12米,为了加固河堤,需要将堤坝加厚,竣工后,斜坡的坡度由原来的1:2变为1:3,加固后斜坡AD的长是多少米?
6. 有一块如图所示的四边形空地,求此空地的面积(结果精确到0.01m2).
7. 如图,甲,乙两楼相距30m,甲楼高40m,自甲楼楼顶看乙楼楼顶,仰角为300乙楼有多高 (结果精确到1m).
8. 如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为600,爬到楼顶D处测得塔顶的仰角为300,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m).
锐角三角比
锐角三角比的定义
特殊角的锐角三角比
用计算器求锐角三角比
解直角三角形
直角三角形的边角关系
两种类型
已知一边和一锐角
已知两边
已知斜边和一锐角
已知一直角边和一锐角
已知两条直角边
已知斜边和一直角边
解直角三角形的应用
锐角三角比的求法
角的关系:三角形的内角和
边的关系:勾股定理
边角关系:锐角三角比
正弦、余弦、正切
角
20m
30m
50m
50m
600
600
第9章 解直角三角形
[学习目标]
利用相似三角形探索锐角三角比,知道30°、45°、60°角的三角比。
会利用计算器求已知锐角的三角比,由已知的三角比求它的对应锐角。
能用锐角三角比解直角三角形,并能用相关知识解决简单的实际问题。
[本章重点] 锐角三角比的概念及解直角三角形的基本类型和方法 。
[知识框架]
[学法总结]
正确理解数学概念:锐角三角比(正弦、余弦、正切)的本质是两条线段的比,它们只是一个数值没有单位。其大小只与角的大小有关,与所在的三角形无关,与角的两边的长度无关。
掌握规律轻松记忆:要记住特殊角(30°、45°、60°)的锐角三角比。
学会运用数学语言:图形语言、符号语言和自然语言的相互转化和运用。若题目中没有图形,应先画出图形,然后结合图形、根据题目中的已知条件选择合适的关系式求解。
掌握“化斜为直”方法:对于非直角三角形的问题,通常利用作辅助线把它转化为直角三角形。并注意利用率特殊角来构造直角三角形。
解决实际问题时,正确审题,弄清题意是前提,找到(或构造)与问题有关的直角三角形是关键。选择合适的边角关系利用方程的思想方法去求值是常用的方法。对于结果要按题目的要求保留准确值或近似值。
[知识要点]
锐角三角比:
如图1,sinA= cosA= tanA= ;
sinB= cosB= tanB= ;
特殊角的三角比
三角比 30° 45° 60°
Sin a
Cos a
Tan a
叫做解直角三角形。
如图2,(1)角之间的关系:
(2)边之间的关系:
(3)边、角之间的关系:
4. 解直角三角形的基本题型(写出具体求法)
已知条件 解 法
a ,b 求c 求∠A 求∠B
a ,c 求b 求∠A 求∠B
∠A,a 求b 求c 求∠B
∠A,b 求a 求c 求∠B
∠A,c 求a 求b 求∠B
5. 解直角三角形的应用
相关概念:(1) 叫做仰角。
(2) 叫做俯角。
(3) 叫做坡度。
如图3,斜坡AB的坡度i= = ;
[典型题目]
在Rt△ABC中,∠C=90°,BC=8,sinA=,
求cosA和tanB的值。
求下列各式的值:
(1)sin45°-cos60°+tan60° (2)
(3)(4)sin230°-cos230°-tan45°
3. 在Rt△ABC中,∠C=90°,根据下列条件,解直角三角形:
(1)AC=,BC=
(2)AB=15,∠B=60°
4.在旧城改造中,要拆除一座烟囱AB,(如图4),在地面上事先划定以B为加以,半径与AB等长的圆形危险区,现在从离B点21米远的楼CD的顶端C点测得A点的仰角为45°,B点的俯角为30°,离B点35米远处的一处保护文物是否在危险区内?
5. 如图5一段河堤的斜坡BC=12米,为了加固河堤,需要将堤坝加厚,竣工后,斜坡的坡度由原来的1:2变为1:3,加固后斜坡AD的长是多少米?
6. 有一块如图所示的四边形空地,求此空地的面积(结果精确到0.01m2).
7. 如图,甲,乙两楼相距30m,甲楼高40m,自甲楼楼顶看乙楼楼顶,仰角为300乙楼有多高 (结果精确到1m).
8. 如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为600,爬到楼顶D处测得塔顶的仰角为300,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m).
锐角三角比
锐角三角比的定义
特殊角的锐角三角比
用计算器求锐角三角比
解直角三角形
直角三角形的边角关系
两种类型
已知一边和一锐角
已知两边
已知斜边和一锐角
已知一直角边和一锐角
已知两条直角边
已知斜边和一直角边
解直角三角形的应用
锐角三角比的求法
角的关系:三角形的内角和
边的关系:勾股定理
边角关系:锐角三角比
正弦、余弦、正切
角
20m
30m
50m
50m
600
600
同课章节目录
