沪教版(上海)数学八年级第二学期-20章小结 《一次函数背景下的面积问题》复习课 教案
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-20章小结 《一次函数背景下的面积问题》复习课 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 21:56:40 | ||
图片预览

文档简介
《一次函数背景下的面积问题》复习课
授课时间:
授课班级:
授课教师:
教学目标:
1、巩固一次函数的图象与性质,能利用解析式求图形的面积.
2、通过对已知图形面积求值的探究,理解一次函数图象特征与解析式的联系规律,体会数形结合思想,化归思想和方程思想.
教学重点
重点:根据函数解析式求三角形或四边形的面积.
教学难点
难点:不规则图形面积的计算
教学过程设计
一、课前预习交流
1、一次函数与x轴的交点A的坐标是
与y轴的交点B的坐标是
________.
2、直线与直线的交点坐标是______________.
3、已知点A(2,0)、B(6,0),求线段AB=___________.
4、已知点A(6,4)、B(6,-2),求线段AB=___________.
5、已知点A(3,4)、B(6,0),求线段AB=___________.
6、已知直线AB:,求此一次函数的图象与两坐标轴所围成的三角形的面积.
【求一条直线与两坐标轴所围成三角形面积(规则图形
--公式法)】
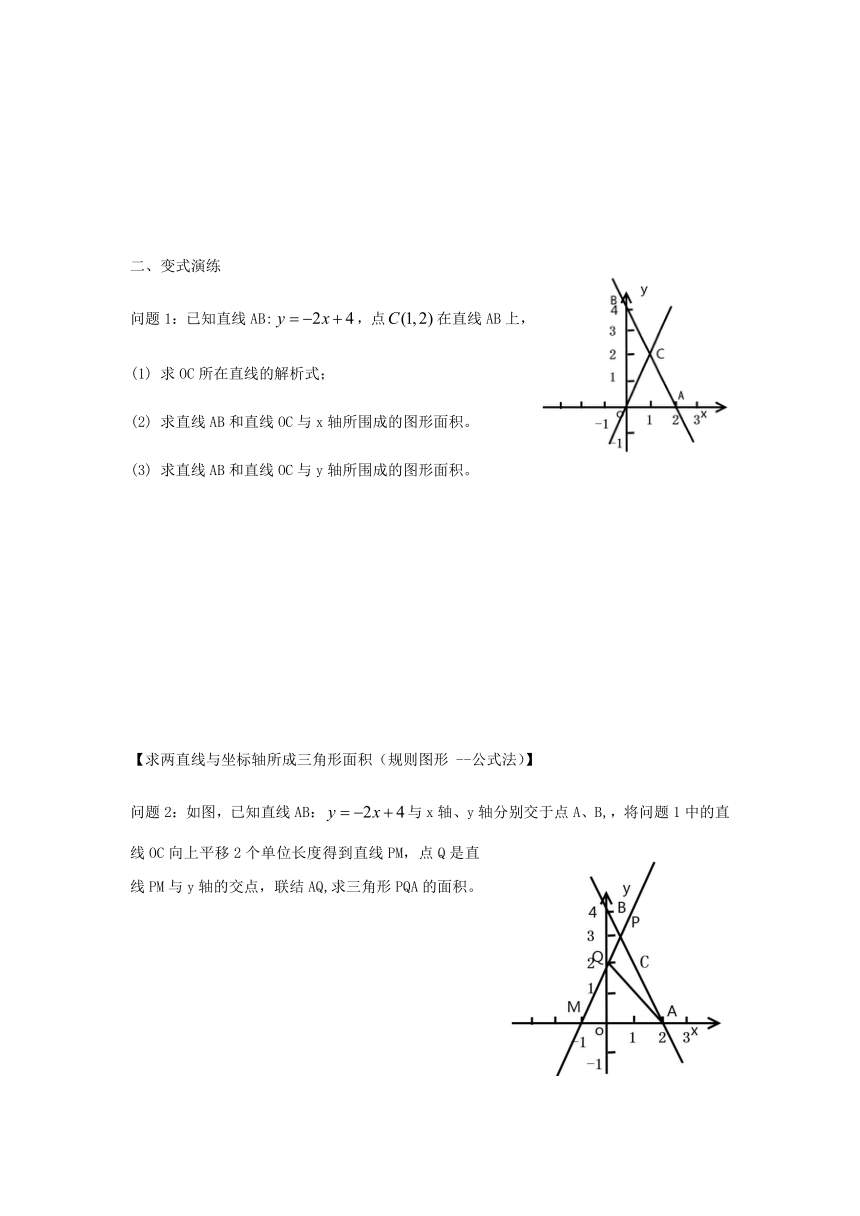
二、变式演练
问题1:已知直线AB:,点在直线AB上,
(1)
求OC所在直线的解析式;
(2)
求直线AB和直线OC与x轴所围成的图形面积。
(3)
求直线AB和直线OC与y轴所围成的图形面积。
【求两直线与坐标轴所成三角形面积(规则图形
--公式法)】
问题2:如图,已知直线AB:与x轴、y轴分别交于点A、B,,将问题1中的直线OC向上平移2个单位长度得到直线PM,点Q是直线PM与y轴的交点,联结AQ,求三角形PQA的面积。
【求点p坐标,需要联立两直线的解析式,求解方程组;求三边都不平行于坐标轴的三角形面积(割补法)】
三、巩固提升
1、如图所示:直线经过点B(0,2)与点C(-1,3),且与x轴交与点A,经过点E(-4,0)的直线与OC:y=-3x平行,并且与直线交与点D,
(1)求BC所在直线的函数解析式
(2)求点D的坐标;
(3)求四边形CDEO的面积
四、课堂小结
1、已知解析式求面积
(1)如果三角形有一边在坐标轴上(或平行于坐标轴),直接用面积公式求面积.
(2)如果三角形任何一边都不在坐标轴上,也不平行于坐标轴,则需分割为几个有边在坐标轴上的三角形面积之和(或差).
(3)不规则四边形面积常转化为若干个三角形面积或特殊四边形面积之和(或差).
授课时间:
授课班级:
授课教师:
教学目标:
1、巩固一次函数的图象与性质,能利用解析式求图形的面积.
2、通过对已知图形面积求值的探究,理解一次函数图象特征与解析式的联系规律,体会数形结合思想,化归思想和方程思想.
教学重点
重点:根据函数解析式求三角形或四边形的面积.
教学难点
难点:不规则图形面积的计算
教学过程设计
一、课前预习交流
1、一次函数与x轴的交点A的坐标是
与y轴的交点B的坐标是
________.
2、直线与直线的交点坐标是______________.
3、已知点A(2,0)、B(6,0),求线段AB=___________.
4、已知点A(6,4)、B(6,-2),求线段AB=___________.
5、已知点A(3,4)、B(6,0),求线段AB=___________.
6、已知直线AB:,求此一次函数的图象与两坐标轴所围成的三角形的面积.
【求一条直线与两坐标轴所围成三角形面积(规则图形
--公式法)】
二、变式演练
问题1:已知直线AB:,点在直线AB上,
(1)
求OC所在直线的解析式;
(2)
求直线AB和直线OC与x轴所围成的图形面积。
(3)
求直线AB和直线OC与y轴所围成的图形面积。
【求两直线与坐标轴所成三角形面积(规则图形
--公式法)】
问题2:如图,已知直线AB:与x轴、y轴分别交于点A、B,,将问题1中的直线OC向上平移2个单位长度得到直线PM,点Q是直线PM与y轴的交点,联结AQ,求三角形PQA的面积。
【求点p坐标,需要联立两直线的解析式,求解方程组;求三边都不平行于坐标轴的三角形面积(割补法)】
三、巩固提升
1、如图所示:直线经过点B(0,2)与点C(-1,3),且与x轴交与点A,经过点E(-4,0)的直线与OC:y=-3x平行,并且与直线交与点D,
(1)求BC所在直线的函数解析式
(2)求点D的坐标;
(3)求四边形CDEO的面积
四、课堂小结
1、已知解析式求面积
(1)如果三角形有一边在坐标轴上(或平行于坐标轴),直接用面积公式求面积.
(2)如果三角形任何一边都不在坐标轴上,也不平行于坐标轴,则需分割为几个有边在坐标轴上的三角形面积之和(或差).
(3)不规则四边形面积常转化为若干个三角形面积或特殊四边形面积之和(或差).
