沪教版(上海)数学七年级第二学期-14.2 三角形的内角和(1) 教案
文档属性
| 名称 | 沪教版(上海)数学七年级第二学期-14.2 三角形的内角和(1) 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 31.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 21:42:28 | ||
图片预览


文档简介
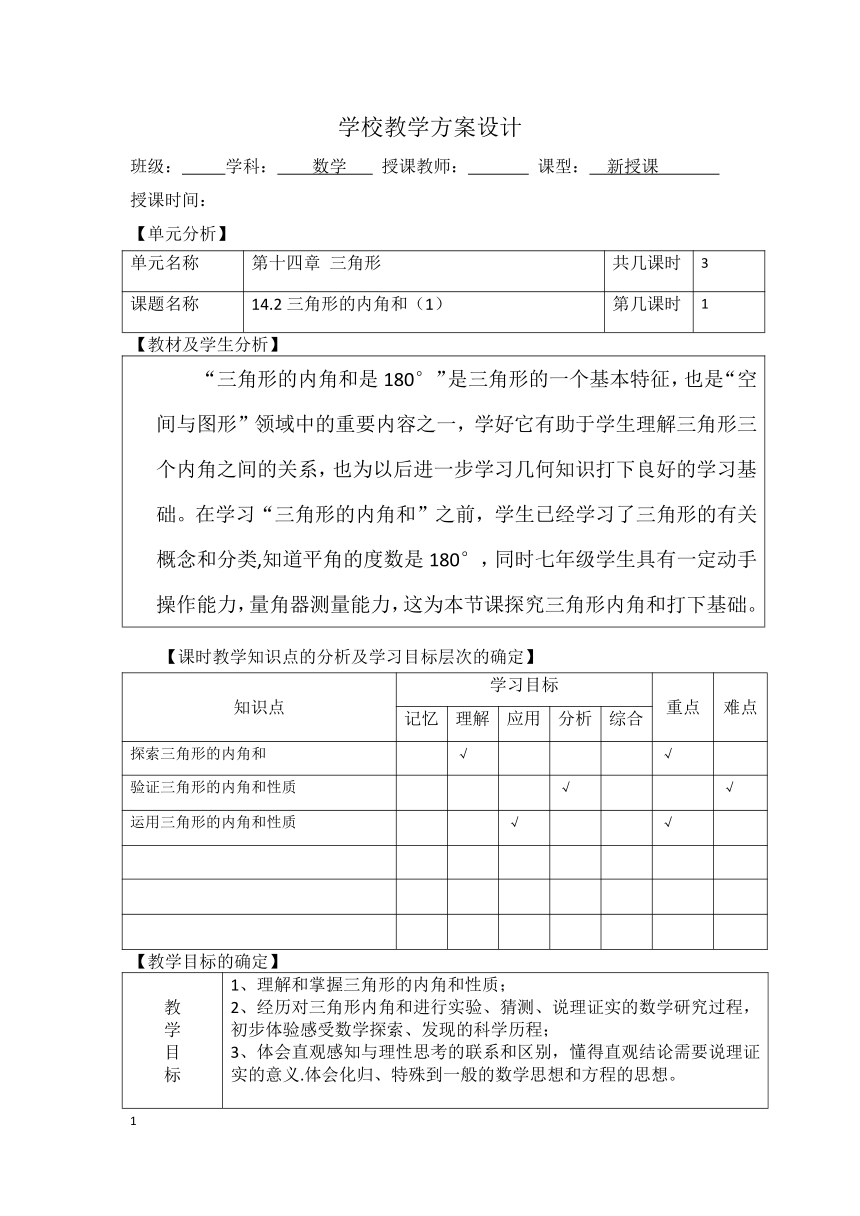
学校教学方案设计
班级:
学科:
数学
授课教师:
课型:
新授课
授课时间:
【单元分析】
单元名称
第十四章
三角形
共几课时
3
课题名称
14.2三角形的内角和(1)
第几课时
1
【教材及学生分析】
“三角形的内角和是180°”是三角形的一个基本特征,也是“空间与图形”领域中的重要内容之一,学好它有助于学生理解三角形三个内角之间的关系,也为以后进一步学习几何知识打下良好的学习基础。在学习“三角形的内角和”之前,学生已经学习了三角形的有关概念和分类,知道平角的度数是180°,同时七年级学生具有一定动手操作能力,量角器测量能力,这为本节课探究三角形内角和打下基础。
【课时教学知识点的分析及学习目标层次的确定】
知识点
学习目标
重点
难点
记忆
理解
应用
分析
综合
探索三角形的内角和
√
√
验证三角形的内角和性质
√
√
运用三角形的内角和性质
√
√
【教学目标的确定】
教
学
目
标
1、理解和掌握三角形的内角和性质;
2、经历对三角形内角和进行实验、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程;
3、体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义.体会化归、特殊到一般的数学思想和方程的思想。
【教学重点和难点】
项目
内容
解决措施
重点
三角形的内角和性质的推导,会用这一性质进行说理、计算和判断
通过几个常见特殊的三角形内角求和
到探索一般三角形的内角和,循序渐进,让学生动手操作与说理证明相结合理解、掌握三角形内角和性质。
难点
探索、归纳并证实三角形的内角和性质。
【教学方法与手段】
教学方法
引导发现法、实验探究法
【教学过程设计】
教学
步骤
教师活动
学生活动
教学意图
时间
分配
教
学
过
程
课前准备:
课件、教具、学习单
预习,准备好三角形纸片,量角器
熟悉内容
导入:
一、复习引入
1.复习旧知识,三角形的三边有什么关系?
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边
2.引出要探究的内容:那么三角形的三个角有什么关系?
3.三角形内角兄弟之争的小故事
生:举手回答
生:阅读思考
复习三角形的基本概念
引发学生兴趣,探究其中的道理,给出课题:14.2三角形的内角和(1)。
5
新课:
猜想
老师展示一副三角尺和等边三角形,请学生分别讲出三角形各角的度数,并求出三个内角的和.
猜想一下任意一个三角形三个角之间关系:三角形的内角和等于180°.
验证
请同学们拿出准备好的任意三角形纸片,问如何验证三角形的内角和等于180°?.
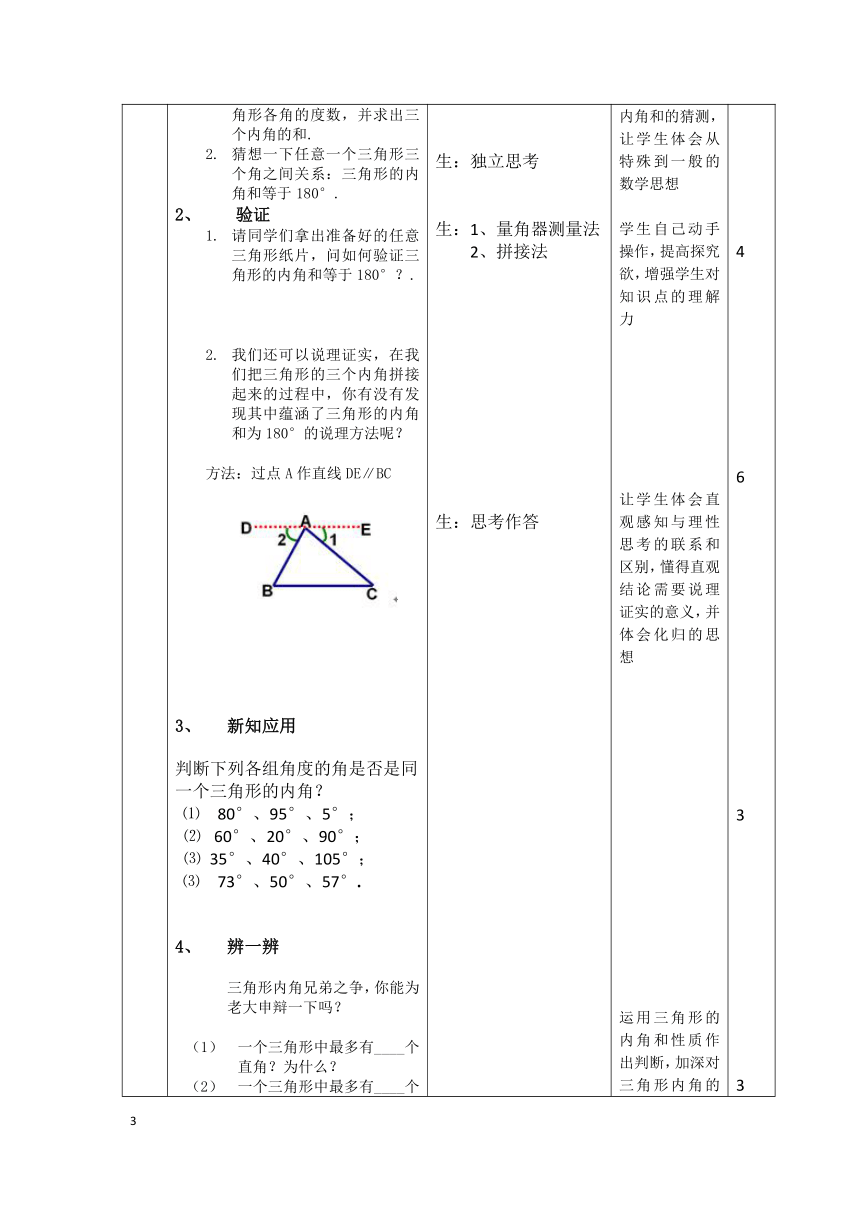
我们还可以说理证实,在我们把三角形的三个内角拼接起来的过程中,你有没有发现其中蕴涵了三角形的内角和为180°的说理方法呢?
方法:过点A作直线DE∥BC
新知应用
判断下列各组角度的角是否是同一个三角形的内角?
80°、95°、5°;
60°、20°、90°;
⑶
35°、40°、105°;
73°、50°、57°.
辨一辨
三角形内角兄弟之争,你能为老大申辩一下吗?
一个三角形中最多有____个直角?为什么?
一个三角形中最多有____个钝角?为什么?
一个三角形中至少有____个锐角?为什么?
例题讲解
例1、在△ABC中,已知∠B=35°,∠C=55°,求∠A的度数,并判断△ABC的类型
练习1:P80,
2
例2、在△ABC中,已知∠A:∠B:∠C=1:2:3,求∠A、∠B、∠C的度数
练习2:P80,
4
拓展练习
在⊿ABC中,已知角平分线BF、CE相交于点O,
(1)如∠A=50°,求∠BOC的度数
(2)如果∠A=n°,求∠BOC的度数
生:看尺作答
生:独立思考
生:1、量角器测量法
2、拼接法
生:思考作答
生:举手口答
生:动笔计算
生:独立思考
举手作答
从特殊三角形内角和的计算到一般三角形内角和的猜测,让学生体会从特殊到一般的数学思想
学生自己动手操作,提高探究欲,增强学生对知识点的理解力
让学生体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义,并体会化归的思想
运用三角形的内角和性质作出判断,加深对三角形内角的认识
直接运用三角形的内角和性质及三角形的分类进行计算判断
例2体现了方程思想在几何说理中的应用,要根据已知条件先设元,再根据三角形的内角和性质建立方程求解
能力提升题考察的是三角形内角和及角平分线知识的综合应用,由易到难,层层递进,逐步激发学生的探索兴趣和求知欲
2
4
6
3
3
4
3
4
4
课堂
小结
说一说,这节课你学到了什么?
还感受到了什么?
(1)三角形的内角和性质;
(2)通过今天的学习,在前面第13章的基础上我们又多了一种求角的方法;
(3)体会化归、从特殊到一般的数学思想和方程的思想。
2
布置
作业
练习册:14.2(1)
课课练:14.2(1)
板书
设计
14.2(1)三角形的内角和
概念
1.三角形的内角和为
2.一个三角形中最多有____个锐角,
一个三角形中最多有____个直角,
一个三角形中最多有____个钝角
课后
反思
《三角形的内角和》教学反思
今天我讲了《三角形的内角和》一课,课前我分析:学生已经掌握了三角形的概念、分类,熟悉了钝角、锐角、平角这些角的知识。对于三角形的内角和是多少度,学生是不陌生的,因为学生有以前认识角、用量角器量三角板三个角的度数以及三角形的分类的基础,很多孩子都能回答出三角形的内角和是180度,但是他们却不知道怎样才能得出三角形的内角和是180度。
根据学情我设置了以下教学目标:
1、理解和掌握三角形的内角和性质;
2、经历对三角形内角和进行实验、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程;
3、体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义.体会化归、特殊到一般的数学思想和方程的思想。
在探究三角形的内角和时,我遵循由特殊到一般的认知规律,从学生熟悉的三角板入手抽象出特殊的三角形,计算出每块三角板的内角和是180°,接下来很自然地引导学生猜想:是不是所有的三角形的内角和都是180
°给学生提供一些材料,引导他们去探究出结论。学生任意画一个三角形进行验证,让学生经历从特殊到普遍的过程。这是动手操作的过程。因为前面没有试教过,所以在这里花的时间比较多,我自己觉得课上得有点拖,也有点沉闷。但在这一过程中,我也发现了很多的问题。很多学生是运用180度这个结论来量的。比如说他先量了二个角,最后一个角就不量了,直接用180度减去前面二个角,就是第三个角;还有很多同学,我让裁的是任意三角形,他们图方便全裁的直角三角形。我想如果这样的话就失去了测量的意义了。在交流的过程中,很多同学都说他们测量的结果是180度,导致另外一些不是180度的学生不敢表达自己的意见。我想面对这样的问题,如果我在交流反馈的时候,再多加一个环节,问你量出来的三个角分别是几度,内角和是几度,这样是不是会减少一些这样的问题。第二种方法是剪剪拼拼,我高估了学生的动手能力,几乎没有学生想到这种方法,其实可以直接告诉学生,剪下三个角来拼一拼,看看有什么发现。通过了解,其实有一些学生是知道的。如果我选用抛问题的方法,可能会出现一些亮点。下面在说理证明三角形内角和为180时,我提示学生添加辅助线平行线的方法,这样做让学生缺少了思考的机会,其实可以把整节课的大部分时间放在说理证明三角形内角和上,让学生们独立思考证明的方法,或许这样学生的参与度会更高,课堂氛围也能活跃起来。
整堂课下来,我自己觉得上得很沉闷,学生的注意力也不是非常集中,当然这和我自己有很大的关系,课堂气氛没能调节得很好。在自己的课中,我就觉得虽然验证的过程很严密,从特殊到普遍这样一个过程,但是留给学生思考的空间特别少,学生只是进行一些操作。总而言之,在上课的过程中,给了我一次学习的过程,在教案设计时,该怎么样把每一个环节落实到位,怎么样说好每一句话,预设好每一个环节。
1
班级:
学科:
数学
授课教师:
课型:
新授课
授课时间:
【单元分析】
单元名称
第十四章
三角形
共几课时
3
课题名称
14.2三角形的内角和(1)
第几课时
1
【教材及学生分析】
“三角形的内角和是180°”是三角形的一个基本特征,也是“空间与图形”领域中的重要内容之一,学好它有助于学生理解三角形三个内角之间的关系,也为以后进一步学习几何知识打下良好的学习基础。在学习“三角形的内角和”之前,学生已经学习了三角形的有关概念和分类,知道平角的度数是180°,同时七年级学生具有一定动手操作能力,量角器测量能力,这为本节课探究三角形内角和打下基础。
【课时教学知识点的分析及学习目标层次的确定】
知识点
学习目标
重点
难点
记忆
理解
应用
分析
综合
探索三角形的内角和
√
√
验证三角形的内角和性质
√
√
运用三角形的内角和性质
√
√
【教学目标的确定】
教
学
目
标
1、理解和掌握三角形的内角和性质;
2、经历对三角形内角和进行实验、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程;
3、体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义.体会化归、特殊到一般的数学思想和方程的思想。
【教学重点和难点】
项目
内容
解决措施
重点
三角形的内角和性质的推导,会用这一性质进行说理、计算和判断
通过几个常见特殊的三角形内角求和
到探索一般三角形的内角和,循序渐进,让学生动手操作与说理证明相结合理解、掌握三角形内角和性质。
难点
探索、归纳并证实三角形的内角和性质。
【教学方法与手段】
教学方法
引导发现法、实验探究法
【教学过程设计】
教学
步骤
教师活动
学生活动
教学意图
时间
分配
教
学
过
程
课前准备:
课件、教具、学习单
预习,准备好三角形纸片,量角器
熟悉内容
导入:
一、复习引入
1.复习旧知识,三角形的三边有什么关系?
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边
2.引出要探究的内容:那么三角形的三个角有什么关系?
3.三角形内角兄弟之争的小故事
生:举手回答
生:阅读思考
复习三角形的基本概念
引发学生兴趣,探究其中的道理,给出课题:14.2三角形的内角和(1)。
5
新课:
猜想
老师展示一副三角尺和等边三角形,请学生分别讲出三角形各角的度数,并求出三个内角的和.
猜想一下任意一个三角形三个角之间关系:三角形的内角和等于180°.
验证
请同学们拿出准备好的任意三角形纸片,问如何验证三角形的内角和等于180°?.
我们还可以说理证实,在我们把三角形的三个内角拼接起来的过程中,你有没有发现其中蕴涵了三角形的内角和为180°的说理方法呢?
方法:过点A作直线DE∥BC
新知应用
判断下列各组角度的角是否是同一个三角形的内角?
80°、95°、5°;
60°、20°、90°;
⑶
35°、40°、105°;
73°、50°、57°.
辨一辨
三角形内角兄弟之争,你能为老大申辩一下吗?
一个三角形中最多有____个直角?为什么?
一个三角形中最多有____个钝角?为什么?
一个三角形中至少有____个锐角?为什么?
例题讲解
例1、在△ABC中,已知∠B=35°,∠C=55°,求∠A的度数,并判断△ABC的类型
练习1:P80,
2
例2、在△ABC中,已知∠A:∠B:∠C=1:2:3,求∠A、∠B、∠C的度数
练习2:P80,
4
拓展练习
在⊿ABC中,已知角平分线BF、CE相交于点O,
(1)如∠A=50°,求∠BOC的度数
(2)如果∠A=n°,求∠BOC的度数
生:看尺作答
生:独立思考
生:1、量角器测量法
2、拼接法
生:思考作答
生:举手口答
生:动笔计算
生:独立思考
举手作答
从特殊三角形内角和的计算到一般三角形内角和的猜测,让学生体会从特殊到一般的数学思想
学生自己动手操作,提高探究欲,增强学生对知识点的理解力
让学生体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义,并体会化归的思想
运用三角形的内角和性质作出判断,加深对三角形内角的认识
直接运用三角形的内角和性质及三角形的分类进行计算判断
例2体现了方程思想在几何说理中的应用,要根据已知条件先设元,再根据三角形的内角和性质建立方程求解
能力提升题考察的是三角形内角和及角平分线知识的综合应用,由易到难,层层递进,逐步激发学生的探索兴趣和求知欲
2
4
6
3
3
4
3
4
4
课堂
小结
说一说,这节课你学到了什么?
还感受到了什么?
(1)三角形的内角和性质;
(2)通过今天的学习,在前面第13章的基础上我们又多了一种求角的方法;
(3)体会化归、从特殊到一般的数学思想和方程的思想。
2
布置
作业
练习册:14.2(1)
课课练:14.2(1)
板书
设计
14.2(1)三角形的内角和
概念
1.三角形的内角和为
2.一个三角形中最多有____个锐角,
一个三角形中最多有____个直角,
一个三角形中最多有____个钝角
课后
反思
《三角形的内角和》教学反思
今天我讲了《三角形的内角和》一课,课前我分析:学生已经掌握了三角形的概念、分类,熟悉了钝角、锐角、平角这些角的知识。对于三角形的内角和是多少度,学生是不陌生的,因为学生有以前认识角、用量角器量三角板三个角的度数以及三角形的分类的基础,很多孩子都能回答出三角形的内角和是180度,但是他们却不知道怎样才能得出三角形的内角和是180度。
根据学情我设置了以下教学目标:
1、理解和掌握三角形的内角和性质;
2、经历对三角形内角和进行实验、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程;
3、体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义.体会化归、特殊到一般的数学思想和方程的思想。
在探究三角形的内角和时,我遵循由特殊到一般的认知规律,从学生熟悉的三角板入手抽象出特殊的三角形,计算出每块三角板的内角和是180°,接下来很自然地引导学生猜想:是不是所有的三角形的内角和都是180
°给学生提供一些材料,引导他们去探究出结论。学生任意画一个三角形进行验证,让学生经历从特殊到普遍的过程。这是动手操作的过程。因为前面没有试教过,所以在这里花的时间比较多,我自己觉得课上得有点拖,也有点沉闷。但在这一过程中,我也发现了很多的问题。很多学生是运用180度这个结论来量的。比如说他先量了二个角,最后一个角就不量了,直接用180度减去前面二个角,就是第三个角;还有很多同学,我让裁的是任意三角形,他们图方便全裁的直角三角形。我想如果这样的话就失去了测量的意义了。在交流的过程中,很多同学都说他们测量的结果是180度,导致另外一些不是180度的学生不敢表达自己的意见。我想面对这样的问题,如果我在交流反馈的时候,再多加一个环节,问你量出来的三个角分别是几度,内角和是几度,这样是不是会减少一些这样的问题。第二种方法是剪剪拼拼,我高估了学生的动手能力,几乎没有学生想到这种方法,其实可以直接告诉学生,剪下三个角来拼一拼,看看有什么发现。通过了解,其实有一些学生是知道的。如果我选用抛问题的方法,可能会出现一些亮点。下面在说理证明三角形内角和为180时,我提示学生添加辅助线平行线的方法,这样做让学生缺少了思考的机会,其实可以把整节课的大部分时间放在说理证明三角形内角和上,让学生们独立思考证明的方法,或许这样学生的参与度会更高,课堂氛围也能活跃起来。
整堂课下来,我自己觉得上得很沉闷,学生的注意力也不是非常集中,当然这和我自己有很大的关系,课堂气氛没能调节得很好。在自己的课中,我就觉得虽然验证的过程很严密,从特殊到普遍这样一个过程,但是留给学生思考的空间特别少,学生只是进行一些操作。总而言之,在上课的过程中,给了我一次学习的过程,在教案设计时,该怎么样把每一个环节落实到位,怎么样说好每一句话,预设好每一个环节。
1
