沪科版(2012)初中数学九年级下册 24.2.2 垂直与弦的直径 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.2.2 垂直与弦的直径 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览

文档简介
24.2.2
垂径定理
教学目标:
1、经历利用圆的轴对称性对垂径定理的探索和证明过程,掌握垂径定理;并能初步运用垂径定理解决有关的计算和证明问题;
2、在研究过程中,进一步体验“实验——归纳——猜测——证明”的方法;
3、让学生积极投入到圆的轴对称性的研究中,体验到垂径定理是圆的轴对称性质的重要体现。
教学重点:使学生掌握垂径定理、记住垂径定理的题设和结论。
教学难点:对垂径定理的探索和证明,并能应用垂径定理进行简单计算或证明。
教学用具:圆规,三角尺,几何画板课件
教学过程:
一、复习引入
1、我们已经学习了圆怎样的对称性质?
2、圆还有什么对称性质?作为轴对称图形,其对称轴是?(直径所在的直线)
3、观察并回答:
(1)在含有一条直径AB的圆上再增加一条直径CD,两条直径的位置关系?
(两条直径始终是互相平分的)
(2)把直径AB向下平移,变成非直径的弦,弦AB是否一定被直径CD平分?
二、新课
(一)猜想,证明,形成垂径定理
1、猜想:弦AB在怎样情况下会被直径CD平分?(当CD⊥AB时)(用课件观察翻折验证)
2、得出猜想:在圆⊙O中,CD是直径,AB是弦,当CD⊥AB时,弦AB会被直径CD平分。
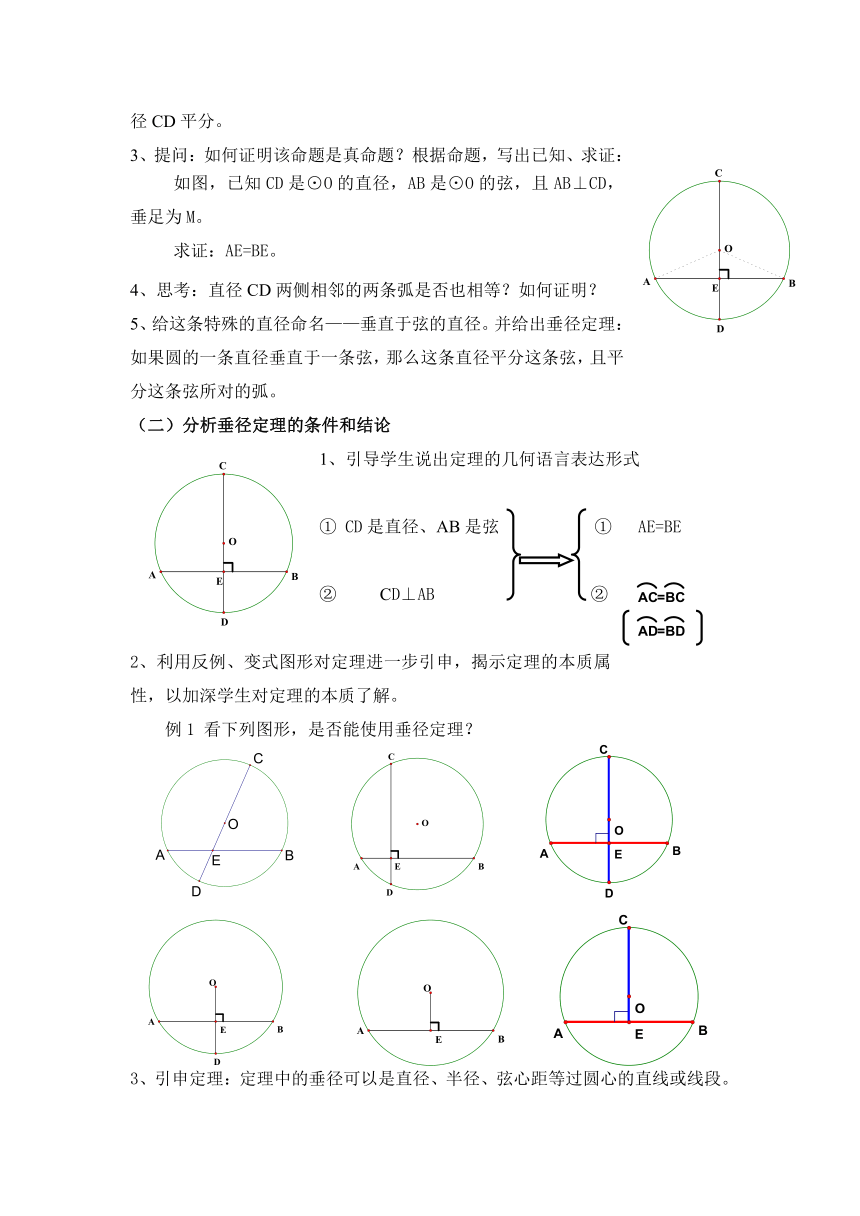
3、提问:如何证明该命题是真命题?根据命题,写出已知、求证:
如图,已知CD是⊙O的直径,AB是⊙O的弦,且AB⊥CD,垂足为M。
求证:AE=BE。
4、思考:直径CD两侧相邻的两条弧是否也相等?如何证明?
5、给这条特殊的直径命名——垂直于弦的直径。并给出垂径定理:如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,且平分这条弦所对的弧。
(二)分析垂径定理的条件和结论
1、引导学生说出定理的几何语言表达形式
①
CD是直径、AB是弦
①
AE=BE
②
CD⊥AB
②
2、利用反例、变式图形对定理进一步引申,揭示定理的本质属性,以加深学生对定理的本质了解。
例1
看下列图形,是否能使用垂径定理?
3、引申定理:定理中的垂径可以是直径、半径、弦心距等过圆心的直线或线段。从而得到垂径定理的变式:
①
经过圆心
得到
①
平分弦
一条直线具有:
②
垂直于弦
②
平分弦所对的劣(优)弧
(三)例题
例2
如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径
在例2图形的基础上:
变式(1)即例3
已知:如图,若以O为圆心作一个⊙O的同心圆,交大圆的弦AB于C,D两点。
求证:AC=BD。
(图1)
(图2)
变式(2)再添加一个同心圆,得(图2)则AC
BD
变式(3)隐去(图1)中的大圆,得(图3)连接OA,OB,设OA=OB,
求证:AC=BD。
变式(4)隐去(图1)中的大圆,得(图4)连接OC,OD,设OC=OD,
求证:AC=BD。
(图3)
(图4)
三、小结
1、这节课我们学习了哪些主要内容?
2、应用垂径定理要注意那些问题?
垂径定理的条件和结论:
①
经过圆心
得到
①
平分弦
一条直线具有:
②
垂直于弦
②
平分弦所对的劣(优)弧
3、思考:若将条件中的②与结论中的①互换,命题成立吗?
四、教后反思
本节课是在学生学习了过三点的圆和圆的有关性质等内容之后对垂直于弦的直径和这条弦的关系的进一步学习。垂径定理的推证是以圆是轴对称图形的性质为依据的,因此,垂径定理既是圆的性质---轴对称性质的重要体现,也是今后证明线段相等、角相等、弧相等、垂直关系的重要依据。本节内容是本章基础,是圆的有关计算和圆的有关证明的一个重要工具。同时,更为下节课垂径定理推论的引出奠定了基础。
本节课也存在着不足和需改进,甚至可以进一步完善之处:
(1)板书的设计。板书是无声的语言,是完成课堂教学任务的重要手段.板书也是教师的基本功之一。好的板书不仅有助于传授知识和方法,而且有助于启迪学生思维,有助于培养学生严肃认真的学习态度,养成良好的学习习惯;教师认真严谨、规范的板书是良好的示范,是言传身教的体现,不仅会起到让学生潜移默化的作用,而且还会给学生一种美的感受,增强学生的记忆效果、有利于学生的身心健康,陶冶学生的情操,培养严谨的治学精神。重视板书,研究板书,精心设计板书,对教师来讲是一项不可等闲视之的工作。在评课中我意识到为了进一步提高我的教学水平,我必须在板书的设计上下苦功,这也是我今后教学改进需努力的方向。对于新授课板书的设计上应精心布局,文字语言、符号语言、分析语言缺一不可,并且应该再配上基本图形以加深学生对定理的了解,除了突出要点,还需让学生感受到定理使用的规范性。这样不但能帮助学生了解和掌握教学的重点、难点,掌握知识的发展脉络和逻辑体系,更能调动学生多感官参加学习活动,使学生清晰地意识到实际的教学过程,启发学生的思维随着教学的进程而顺利发展。
(2)应适当地拔高学生对新课的理解体会。在新课引入部分证明直径平分弦这一结论时,不能只局限于学生得到添加半径作为辅助线这一结果上,而应利用这一机会帮助学生对之前所学的证明两条线段相等的几种方法进行回顾,以使证明方法系统化,不单纯为一节课服务。在垂径定理应用时,对于添加过圆心的垂线段的缘由也可以结合线段是轴对称图形,圆也是轴对称图形,而它们的公共对称轴即这条垂线段,帮助学生加深对轴对称图形添加辅助线的体会。
垂径定理
教学目标:
1、经历利用圆的轴对称性对垂径定理的探索和证明过程,掌握垂径定理;并能初步运用垂径定理解决有关的计算和证明问题;
2、在研究过程中,进一步体验“实验——归纳——猜测——证明”的方法;
3、让学生积极投入到圆的轴对称性的研究中,体验到垂径定理是圆的轴对称性质的重要体现。
教学重点:使学生掌握垂径定理、记住垂径定理的题设和结论。
教学难点:对垂径定理的探索和证明,并能应用垂径定理进行简单计算或证明。
教学用具:圆规,三角尺,几何画板课件
教学过程:
一、复习引入
1、我们已经学习了圆怎样的对称性质?
2、圆还有什么对称性质?作为轴对称图形,其对称轴是?(直径所在的直线)
3、观察并回答:
(1)在含有一条直径AB的圆上再增加一条直径CD,两条直径的位置关系?
(两条直径始终是互相平分的)
(2)把直径AB向下平移,变成非直径的弦,弦AB是否一定被直径CD平分?
二、新课
(一)猜想,证明,形成垂径定理
1、猜想:弦AB在怎样情况下会被直径CD平分?(当CD⊥AB时)(用课件观察翻折验证)
2、得出猜想:在圆⊙O中,CD是直径,AB是弦,当CD⊥AB时,弦AB会被直径CD平分。
3、提问:如何证明该命题是真命题?根据命题,写出已知、求证:
如图,已知CD是⊙O的直径,AB是⊙O的弦,且AB⊥CD,垂足为M。
求证:AE=BE。
4、思考:直径CD两侧相邻的两条弧是否也相等?如何证明?
5、给这条特殊的直径命名——垂直于弦的直径。并给出垂径定理:如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,且平分这条弦所对的弧。
(二)分析垂径定理的条件和结论
1、引导学生说出定理的几何语言表达形式
①
CD是直径、AB是弦
①
AE=BE
②
CD⊥AB
②
2、利用反例、变式图形对定理进一步引申,揭示定理的本质属性,以加深学生对定理的本质了解。
例1
看下列图形,是否能使用垂径定理?
3、引申定理:定理中的垂径可以是直径、半径、弦心距等过圆心的直线或线段。从而得到垂径定理的变式:
①
经过圆心
得到
①
平分弦
一条直线具有:
②
垂直于弦
②
平分弦所对的劣(优)弧
(三)例题
例2
如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径
在例2图形的基础上:
变式(1)即例3
已知:如图,若以O为圆心作一个⊙O的同心圆,交大圆的弦AB于C,D两点。
求证:AC=BD。
(图1)
(图2)
变式(2)再添加一个同心圆,得(图2)则AC
BD
变式(3)隐去(图1)中的大圆,得(图3)连接OA,OB,设OA=OB,
求证:AC=BD。
变式(4)隐去(图1)中的大圆,得(图4)连接OC,OD,设OC=OD,
求证:AC=BD。
(图3)
(图4)
三、小结
1、这节课我们学习了哪些主要内容?
2、应用垂径定理要注意那些问题?
垂径定理的条件和结论:
①
经过圆心
得到
①
平分弦
一条直线具有:
②
垂直于弦
②
平分弦所对的劣(优)弧
3、思考:若将条件中的②与结论中的①互换,命题成立吗?
四、教后反思
本节课是在学生学习了过三点的圆和圆的有关性质等内容之后对垂直于弦的直径和这条弦的关系的进一步学习。垂径定理的推证是以圆是轴对称图形的性质为依据的,因此,垂径定理既是圆的性质---轴对称性质的重要体现,也是今后证明线段相等、角相等、弧相等、垂直关系的重要依据。本节内容是本章基础,是圆的有关计算和圆的有关证明的一个重要工具。同时,更为下节课垂径定理推论的引出奠定了基础。
本节课也存在着不足和需改进,甚至可以进一步完善之处:
(1)板书的设计。板书是无声的语言,是完成课堂教学任务的重要手段.板书也是教师的基本功之一。好的板书不仅有助于传授知识和方法,而且有助于启迪学生思维,有助于培养学生严肃认真的学习态度,养成良好的学习习惯;教师认真严谨、规范的板书是良好的示范,是言传身教的体现,不仅会起到让学生潜移默化的作用,而且还会给学生一种美的感受,增强学生的记忆效果、有利于学生的身心健康,陶冶学生的情操,培养严谨的治学精神。重视板书,研究板书,精心设计板书,对教师来讲是一项不可等闲视之的工作。在评课中我意识到为了进一步提高我的教学水平,我必须在板书的设计上下苦功,这也是我今后教学改进需努力的方向。对于新授课板书的设计上应精心布局,文字语言、符号语言、分析语言缺一不可,并且应该再配上基本图形以加深学生对定理的了解,除了突出要点,还需让学生感受到定理使用的规范性。这样不但能帮助学生了解和掌握教学的重点、难点,掌握知识的发展脉络和逻辑体系,更能调动学生多感官参加学习活动,使学生清晰地意识到实际的教学过程,启发学生的思维随着教学的进程而顺利发展。
(2)应适当地拔高学生对新课的理解体会。在新课引入部分证明直径平分弦这一结论时,不能只局限于学生得到添加半径作为辅助线这一结果上,而应利用这一机会帮助学生对之前所学的证明两条线段相等的几种方法进行回顾,以使证明方法系统化,不单纯为一节课服务。在垂径定理应用时,对于添加过圆心的垂线段的缘由也可以结合线段是轴对称图形,圆也是轴对称图形,而它们的公共对称轴即这条垂线段,帮助学生加深对轴对称图形添加辅助线的体会。
