沪科版(2012)初中数学九年级下册 26.1 等可能情形下的概率计算 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 26.1 等可能情形下的概率计算 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 433.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 00:00:00 | ||
图片预览

文档简介
课题
26.2
等可能情形下的概率计算(2)
主备教师
备课时间
学科
数学
年级
九年级
教研组
数学教研组
教学目标
1.正确认识等可能情形下概率的意义,掌握简单随机事件概率的计算方法。
2.通过动手操作,培养学生参与、合作的精髓,感悟知识来源于生活,同时体会数学建模思想。
3.通过分析探究实践的概率,培养学生良好的动脑习惯,提高运用数学知识解决实际问题的意思,激发学生的学习兴趣。
教学重难点
教学重点
理解等可能情形下的随机事件的概率;
教学难点
理解等可能情形下的随机事件的概率;
教学方法
讲解、观察、思考、练习。
教学准备
多媒体课件。
教学过程
教学环节
教师活动
学生
目标引领
请同学来回答一下概率的定义及计算方法
观察
预学生疑
合作探究
例2
抛掷两枚均匀的硬币,求两枚硬币正面都向上的概率
解:
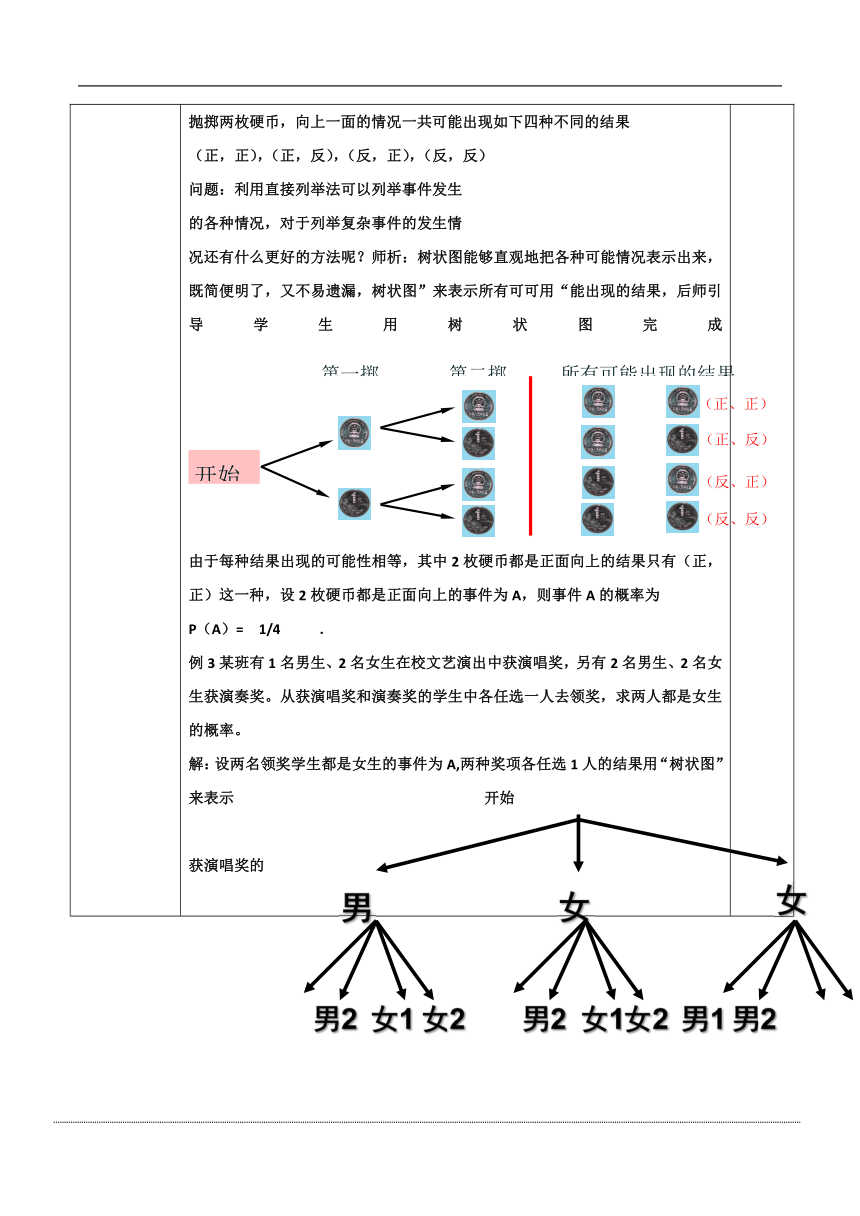
抛掷两枚硬币,向上一面的情况一共可能出现如下四种不同的结果
(正,正),(正,反),(反,正),(反,反)
问题:利用直接列举法可以列举事件发生
的各种情况,对于列举复杂事件的发生情
况还有什么更好的方法呢?师析:树状图能够直观地把各种可能情况表示出来,既简便明了,又不易遗漏,树状图”来表示所有可可用“能出现的结果,后师引导学生用树状图完成
由于每种结果出现的可能性相等,其中2枚硬币都是正面向上的结果只有(正,正)这一种,设2枚硬币都是正面向上的事件为A,则事件A的概率为
P(A)=
1/4
.
例3某班有1名男生、2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖。从获演唱奖和演奏奖的学生中各任选一人去领奖,求两人都是女生的概率。
解:设两名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示
开始
获演唱奖的
共有12中结果,且每种结果出现的可能性相等,其中2名都是女生的结果有4种,所以事件A发生的概率为P(A)=4/12=1/3
例
4
同时抛掷两枚均匀的骰子,骰子各面上的点数分别是1、2.。。。6
,试分别计算如下各随机事件的概率.
1)抛出的点数之和等于8;
2)抛出的点数之和等于12.
解
从上面表格中可以看到,同时抛掷两枚骰子,所有可能出现的结果共有36种,由于骰子是均匀的,所以每个结果出现的可能性相同
1)抛出的点数之和是8的结果有(2、6)、(3、5)、(4、4)、(5、3)、(6、2)五种,所以抛出的点数之和等于8这个事件发生的概率为5/36.
(2)抛出的点数之和等于12的结果仅有(6、6)一种,所以抛出的点数之和等于12这个事件的概率为1/36.
操作、观察总结
交流展示
(1)从一副扑克牌中选出4张K,洗匀后随机地抽取一张,请大家猜猜,这张会是什么K吗?那抽到方块K的概率是多少?
(2)从一副没有大小王的扑克牌(共52张)中随机地抽一张,问:
①可能抽到红桃的结果有多少个?其概率是多少呢?
②抽到Q牌的概率是多少?
学生操作回答
归纳提升
通过本节课的学习,你有哪些收获?
总结
评价反馈
习题26.2第1、2题
深化拓展
26.2
等可能情形下的概率计算(2)
主备教师
备课时间
学科
数学
年级
九年级
教研组
数学教研组
教学目标
1.正确认识等可能情形下概率的意义,掌握简单随机事件概率的计算方法。
2.通过动手操作,培养学生参与、合作的精髓,感悟知识来源于生活,同时体会数学建模思想。
3.通过分析探究实践的概率,培养学生良好的动脑习惯,提高运用数学知识解决实际问题的意思,激发学生的学习兴趣。
教学重难点
教学重点
理解等可能情形下的随机事件的概率;
教学难点
理解等可能情形下的随机事件的概率;
教学方法
讲解、观察、思考、练习。
教学准备
多媒体课件。
教学过程
教学环节
教师活动
学生
目标引领
请同学来回答一下概率的定义及计算方法
观察
预学生疑
合作探究
例2
抛掷两枚均匀的硬币,求两枚硬币正面都向上的概率
解:
抛掷两枚硬币,向上一面的情况一共可能出现如下四种不同的结果
(正,正),(正,反),(反,正),(反,反)
问题:利用直接列举法可以列举事件发生
的各种情况,对于列举复杂事件的发生情
况还有什么更好的方法呢?师析:树状图能够直观地把各种可能情况表示出来,既简便明了,又不易遗漏,树状图”来表示所有可可用“能出现的结果,后师引导学生用树状图完成
由于每种结果出现的可能性相等,其中2枚硬币都是正面向上的结果只有(正,正)这一种,设2枚硬币都是正面向上的事件为A,则事件A的概率为
P(A)=
1/4
.
例3某班有1名男生、2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖。从获演唱奖和演奏奖的学生中各任选一人去领奖,求两人都是女生的概率。
解:设两名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示
开始
获演唱奖的
共有12中结果,且每种结果出现的可能性相等,其中2名都是女生的结果有4种,所以事件A发生的概率为P(A)=4/12=1/3
例
4
同时抛掷两枚均匀的骰子,骰子各面上的点数分别是1、2.。。。6
,试分别计算如下各随机事件的概率.
1)抛出的点数之和等于8;
2)抛出的点数之和等于12.
解
从上面表格中可以看到,同时抛掷两枚骰子,所有可能出现的结果共有36种,由于骰子是均匀的,所以每个结果出现的可能性相同
1)抛出的点数之和是8的结果有(2、6)、(3、5)、(4、4)、(5、3)、(6、2)五种,所以抛出的点数之和等于8这个事件发生的概率为5/36.
(2)抛出的点数之和等于12的结果仅有(6、6)一种,所以抛出的点数之和等于12这个事件的概率为1/36.
操作、观察总结
交流展示
(1)从一副扑克牌中选出4张K,洗匀后随机地抽取一张,请大家猜猜,这张会是什么K吗?那抽到方块K的概率是多少?
(2)从一副没有大小王的扑克牌(共52张)中随机地抽一张,问:
①可能抽到红桃的结果有多少个?其概率是多少呢?
②抽到Q牌的概率是多少?
学生操作回答
归纳提升
通过本节课的学习,你有哪些收获?
总结
评价反馈
习题26.2第1、2题
深化拓展
