人教版七年级数学下册5.2.2 平行线的判定 课时练习(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册5.2.2 平行线的判定 课时练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 298.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-30 23:15:09 | ||
图片预览



文档简介
平行线的判定
课时练习
一、单选题
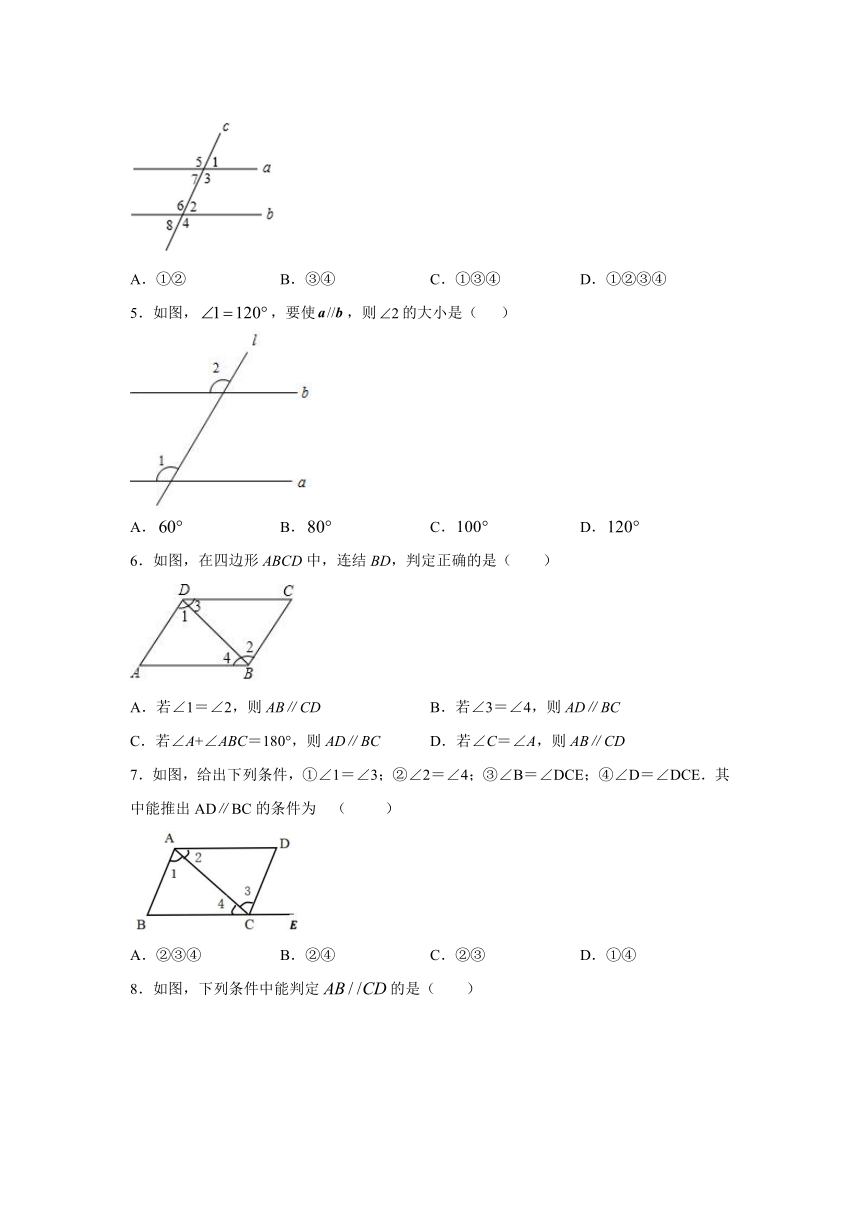
1.如图,,交于点,,,则的度数为(
).
A.
B.
C.
D.
2.如图,若
CD∥AB,则下列说法错误的是(
)
A.∠3=∠A
B.∠1=∠2
C.∠4=∠5
D.∠C+∠ABC=180°
3.如图∠1=∠2,则AB∥CD的根据是(
)
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角相等两直线平行
D.两直线平行,同位角相等
4.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a//b的条件是(
)
A.①②
B.③④
C.①③④
D.①②③④
5.如图,,要使,则的大小是(
)
A.
B.
C.
D.
6.如图,在四边形ABCD中,连结BD,判定正确的是( )
A.若∠1=∠2,则AB∥CD
B.若∠3=∠4,则AD∥BC
C.若∠A+∠ABC=180°,则AD∥BC
D.若∠C=∠A,则AB∥CD
7.如图,给出下列条件,①∠1=∠3;②∠2=∠4;③∠B=∠DCE;④∠D=∠DCE.其中能推出AD∥BC的条件为
(
)
A.②③④
B.②④
C.②③
D.①④
8.如图,下列条件中能判定的是(
)
A.
B.
C.
D.
9.下列说法错误的是(
)
A.两直线平行,内错角相等
B.两直线平行,同旁内角相等
C.同位角相等,两直线平行
D.平行于同一条直线的两直线平行
10.下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角必相等
B.如果两条直线被第三条直线所截,那么同位角的角平分线必平行
C.如果同旁内角互补,那么它们的角平分线必互相垂直
D.如果两角的两边分别平行,那么这两个角必相等
11.如图,下列条件能判定AB∥CD的是(
)
A.∠1=∠3
B.∠2=∠4
C.∠1=∠2
D.∠1+∠3=180°
12.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(
)
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.旁内角互补,两直线平行
D.两点确定一条直线
13.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠1+∠ACE=180°.其中,能判定AD∥BE的条件有(
)
A.2个
B.3个
C.4个
D.1个
14.以下条件中,不能判断图中的是(
)
A.
B.
C.
D.
15.如图,下列条件不能判定直线a∥b的是
A.∠1=∠3
B.∠2=∠4
C.∠2=∠3
D.∠2+∠3=180°
二、填空题
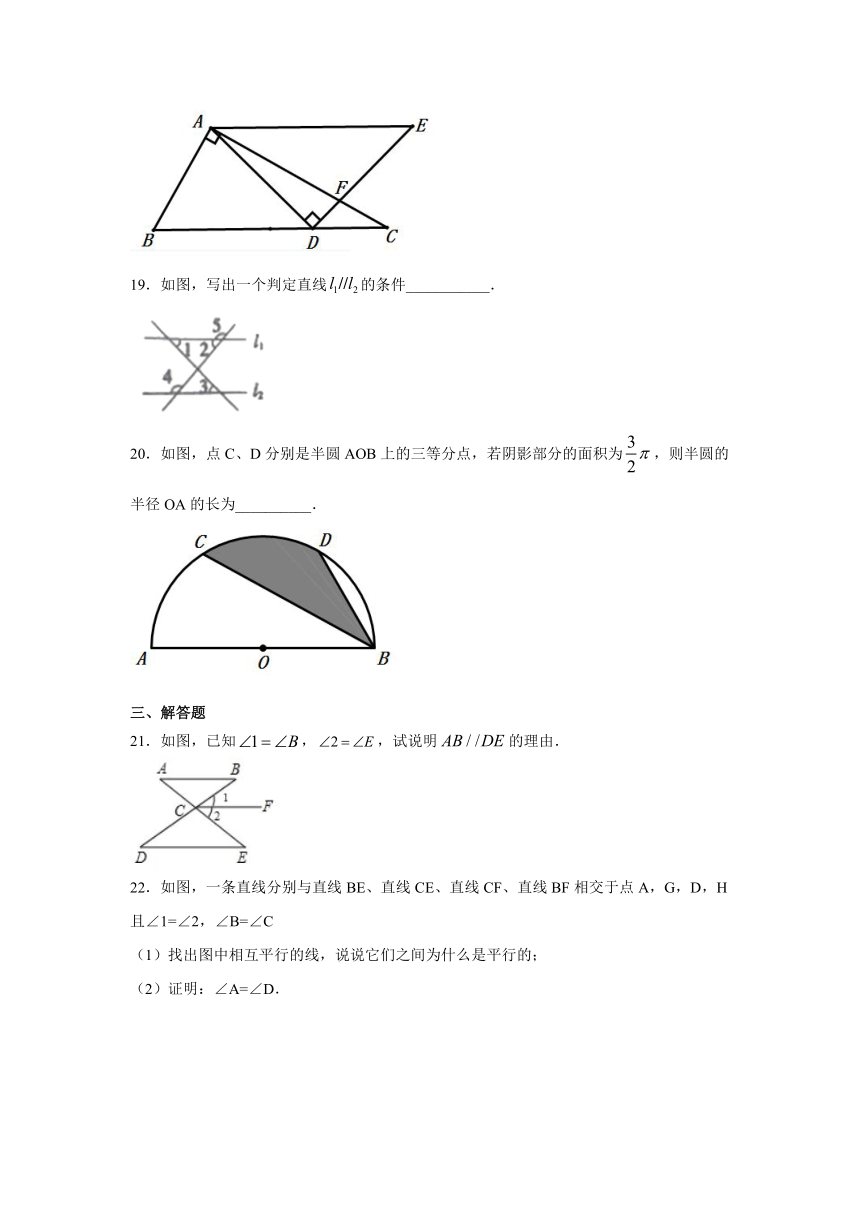
16.如图:已知:∠1=105°,∠2=105°,则_____∥_____.
17.已知,如图,要使得AB∥CD,你认为应该添加的一个条件是________
18.将一副三角形板按图所示放置,若AE∥BC,则∠BAD=____
19.如图,写出一个判定直线的条件___________.
20.如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为,则半圆的半径OA的长为__________.
三、解答题
21.如图,已知,,试说明的理由.
22.如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
23.如图,△ABC中,∠B=∠ACB,D在BC的延长线,CD平分∠ECF,求证:AB//CE.
24.如图,∠1=80°,∠2=100°,∠3=75°,求∠4的度数.
25.如图,直线AB过点C,∠2=80°,∠D=50°,∠1=∠3,AB∥DE吗?为什么?
参考答案
1.A
∵
∴
∴
∴
2.C
∵CD∥AB,
∴∠3=∠A,∠1=∠2,∠C+∠ABC=180°,
故选C.
∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选:B.
4.D
①∵∠1=∠2,
∴a//b(同位角相等,两直线平行);
②∵∠3=∠6,
∴a//b(内错角相等,两直线平行);
③∵∠4=∠6(对顶角),
又∵∠4+∠7=180°,
∴∠6+∠7=180°(等角的补角相等),
∴a//b(同旁内角互补,两直线平行);
④∵∠5+∠7=180°(邻补角),
又∵∠5+∠8=180°,
∴∠7=∠8(等角的补角相等),
∴a//b(同位角相等,两直线平行);
故选D.
D
如果,
那么.
所以要使,则的大小是.
6.C
解:A、根据∠1=∠2不能推出AB∥CD,故本选项不符合题意;
B、根据∠3=∠4不能推出AD∥BC,故本选项不符合题意;
C、根据∠A+∠ABC=180°能推出AD∥BC,故本选项符合题意;
D、根据∠C=∠A不能推出AB∥CD,故本选项不符合题意.
故选:C.
7.B
∵∠1=∠3,∴AB∥CD,故①不符合题意;
∵∠2=∠4,∴AD∥BC,故②符合题意;
∵∠B=∠DCE,∴AB∥CD,故③不符合题意;
∵∠D=∠DCE,∴AD∥BC,故④符合题意;
综上所述,②④符合题意,
故选:B.
8.D
A、根据同旁内角互补,两直线平行的判定定理可知不能判定;
B、
和为对顶角,无法判定;
C、根据同位角相等,两直线平行的判定定理可知不能判定;
D、根据内错角相等,两直线平行的判定定理可知可得.
故选:D.
9.B
A选项中,“两直线平行,内错角相等”是正确的,所以不能选A;
B选项中,“两直线平行,同旁内角相等”是错误的,所以可以选B;
C选项中,“同位角相等,两直线平行”是正确的,所以不能选C;
D选项中,“平行于同一直线的两直线平行”是正确的,所以不能选D.
故选:B.
10.C
A.
两条被截直线平行时,内错角相等,故本选项错误;
B.
如果两条相互平行直线被第三条直线所截,那么同位角的角平分线必平行,故本选项错误;
C.
如果同旁内角互补,那么这个角的两条边相互平行,则它们的角平分线必互相垂直,故本选项正确;
D.
如果两角的两边分别平行,那么这两个角相等或互补,故本选项错误;
故选C.
11.A
A.
由同位角相等两直线平行可知∠1=∠3时,AB∥CD,故A正确,D错误;
B.
由同旁内角互补,两直线平行可知∠2+∠4=180°时,AB∥CD,故B错误;
C.
由于∠1与∠2是对顶角,所以∠1=∠2不能判定AB∥CD,故C错误;
故选A.
12.A
由图形得,有两个相等的同位角,所以只能依据:同位角相等,两直线平行,
故选:.
13.A
①由∠1=∠2,可得AD∥BE;
②由∠3=∠4,可得AB∥CD,不能得到AD∥BE;
③由∠B=∠5,可得AB∥CD,不能得到AD∥BE;
④由∠1+∠ACE=180°,可得AD∥BE.
故选A.
14.A
A、∵∠1=∠2,∴AD∥BC,符合题意;
B、∵∠2=∠4,∴AB∥CD,不符合题意;
C、∵∠1=∠A,∴AB∥CD,不符合题意;
D、∵∠2+∠3=180°,∴AB∥CD,不符合题意.
故选:A.
15.C
A.
∵
,
∴a∥b(两同位角相等,两直线平行);
故A能;
B.
∵,
∴a∥b(两同位角相等,两直线平行);
故B能;
C.
由不能判定a∥b,故C不能;
D.
∵.
∴a∥b(同旁内角互补,两直线平行);
故D能;
故选C.
16.a??
b
∵∠1=105°,∠2=105°,∴∠1=∠2,∴a∥b.
故答案为a,b.
17.∠ECD=∠A(答案不唯一).
添加的条件是:∠ECD=∠A(答案不唯一).
故答案为:∠ECD=∠A.
18.75°
由题意,∠B=60?,∠DAE=45?,
∵AE∥BC,
∴∠ADB=∠DAE=45?,
∴∠BAD=180?﹣∠B﹣∠ADB
=180?﹣60?﹣45?
=75?,
故答案为:75?.
19.∠1=∠3
当∠1=∠3或∠2+∠4=180°或∠4=∠5时,都可以得出直线l1∥l2.
故答案为:∠1=∠3(答案不唯一).
20.
如图,连接
点C、D分别是半圆AOB上的三等分点,
为等边三角形,
解得:
(负根舍去),
故答案为:
21解:理由如下:
∵,
∴AB∥CF,
∵,
∴CF∥DE,
∴AB∥DE.
22.(1)CE∥BF,AB∥CD.理由见解析.(2)证明见解析.
(1)CE∥BF,AB∥CD.理由:
∵∠1=∠2,
∴CE∥FB,
∴∠C=∠BFD,
∵∠B=∠C,
∴∠B=∠BFD,
∴AB∥CD;
(2)由(1)可得AB∥CD,
∴∠A=∠D.
23.证明:因为∠ACB与∠DCF是对顶角,
所以∠ACB=∠DCF,
又因为∠B=∠ACB,
所以∠B=∠DCF,
因为CD平分∠ECF,
所以∠DCF=∠ECD
所以∠B=∠ECD
所以AB//CE.
24.75°
∵∠2=100°,
∴∠5=180°-∠2=80°,
∴∠1=∠5,
∴a∥b,
∴∠4=∠3=75°
25.∵∠2=80°,∠1=∠3(已知)
∠1+∠2+∠3=180°(平角定义)
∴∠1=∠3=50°
又∵∠D=50°(已知)
∴∠1=∠D(等量代换)
∴AB∥DE(内错角相等,两直线平行).
课时练习
一、单选题
1.如图,,交于点,,,则的度数为(
).
A.
B.
C.
D.
2.如图,若
CD∥AB,则下列说法错误的是(
)
A.∠3=∠A
B.∠1=∠2
C.∠4=∠5
D.∠C+∠ABC=180°
3.如图∠1=∠2,则AB∥CD的根据是(
)
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角相等两直线平行
D.两直线平行,同位角相等
4.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a//b的条件是(
)
A.①②
B.③④
C.①③④
D.①②③④
5.如图,,要使,则的大小是(
)
A.
B.
C.
D.
6.如图,在四边形ABCD中,连结BD,判定正确的是( )
A.若∠1=∠2,则AB∥CD
B.若∠3=∠4,则AD∥BC
C.若∠A+∠ABC=180°,则AD∥BC
D.若∠C=∠A,则AB∥CD
7.如图,给出下列条件,①∠1=∠3;②∠2=∠4;③∠B=∠DCE;④∠D=∠DCE.其中能推出AD∥BC的条件为
(
)
A.②③④
B.②④
C.②③
D.①④
8.如图,下列条件中能判定的是(
)
A.
B.
C.
D.
9.下列说法错误的是(
)
A.两直线平行,内错角相等
B.两直线平行,同旁内角相等
C.同位角相等,两直线平行
D.平行于同一条直线的两直线平行
10.下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角必相等
B.如果两条直线被第三条直线所截,那么同位角的角平分线必平行
C.如果同旁内角互补,那么它们的角平分线必互相垂直
D.如果两角的两边分别平行,那么这两个角必相等
11.如图,下列条件能判定AB∥CD的是(
)
A.∠1=∠3
B.∠2=∠4
C.∠1=∠2
D.∠1+∠3=180°
12.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(
)
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.旁内角互补,两直线平行
D.两点确定一条直线
13.如图,下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠1+∠ACE=180°.其中,能判定AD∥BE的条件有(
)
A.2个
B.3个
C.4个
D.1个
14.以下条件中,不能判断图中的是(
)
A.
B.
C.
D.
15.如图,下列条件不能判定直线a∥b的是
A.∠1=∠3
B.∠2=∠4
C.∠2=∠3
D.∠2+∠3=180°
二、填空题
16.如图:已知:∠1=105°,∠2=105°,则_____∥_____.
17.已知,如图,要使得AB∥CD,你认为应该添加的一个条件是________
18.将一副三角形板按图所示放置,若AE∥BC,则∠BAD=____
19.如图,写出一个判定直线的条件___________.
20.如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为,则半圆的半径OA的长为__________.
三、解答题
21.如图,已知,,试说明的理由.
22.如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
23.如图,△ABC中,∠B=∠ACB,D在BC的延长线,CD平分∠ECF,求证:AB//CE.
24.如图,∠1=80°,∠2=100°,∠3=75°,求∠4的度数.
25.如图,直线AB过点C,∠2=80°,∠D=50°,∠1=∠3,AB∥DE吗?为什么?
参考答案
1.A
∵
∴
∴
∴
2.C
∵CD∥AB,
∴∠3=∠A,∠1=∠2,∠C+∠ABC=180°,
故选C.
∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选:B.
4.D
①∵∠1=∠2,
∴a//b(同位角相等,两直线平行);
②∵∠3=∠6,
∴a//b(内错角相等,两直线平行);
③∵∠4=∠6(对顶角),
又∵∠4+∠7=180°,
∴∠6+∠7=180°(等角的补角相等),
∴a//b(同旁内角互补,两直线平行);
④∵∠5+∠7=180°(邻补角),
又∵∠5+∠8=180°,
∴∠7=∠8(等角的补角相等),
∴a//b(同位角相等,两直线平行);
故选D.
D
如果,
那么.
所以要使,则的大小是.
6.C
解:A、根据∠1=∠2不能推出AB∥CD,故本选项不符合题意;
B、根据∠3=∠4不能推出AD∥BC,故本选项不符合题意;
C、根据∠A+∠ABC=180°能推出AD∥BC,故本选项符合题意;
D、根据∠C=∠A不能推出AB∥CD,故本选项不符合题意.
故选:C.
7.B
∵∠1=∠3,∴AB∥CD,故①不符合题意;
∵∠2=∠4,∴AD∥BC,故②符合题意;
∵∠B=∠DCE,∴AB∥CD,故③不符合题意;
∵∠D=∠DCE,∴AD∥BC,故④符合题意;
综上所述,②④符合题意,
故选:B.
8.D
A、根据同旁内角互补,两直线平行的判定定理可知不能判定;
B、
和为对顶角,无法判定;
C、根据同位角相等,两直线平行的判定定理可知不能判定;
D、根据内错角相等,两直线平行的判定定理可知可得.
故选:D.
9.B
A选项中,“两直线平行,内错角相等”是正确的,所以不能选A;
B选项中,“两直线平行,同旁内角相等”是错误的,所以可以选B;
C选项中,“同位角相等,两直线平行”是正确的,所以不能选C;
D选项中,“平行于同一直线的两直线平行”是正确的,所以不能选D.
故选:B.
10.C
A.
两条被截直线平行时,内错角相等,故本选项错误;
B.
如果两条相互平行直线被第三条直线所截,那么同位角的角平分线必平行,故本选项错误;
C.
如果同旁内角互补,那么这个角的两条边相互平行,则它们的角平分线必互相垂直,故本选项正确;
D.
如果两角的两边分别平行,那么这两个角相等或互补,故本选项错误;
故选C.
11.A
A.
由同位角相等两直线平行可知∠1=∠3时,AB∥CD,故A正确,D错误;
B.
由同旁内角互补,两直线平行可知∠2+∠4=180°时,AB∥CD,故B错误;
C.
由于∠1与∠2是对顶角,所以∠1=∠2不能判定AB∥CD,故C错误;
故选A.
12.A
由图形得,有两个相等的同位角,所以只能依据:同位角相等,两直线平行,
故选:.
13.A
①由∠1=∠2,可得AD∥BE;
②由∠3=∠4,可得AB∥CD,不能得到AD∥BE;
③由∠B=∠5,可得AB∥CD,不能得到AD∥BE;
④由∠1+∠ACE=180°,可得AD∥BE.
故选A.
14.A
A、∵∠1=∠2,∴AD∥BC,符合题意;
B、∵∠2=∠4,∴AB∥CD,不符合题意;
C、∵∠1=∠A,∴AB∥CD,不符合题意;
D、∵∠2+∠3=180°,∴AB∥CD,不符合题意.
故选:A.
15.C
A.
∵
,
∴a∥b(两同位角相等,两直线平行);
故A能;
B.
∵,
∴a∥b(两同位角相等,两直线平行);
故B能;
C.
由不能判定a∥b,故C不能;
D.
∵.
∴a∥b(同旁内角互补,两直线平行);
故D能;
故选C.
16.a??
b
∵∠1=105°,∠2=105°,∴∠1=∠2,∴a∥b.
故答案为a,b.
17.∠ECD=∠A(答案不唯一).
添加的条件是:∠ECD=∠A(答案不唯一).
故答案为:∠ECD=∠A.
18.75°
由题意,∠B=60?,∠DAE=45?,
∵AE∥BC,
∴∠ADB=∠DAE=45?,
∴∠BAD=180?﹣∠B﹣∠ADB
=180?﹣60?﹣45?
=75?,
故答案为:75?.
19.∠1=∠3
当∠1=∠3或∠2+∠4=180°或∠4=∠5时,都可以得出直线l1∥l2.
故答案为:∠1=∠3(答案不唯一).
20.
如图,连接
点C、D分别是半圆AOB上的三等分点,
为等边三角形,
解得:
(负根舍去),
故答案为:
21解:理由如下:
∵,
∴AB∥CF,
∵,
∴CF∥DE,
∴AB∥DE.
22.(1)CE∥BF,AB∥CD.理由见解析.(2)证明见解析.
(1)CE∥BF,AB∥CD.理由:
∵∠1=∠2,
∴CE∥FB,
∴∠C=∠BFD,
∵∠B=∠C,
∴∠B=∠BFD,
∴AB∥CD;
(2)由(1)可得AB∥CD,
∴∠A=∠D.
23.证明:因为∠ACB与∠DCF是对顶角,
所以∠ACB=∠DCF,
又因为∠B=∠ACB,
所以∠B=∠DCF,
因为CD平分∠ECF,
所以∠DCF=∠ECD
所以∠B=∠ECD
所以AB//CE.
24.75°
∵∠2=100°,
∴∠5=180°-∠2=80°,
∴∠1=∠5,
∴a∥b,
∴∠4=∠3=75°
25.∵∠2=80°,∠1=∠3(已知)
∠1+∠2+∠3=180°(平角定义)
∴∠1=∠3=50°
又∵∠D=50°(已知)
∴∠1=∠D(等量代换)
∴AB∥DE(内错角相等,两直线平行).
