算法小结
图片预览



文档简介
(共26张PPT)
算法初步单元小结
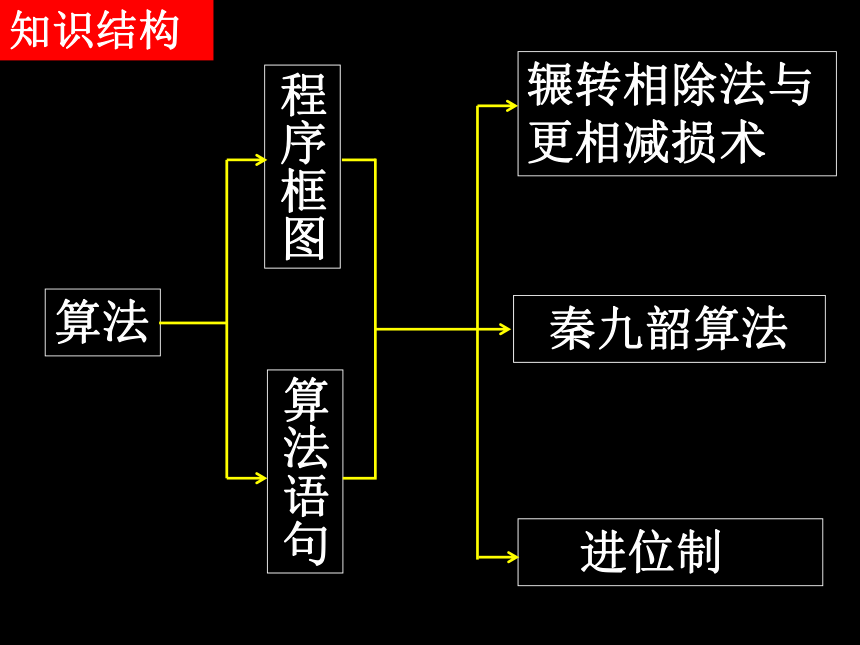
知识结构
算法
程序框图
算法语句
辗转相除法与更相减损术
秦九韶算法
进位制
知识梳理
1.算法的概念
在数学中,按照一定规则解决某一类问题的明确和有限的步骤称为算法.
用程序框、流程线及文字说明来表示算法的图形称为程序框图.
2.程序框图的概念
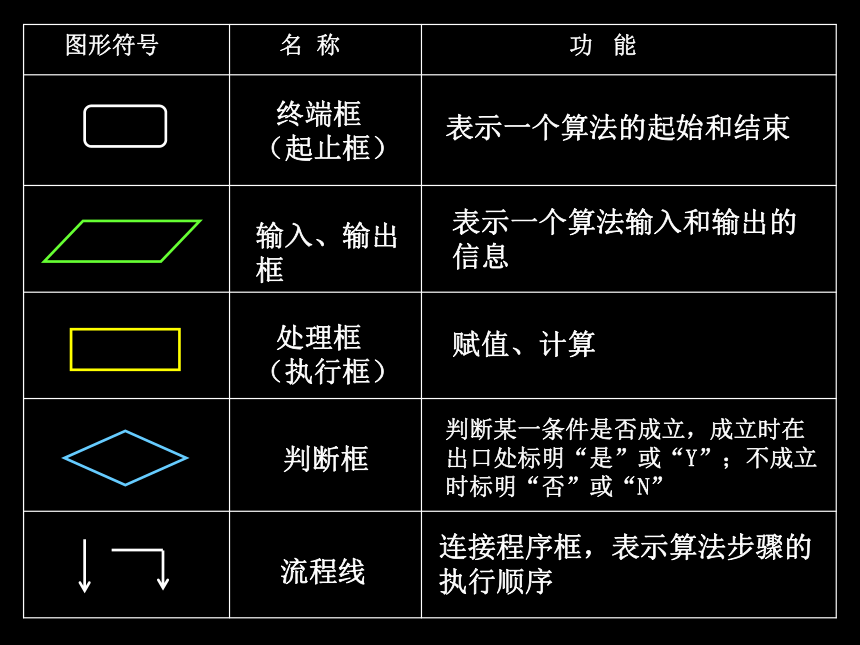
3.程序框、流程线的名称与功能
图形符号
名 称
功 能
终端框 (起止框)
输入、输出框
处理框 (执行框)
判断框
流程线
表示一个算法的起始和结束
表示一个算法输入和输出的信息
赋值、计算
判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”
连接程序框,表示算法步骤的执行顺序
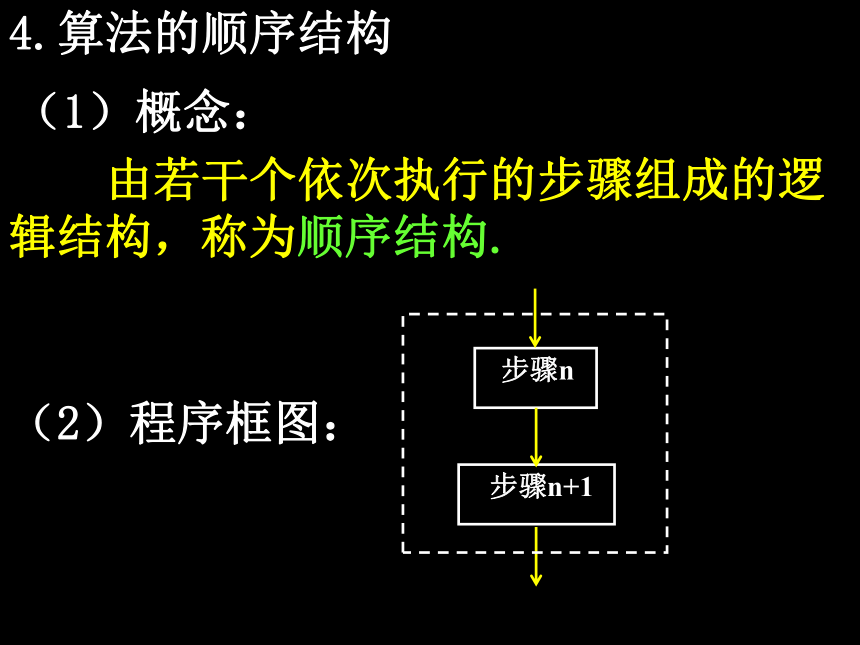
4.算法的顺序结构
(1)概念:
由若干个依次执行的步骤组成的逻辑结构,称为顺序结构.
(2)程序框图:
步骤n
步骤n+1
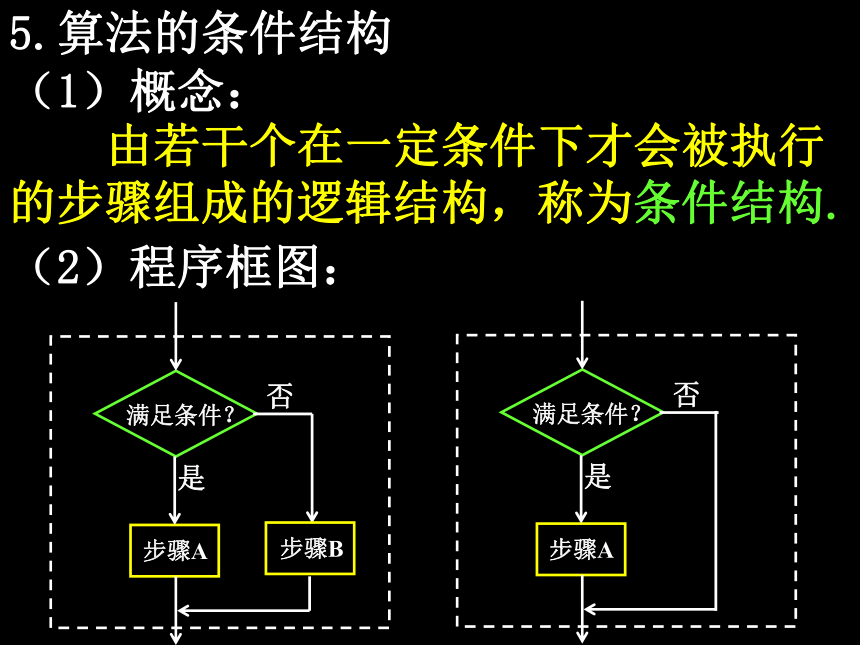
5.算法的条件结构
(1)概念:
由若干个在一定条件下才会被执行的步骤组成的逻辑结构,称为条件结构.
(2)程序框图:
满足条件?
步骤A
步骤B
是
否
满足条件?
步骤A
是
否
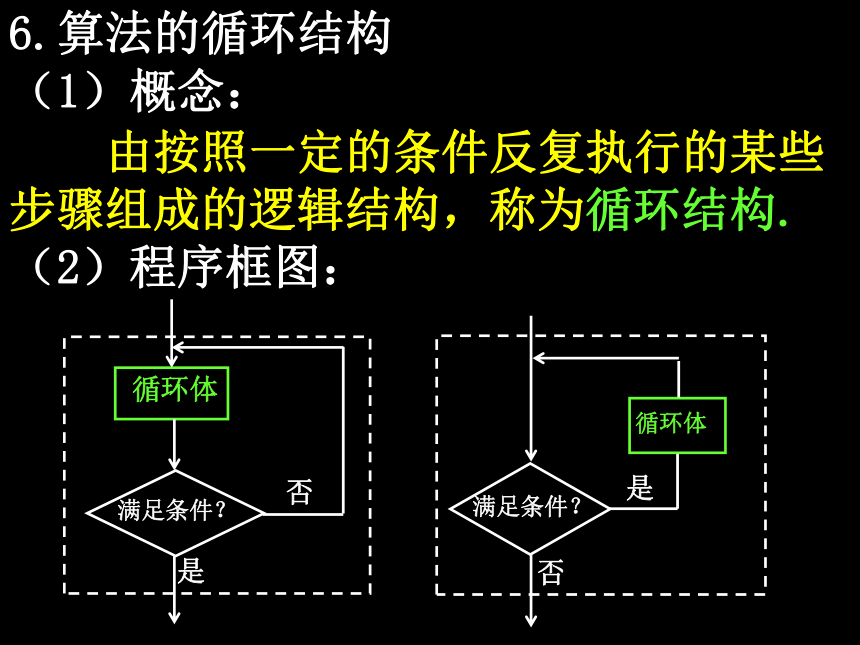
6.算法的循环结构
(1)概念:
由按照一定的条件反复执行的某些步骤组成的逻辑结构,称为循环结构.
(2)程序框图:
循环体
满足条件?
是
否
循环体
满足条件?
是
否
7.算法的输入语句
INPUT “提示内容”;变量
8.算法的输出语句
PRINT “提示内容”;表达式
9.算法的赋值语句
变量=表达式
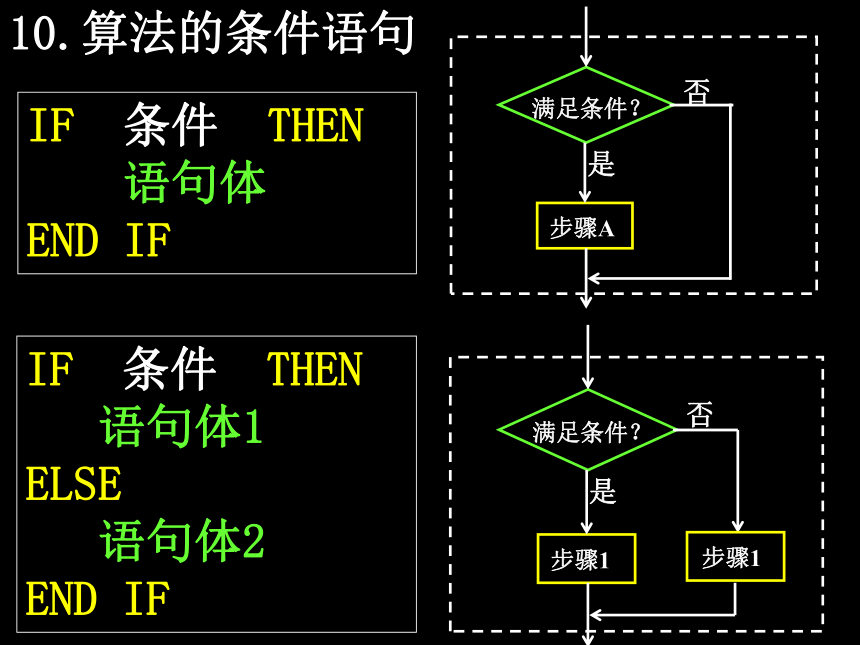
10.算法的条件语句
IF 条件 THEN
语句体
END IF
IF 条件 THEN
语句体1
ELSE
语句体2
END IF
满足条件?
步骤1
步骤1
是
否
满足条件?
步骤A
是
否
11.算法的循环语句
DO
循环体
LOOP UNTIL 条件
满足条件?
是
循环体
否
WHILE 条件
循环体
WEND
循环体
满足条件?
是
否
12.辗转相除法
第一步,给定两个正整数m,n(m>n).
第二步,计算m除以n所得的余数r.
第三步,m=n,n=r.
第四步,若r=0,则m,n的最大公约数等 于m;否则,返回第二步.
求两个正整数的最大公约数
13.更相减损术
第一步,给定两个正整数m,n(m>n).
第二步,计算m-n所得的差k.
第三步,比较n与k的大小,其中大者用m表 示,小者用n表示.
第四步,若m=n,则m,n的最大公约数等于 m;否则,返回第二步.
求两个正整数的最大公约数
14.秦九韶算法
第一步,输入多项式的次数n,最高次 项的系数an和x的值.
第二步,令v=an,i=n-1.
第三步,输入i次项的系数ai.
第四步,v=vx+ai,i=i-1.
第五步,判断i≥0是否成立.若是,则返回第 二步;否则,输出多项式的值v.
求多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值
15.k进制化十进制的算法
第四步,判断i>n 是否成立.若是,则 输出b的值;否则,返回第三步.
第一步,输入a,k和n的值.
第二步,令b=0,i=1.
第三步, ,i=i+1.
anan-1…a1a0(k)
=an×kn+ an×kn-1+…a1×k1+ a0×k0
16. 十进制化k进制的算法
第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.
第一步,输入十进制数a和基数k的值.
第二步,求出a除以k所得的商q,余数r.
第三步,把所得的余数依次从右到左排 列.
除k取余法
一、考查程序框图、语句的功能
例1、如图给出了一个算法流程图,该算法流程
图的功能是( )
A.求a,b,c三数的最大数
B.求a,b,c三数的最小数
C.将a,b,c按从小到大排序
D.将a,b,c按从大到小排序
例2、如图是一个算法的程序框图,当输入
的值x为5时,则其输出的结果是 。
例3、根据框图,回答下列问题:
(1)若输入的x值为5,
则输出的结果是: ;
(2)要输出的值为8,
则输入的x是 ;
(3)要使输出的值最小,
输入的x的范围是 。
二、完善程序框图中的条件或内容
例4、如图,若框图所给的程序运行结果为s=132,那么判断框中应填入的关于k的判断条件是 。
例5、上图是的程序框图,判断框应填入的内容
是 ,处理框应填入的内容是 。
三、算法与其他知识的综合
例6、如图是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为A1、A2、…A10(如A2表示身高(单位:cm)在[150,155 内的人数。图2是统计图1中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
(A)i<6 (B) i<7 (C) i<8 (D) i<9
例7、阅读程序框图,若输入的是100,则输出
的变量和的值依次是( )
A.2500,2500
B.2550,2550
C.2500,2550
D.2550,2500
例8、甲、乙两人玩游戏,规则如流程图所示,
则甲胜的概率是 。
例9、阅读图中的流程图,回答下面问题:
1.若a<b<c,则输出的数是 ;
2.若 ,则输出的数是 。
例10、为确保信息安全,信息需要加密传输,发送方由明文密文(加密),接受方有密文明文(解密),已知加密规则如图所示,例如,输入明文1,2,3,4则对应加密文5,7,18,16。若接受方收到密文14,9,23,28时,则解密得到的明文为:( )
A.4,6,1,7
B.7,6,1,4
C.6,4,1,7
D.1,6,4,7
算法初步单元小结
知识结构
算法
程序框图
算法语句
辗转相除法与更相减损术
秦九韶算法
进位制
知识梳理
1.算法的概念
在数学中,按照一定规则解决某一类问题的明确和有限的步骤称为算法.
用程序框、流程线及文字说明来表示算法的图形称为程序框图.
2.程序框图的概念
3.程序框、流程线的名称与功能
图形符号
名 称
功 能
终端框 (起止框)
输入、输出框
处理框 (执行框)
判断框
流程线
表示一个算法的起始和结束
表示一个算法输入和输出的信息
赋值、计算
判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”
连接程序框,表示算法步骤的执行顺序
4.算法的顺序结构
(1)概念:
由若干个依次执行的步骤组成的逻辑结构,称为顺序结构.
(2)程序框图:
步骤n
步骤n+1
5.算法的条件结构
(1)概念:
由若干个在一定条件下才会被执行的步骤组成的逻辑结构,称为条件结构.
(2)程序框图:
满足条件?
步骤A
步骤B
是
否
满足条件?
步骤A
是
否
6.算法的循环结构
(1)概念:
由按照一定的条件反复执行的某些步骤组成的逻辑结构,称为循环结构.
(2)程序框图:
循环体
满足条件?
是
否
循环体
满足条件?
是
否
7.算法的输入语句
INPUT “提示内容”;变量
8.算法的输出语句
PRINT “提示内容”;表达式
9.算法的赋值语句
变量=表达式
10.算法的条件语句
IF 条件 THEN
语句体
END IF
IF 条件 THEN
语句体1
ELSE
语句体2
END IF
满足条件?
步骤1
步骤1
是
否
满足条件?
步骤A
是
否
11.算法的循环语句
DO
循环体
LOOP UNTIL 条件
满足条件?
是
循环体
否
WHILE 条件
循环体
WEND
循环体
满足条件?
是
否
12.辗转相除法
第一步,给定两个正整数m,n(m>n).
第二步,计算m除以n所得的余数r.
第三步,m=n,n=r.
第四步,若r=0,则m,n的最大公约数等 于m;否则,返回第二步.
求两个正整数的最大公约数
13.更相减损术
第一步,给定两个正整数m,n(m>n).
第二步,计算m-n所得的差k.
第三步,比较n与k的大小,其中大者用m表 示,小者用n表示.
第四步,若m=n,则m,n的最大公约数等于 m;否则,返回第二步.
求两个正整数的最大公约数
14.秦九韶算法
第一步,输入多项式的次数n,最高次 项的系数an和x的值.
第二步,令v=an,i=n-1.
第三步,输入i次项的系数ai.
第四步,v=vx+ai,i=i-1.
第五步,判断i≥0是否成立.若是,则返回第 二步;否则,输出多项式的值v.
求多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值
15.k进制化十进制的算法
第四步,判断i>n 是否成立.若是,则 输出b的值;否则,返回第三步.
第一步,输入a,k和n的值.
第二步,令b=0,i=1.
第三步, ,i=i+1.
anan-1…a1a0(k)
=an×kn+ an×kn-1+…a1×k1+ a0×k0
16. 十进制化k进制的算法
第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.
第一步,输入十进制数a和基数k的值.
第二步,求出a除以k所得的商q,余数r.
第三步,把所得的余数依次从右到左排 列.
除k取余法
一、考查程序框图、语句的功能
例1、如图给出了一个算法流程图,该算法流程
图的功能是( )
A.求a,b,c三数的最大数
B.求a,b,c三数的最小数
C.将a,b,c按从小到大排序
D.将a,b,c按从大到小排序
例2、如图是一个算法的程序框图,当输入
的值x为5时,则其输出的结果是 。
例3、根据框图,回答下列问题:
(1)若输入的x值为5,
则输出的结果是: ;
(2)要输出的值为8,
则输入的x是 ;
(3)要使输出的值最小,
输入的x的范围是 。
二、完善程序框图中的条件或内容
例4、如图,若框图所给的程序运行结果为s=132,那么判断框中应填入的关于k的判断条件是 。
例5、上图是的程序框图,判断框应填入的内容
是 ,处理框应填入的内容是 。
三、算法与其他知识的综合
例6、如图是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为A1、A2、…A10(如A2表示身高(单位:cm)在[150,155 内的人数。图2是统计图1中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
(A)i<6 (B) i<7 (C) i<8 (D) i<9
例7、阅读程序框图,若输入的是100,则输出
的变量和的值依次是( )
A.2500,2500
B.2550,2550
C.2500,2550
D.2550,2500
例8、甲、乙两人玩游戏,规则如流程图所示,
则甲胜的概率是 。
例9、阅读图中的流程图,回答下面问题:
1.若a<b<c,则输出的数是 ;
2.若 ,则输出的数是 。
例10、为确保信息安全,信息需要加密传输,发送方由明文密文(加密),接受方有密文明文(解密),已知加密规则如图所示,例如,输入明文1,2,3,4则对应加密文5,7,18,16。若接受方收到密文14,9,23,28时,则解密得到的明文为:( )
A.4,6,1,7
B.7,6,1,4
C.6,4,1,7
D.1,6,4,7
