3.3几何概型2
图片预览






文档简介
(共24张PPT)
(第一课时)
复习
古典概型的两个基本特点:
(1)所有的基本事件只有有限个;
(2)每个基本事件发生都是等可能的.
那么对于有无限多个试验结果的情况相应的概率应如果求呢
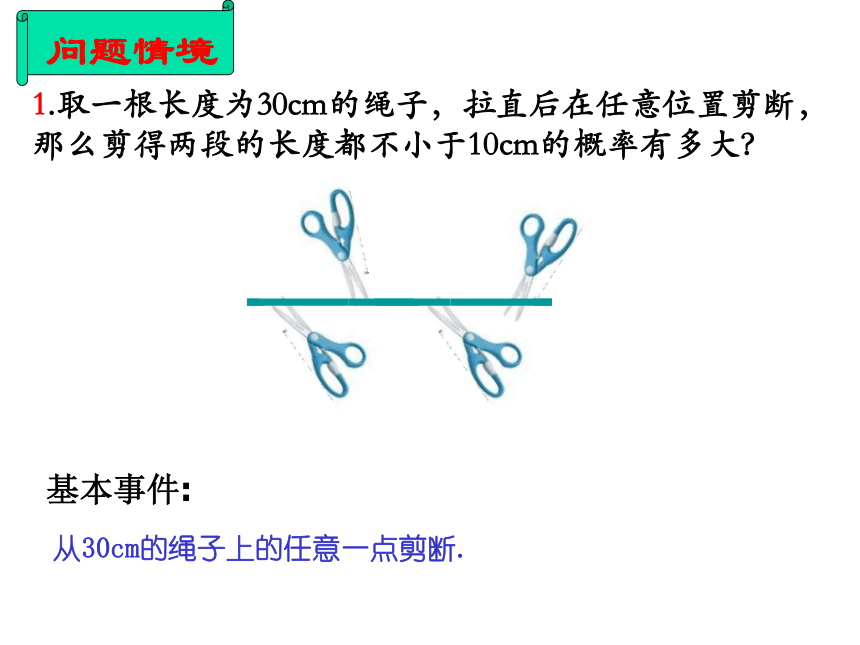
1.取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?
从30cm的绳子上的任意一点剪断.
基本事件:
问题情境
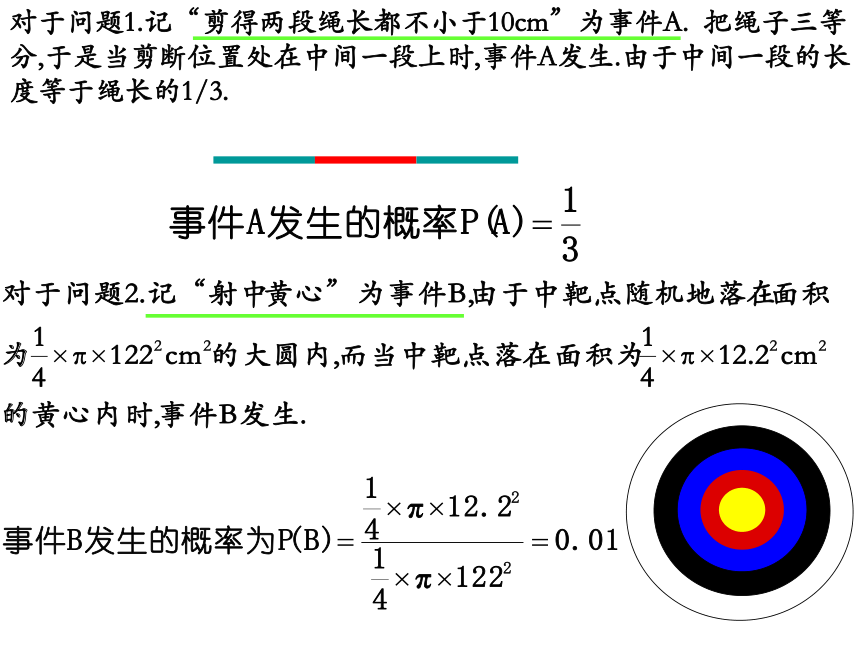
2.射箭比赛的箭靶是涂有五个彩色的分环.从外向内为白色、黑色、蓝色、红色,靶心是金色,金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,靶心直径为12.2cm.运动员在70m外射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率是多少
射中靶面直径为122cm的大圆内的任意一点.
这两个问题能否用古典概型的方法来求解呢
怎么办呢
基本事件:
问题情境
下图是卧室和书房地板的示意图,图中每一块方砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,并随意停留在某块方砖上。在哪个房间里,小猫停留在黑砖上的概率大?
卧 室
书 房
创设情境3:
问题情境3
对于问题1.记“剪得两段绳长都不小于10cm”为事件A. 把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生.由于中间一段的长度等于绳长的1/3.
对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中的每一个点被取到的机会都一样,而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点.这里的区域可以是线段、平面图形、立体图形等.用这种方法处理随机试验,称为几何概型.
几何概型的特点:
(1)基本事件有无限多个;
(2)基本事件发生是等可能的.
构建数学
一般地,在几何区域D中随机地取一点,记“该点落在其内部一个区域d内”为事件A,则事件A发生的概率:
注:
(2)D的测度不为0,当D分别是线段、平面图形、立体图形时,相应的“测度”分别是长度、面积和体积.
(1)古典概型与几何概型的区别在于:
几何概型是无限多个等可能事件的情况,
而古典概型中的等可能事件只有有限多个;
(3)在区域D内随机取点是指:该点落在D内任何一处都是等可能的,落在任何部分的可能性只与该部分的测度成正比而与其性状位置无关.
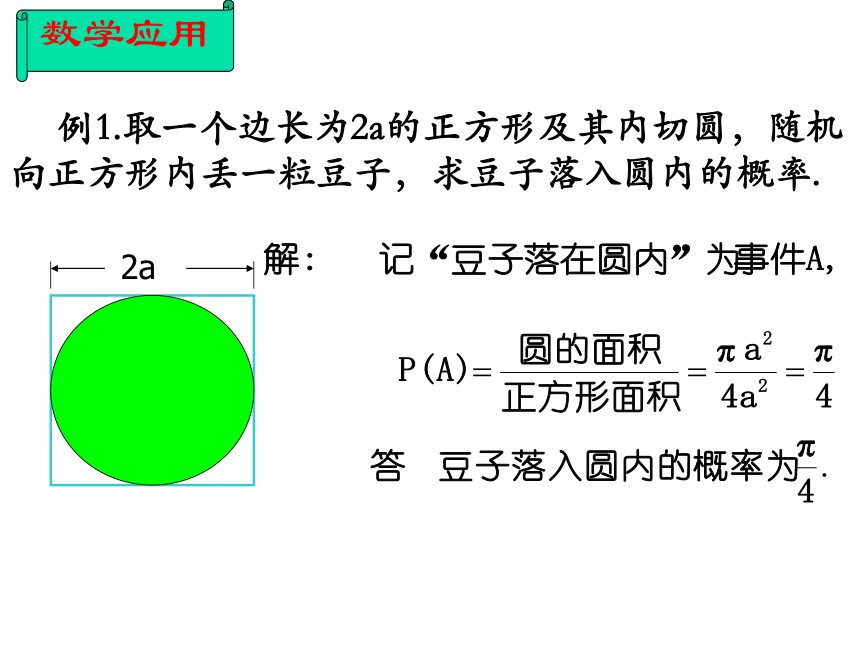
例1.取一个边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.
2a
数学应用
数学应用
数学拓展:模拟撒豆子试验估计圆周率
由此可得
如果向正方形内撒 颗豆子,其中落在圆内的
豆子数为 ,那么当 很大时,比值 ,
即频率应接近与 ,于是有
例2.两根相距8m的木杆上系一根拉直绳子,并在绳子上挂一盏灯,求灯与两端距离都大于3m的概率.
数学应用
解:记“灯与两端距离都大于3m”为事件A,
由于绳长8m,当挂灯位置介于中间2m
时,事件A发生,于是
1.某人午休醒来,发觉表停了,他打开收音机想听电台整点报时,求他等待的时间短于10分钟的概率.
2.已知地铁列车每10min一班,在车站停1min.求乘客到达站台立即乘上车的概率.
打开收音机的时刻位于[50,60]时间段内则事件A发生.
由几何概型的求概率公式得
P(A)=(60-50)/60=1/6
即“等待报时的时间不超过10分钟”的概率为1/6.
练一练:
解:记“等待的时间小于10分钟”为事件A,
3.在1万平方公里的海域中有40平方公里的大陆贮
藏着石油.假如在海域中任意一点钻探,钻到油层面
的概率是多少
练一练:
4.如右下图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到阴影部分的概率.
课堂小结
1.古典概型与几何概型的区别.
相同:两者基本事件的发生都是等可能的;
不同:古典概型要求基本事件有有限个,
几何概型要求基本事件有无限多个.
2.几何概型的概率公式.
3.几何概型问题的概率的求解.
例3.在1L高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10mL,含有麦锈病种子的概率是多少
5.有一杯1升的水,其中含有1个大肠杆菌,
用一个小杯从这杯水中取出0.1升,求小
杯水中含有这个细菌的概率.
练一练:
1.国家安全机关监听录音机记录了两个间谍的谈话, 发现30min的磁带上,从开始30s处起,有10s长的一段内容包含间谍犯罪的 信息.后来发现,这段谈话的部分被某工作人员擦掉了,该工作人员声称他完全是无意中按错了键,使从此后起往后的所有内容都被擦掉了.那么由于按错了键使含有犯罪内容的谈话被部分或全部
擦掉的概率有多大?
思 考:
解:记事件A:按错键使含有犯罪内容的谈话被部分或全部擦掉.则事件A发生就是在0--2/3min时间段内按错键.故
P(A)=
2
3
30
=
1
45
2.(会面问题)甲、乙二人约定在 12 点到 5 点之间在某地会面,先到者等一个小时后即离去,设二人在这段时间内的各时刻到达是等可能的,且二人互不影响。求二人能会面的概率。
解: 以 X , Y 分别表示甲、乙二人到达的时刻,于是
即 点 M 落在图中的阴影部
分.所有的点构成一个正
方形,即有无穷多个结果.
由于每人在任一时刻到达
都是等可能的,所以落在正
方形内各点是等可能的.
.M(X,Y)
y
5
4
3
2
1
0 1 2 3 4 5
x
二人会面的条件是:
0 1 2 3 4 5
y
x
5
4
3
2
1
y=x+1
y=x -1
记“两人会面”为事件A
练习: 假设你家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00—8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少
解:
以横坐标X表示报纸送到时间,以纵
坐标Y表示父亲离家时间建立平面
直角坐标系,由于随机试验落在方
形区域内任何一点是等可能的,所
以符合几何概型的条件.根据题意,
只要点落到阴影部分,就表示父亲
在离开家前能得到报纸,即时间A
发生,所以
Good bye……
作业:P103习题3.3
ex 2.3.4
2、危害。小麦感病后,由于养料被病菌夺取,
叶绿素遭受破坏,光合作用面积减少,叶片表皮破裂,
水分蒸腾量增加,呼吸作用加强,至使麦株生长发育受阻。
感病轻的,麦粒不饱满,影响产量,出粉率差;感病重的,
麦粒不能灌浆,造成大幅度减产。
1964年4—5月间,小麦锈病在全国麦区流行,华北、西北冬麦区大流行。据统计,全国发生面积800万公顷,损失小麦约32亿公斤。
发病大都以条锈病为主,发病后蔓延快,危害重. 小麦感病后,由于养料被病菌夺取,叶绿素遭受破坏,光合作用面积减少,叶片表皮破裂,水分蒸腾量增加,呼吸作用加强,至使麦株生长发育受阻。感病轻的,麦粒不饱满,影响产量,出粉率差;感病重的,麦粒不能灌浆,造成大幅度减产。
麦锈病的危害
(第一课时)
复习
古典概型的两个基本特点:
(1)所有的基本事件只有有限个;
(2)每个基本事件发生都是等可能的.
那么对于有无限多个试验结果的情况相应的概率应如果求呢
1.取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?
从30cm的绳子上的任意一点剪断.
基本事件:
问题情境
2.射箭比赛的箭靶是涂有五个彩色的分环.从外向内为白色、黑色、蓝色、红色,靶心是金色,金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,靶心直径为12.2cm.运动员在70m外射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率是多少
射中靶面直径为122cm的大圆内的任意一点.
这两个问题能否用古典概型的方法来求解呢
怎么办呢
基本事件:
问题情境
下图是卧室和书房地板的示意图,图中每一块方砖除颜色外完全相同,小猫分别在卧室和书房中自由地走来走去,并随意停留在某块方砖上。在哪个房间里,小猫停留在黑砖上的概率大?
卧 室
书 房
创设情境3:
问题情境3
对于问题1.记“剪得两段绳长都不小于10cm”为事件A. 把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生.由于中间一段的长度等于绳长的1/3.
对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中的每一个点被取到的机会都一样,而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点.这里的区域可以是线段、平面图形、立体图形等.用这种方法处理随机试验,称为几何概型.
几何概型的特点:
(1)基本事件有无限多个;
(2)基本事件发生是等可能的.
构建数学
一般地,在几何区域D中随机地取一点,记“该点落在其内部一个区域d内”为事件A,则事件A发生的概率:
注:
(2)D的测度不为0,当D分别是线段、平面图形、立体图形时,相应的“测度”分别是长度、面积和体积.
(1)古典概型与几何概型的区别在于:
几何概型是无限多个等可能事件的情况,
而古典概型中的等可能事件只有有限多个;
(3)在区域D内随机取点是指:该点落在D内任何一处都是等可能的,落在任何部分的可能性只与该部分的测度成正比而与其性状位置无关.
例1.取一个边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.
2a
数学应用
数学应用
数学拓展:模拟撒豆子试验估计圆周率
由此可得
如果向正方形内撒 颗豆子,其中落在圆内的
豆子数为 ,那么当 很大时,比值 ,
即频率应接近与 ,于是有
例2.两根相距8m的木杆上系一根拉直绳子,并在绳子上挂一盏灯,求灯与两端距离都大于3m的概率.
数学应用
解:记“灯与两端距离都大于3m”为事件A,
由于绳长8m,当挂灯位置介于中间2m
时,事件A发生,于是
1.某人午休醒来,发觉表停了,他打开收音机想听电台整点报时,求他等待的时间短于10分钟的概率.
2.已知地铁列车每10min一班,在车站停1min.求乘客到达站台立即乘上车的概率.
打开收音机的时刻位于[50,60]时间段内则事件A发生.
由几何概型的求概率公式得
P(A)=(60-50)/60=1/6
即“等待报时的时间不超过10分钟”的概率为1/6.
练一练:
解:记“等待的时间小于10分钟”为事件A,
3.在1万平方公里的海域中有40平方公里的大陆贮
藏着石油.假如在海域中任意一点钻探,钻到油层面
的概率是多少
练一练:
4.如右下图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到阴影部分的概率.
课堂小结
1.古典概型与几何概型的区别.
相同:两者基本事件的发生都是等可能的;
不同:古典概型要求基本事件有有限个,
几何概型要求基本事件有无限多个.
2.几何概型的概率公式.
3.几何概型问题的概率的求解.
例3.在1L高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10mL,含有麦锈病种子的概率是多少
5.有一杯1升的水,其中含有1个大肠杆菌,
用一个小杯从这杯水中取出0.1升,求小
杯水中含有这个细菌的概率.
练一练:
1.国家安全机关监听录音机记录了两个间谍的谈话, 发现30min的磁带上,从开始30s处起,有10s长的一段内容包含间谍犯罪的 信息.后来发现,这段谈话的部分被某工作人员擦掉了,该工作人员声称他完全是无意中按错了键,使从此后起往后的所有内容都被擦掉了.那么由于按错了键使含有犯罪内容的谈话被部分或全部
擦掉的概率有多大?
思 考:
解:记事件A:按错键使含有犯罪内容的谈话被部分或全部擦掉.则事件A发生就是在0--2/3min时间段内按错键.故
P(A)=
2
3
30
=
1
45
2.(会面问题)甲、乙二人约定在 12 点到 5 点之间在某地会面,先到者等一个小时后即离去,设二人在这段时间内的各时刻到达是等可能的,且二人互不影响。求二人能会面的概率。
解: 以 X , Y 分别表示甲、乙二人到达的时刻,于是
即 点 M 落在图中的阴影部
分.所有的点构成一个正
方形,即有无穷多个结果.
由于每人在任一时刻到达
都是等可能的,所以落在正
方形内各点是等可能的.
.M(X,Y)
y
5
4
3
2
1
0 1 2 3 4 5
x
二人会面的条件是:
0 1 2 3 4 5
y
x
5
4
3
2
1
y=x+1
y=x -1
记“两人会面”为事件A
练习: 假设你家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00—8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少
解:
以横坐标X表示报纸送到时间,以纵
坐标Y表示父亲离家时间建立平面
直角坐标系,由于随机试验落在方
形区域内任何一点是等可能的,所
以符合几何概型的条件.根据题意,
只要点落到阴影部分,就表示父亲
在离开家前能得到报纸,即时间A
发生,所以
Good bye……
作业:P103习题3.3
ex 2.3.4
2、危害。小麦感病后,由于养料被病菌夺取,
叶绿素遭受破坏,光合作用面积减少,叶片表皮破裂,
水分蒸腾量增加,呼吸作用加强,至使麦株生长发育受阻。
感病轻的,麦粒不饱满,影响产量,出粉率差;感病重的,
麦粒不能灌浆,造成大幅度减产。
1964年4—5月间,小麦锈病在全国麦区流行,华北、西北冬麦区大流行。据统计,全国发生面积800万公顷,损失小麦约32亿公斤。
发病大都以条锈病为主,发病后蔓延快,危害重. 小麦感病后,由于养料被病菌夺取,叶绿素遭受破坏,光合作用面积减少,叶片表皮破裂,水分蒸腾量增加,呼吸作用加强,至使麦株生长发育受阻。感病轻的,麦粒不饱满,影响产量,出粉率差;感病重的,麦粒不能灌浆,造成大幅度减产。
麦锈病的危害
同课章节目录
