概率加法公式4
图片预览

文档简介
(共15张PPT)
3.1.4 概率的加法公式
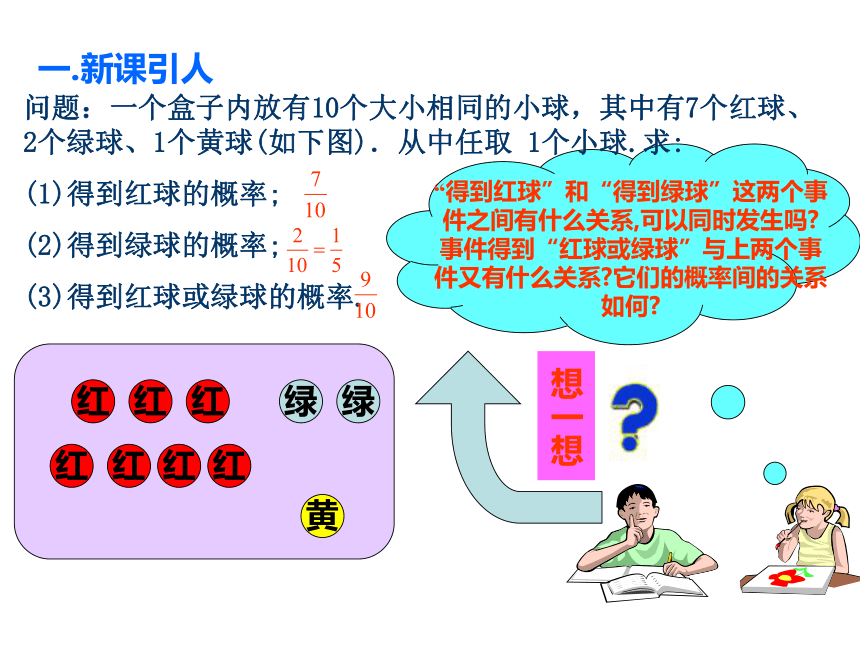
问题:一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、1个黄球(如下图).从中任取 1个小球.求:
(1)得到红球的概率;
(2)得到绿球的概率;
(3)得到红球或绿球的概率.
一.新课引人
红
绿
黄
绿
红
红
红
红
红
红
“得到红球”和“得到绿球”这两个事件之间有什么关系,可以同时发生吗 事件得到“红球或绿球”与上两个事件又有什么关系 它们的概率间的关系如何
想一想
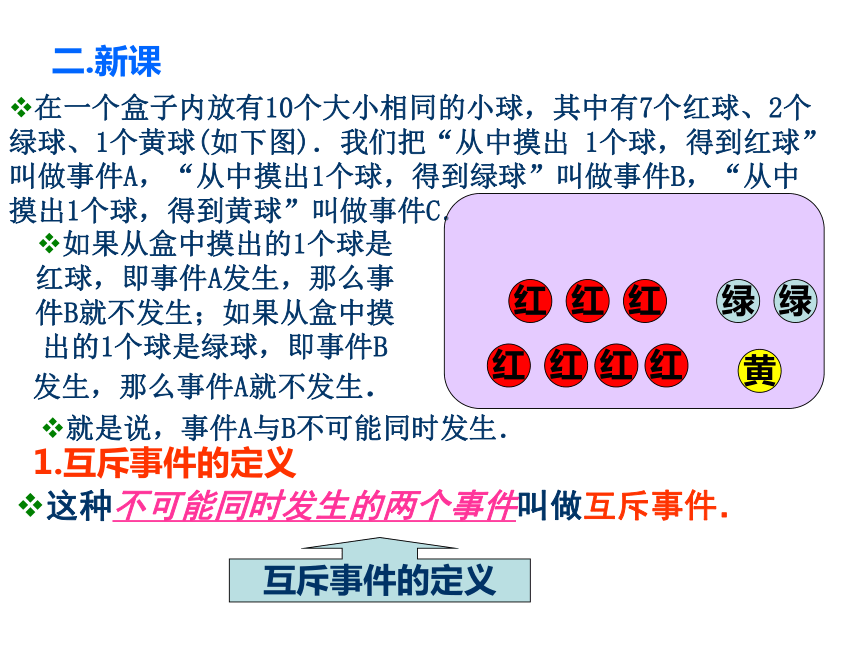
在一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、1个黄球(如下图).我们把“从中摸出 1个球,得到红球”叫做事件A,“从中摸出1个球,得到绿球”叫做事件B,“从中摸出1个球,得到黄球”叫做事件C.
二.新课
红
绿
黄
绿
红
红
红
红
红
红
如果从盒中摸出的1个球是红球,即事件A发生,那么事件B就不发生;如果从盒中摸出的1个球是绿球,即事件B发生,那么事件A就不发生.
就是说,事件A与B不可能同时发生.
这种不可能同时发生的两个事件叫做互斥事件.
互斥事件的定义
1.互斥事件的定义
红
绿
绿
红
红
红
红
红
红
C
黄
A
B
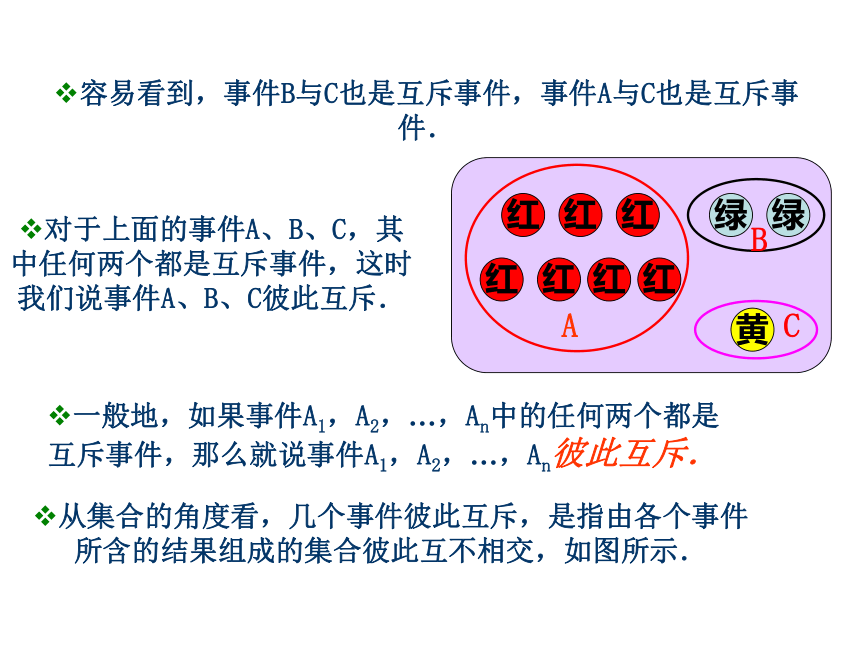
对于上面的事件A、B、C,其中任何两个都是互斥事件,这时我们说事件A、B、C彼此互斥.
一般地,如果事件A1,A2,…,An中的任何两个都是互斥事件,那么就说事件A1,A2,…,An彼此互斥.
从集合的角度看,几个事件彼此互斥,是指由各个事件所含的结果组成的集合彼此互不相交,如图所示.
容易看到,事件B与C也是互斥事件,事件A与C也是互斥事件.
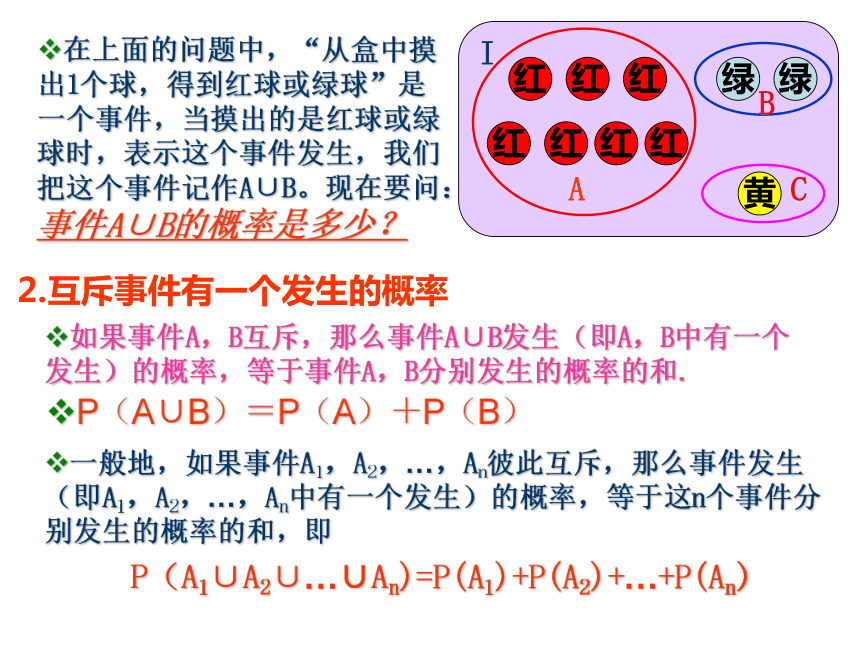
在上面的问题中,“从盒中摸出1个球,得到红球或绿球”是一个事件,当摸出的是红球或绿球时,表示这个事件发生,我们把这个事件记作A∪B。现在要问:事件A∪B的概率是多少?
I
红
红
红
红
红
红
红
A
绿
绿
C
黄
B
一般地,如果事件A1,A2,…,An彼此互斥,那么事件发生(即A1,A2,…,An中有一个发生)的概率,等于这n个事件分别发生的概率的和,即
P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An)
P(A∪B)=P(A)+P(B)
如果事件A,B互斥,那么事件A∪B发生(即A,B中有一个发生)的概率,等于事件A,B分别发生的概率的和.
2.互斥事件有一个发生的概率
I
“从盒中摸出1个球,得到的不是红球(即绿球或黄球)”记作事件
.
红
红
红
红
红
红
红
A
绿
绿
C
黄
B
红
红
红
红
红
红
红
A
绿
绿
C
黄
B
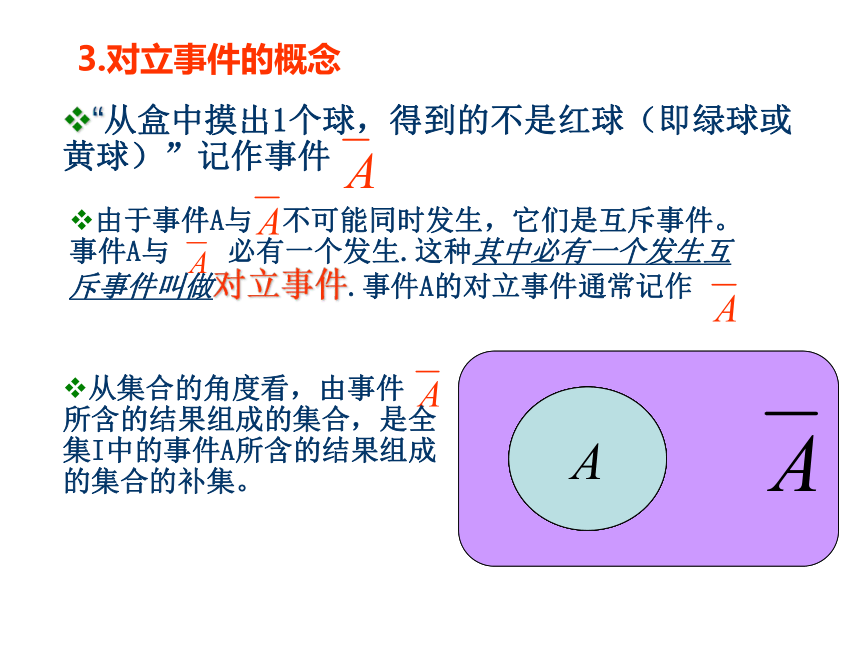
3.对立事件的概念
由于事件A与 不可能同时发生,它们是互斥事件。事件A与 必有一个发生.这种其中必有一个发生互斥事件叫做对立事件.事件A的对立事件通常记作
从集合的角度看,由事件 所含的结果组成的集合,是全集I中的事件A所含的结果组成的集合的补集。
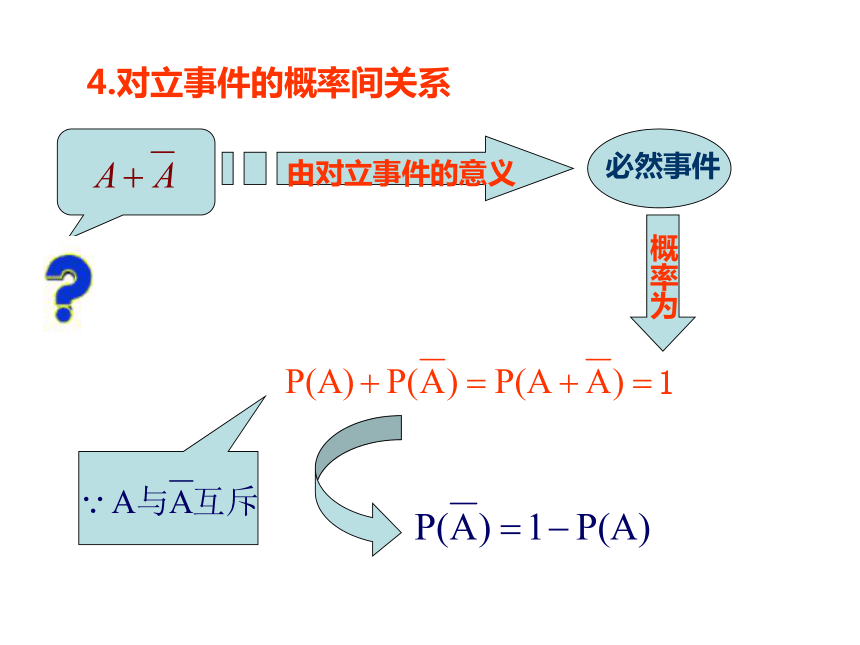
4.对立事件的概率间关系
必然事件
由对立事件的意义
概率为
1
互斥事件及对立事件的概念
互斥事件概念:不能同时发生的两个事件称为互斥事件
如果事件A1,A2,…,An中的任何两个都是互斥事件,就说事件A1,A2,…,An彼此互斥
设A,B为互斥事件,当事件A,B 有一个发生,我们把这个事件记作A+B。
对立事件概念:两个互斥事必有一个发生,则称这两个事件为对立事件。事件A的对立事件记为
A
对立事件是互斥事件,
互斥事件不一定是对立事件。
互斥事件概念:不能同时发生的两个事件称为互斥事件
如果事件A1,A2,…,An中的任何两个都是互斥事件,就说事件A1,A2,…,An彼此互斥
设A,B为互斥事件,当事件A,B 有一个发生,我们把这个事件记作A∪B。
对立事件概念:两个互斥事必有一个发生,则称这两个事件为对立事件。事件A的对立事件记为
思考:互斥事件与对立事件有何关系?
练习1:体育考试的成绩分为四个等级:优,良,中,不及格, 某班50名学生参加了体育考试,结果如下:
优 85分及以上 9人
良 75~84分 15人
中 60~74分 21人
不及格 60分以下 5人
2、从这个班任意抽取一位同学,那么这位同学的体育成绩为“优良”
(优或良)的概率是多少
1、体育考试的成绩的等级为优 良 中 不及格的事件分别记为A,B,C,D,
它们相互之间有何关系?分别求出它们的概率。
3、记“优良” (优或良)为事件E,记“中差” (中或不及格)为事件F,事件E与为事件F之间有何关系?它们的概率之间又有何关系?
例1
一只口袋内装有大小一样的4只白球和4只
黑球,从中任意摸出2只球。记摸出2只白球的事件为A,摸出1只白球和1只黑球的事件为B.问:事件A与事件B是否为互斥事件?是否为对立事件?
解:因为事件A与事件B是不能同时发生,所以是互斥事件;
因为从中一次可以摸出2只黑球,所以事件A与事件B
不是对立事件。
例2.某人射击一次,命中7-10环的概率如下图
所示:
(1)求射击1次,至少命中7环的概率;
(2)求射击1次命中不足7环的概率。
7环
命中环数
概率
10环
9环
8环
0.12
0.18
0.28
0.32
练习2 某地区的年降水量在下列范围内的概率如下所示:
年降水量(单位:mm) [100,150) [150,200) [200,250) [250,300)
概率 0.12 0.25 0.16 0.14
1.求年降水量在[100,200)(㎜)范围内的概率;
2.求年降水量在[150,300)(mm)范围内的概率。
解:(1)记这个地区的年降水量在[100,150),[150,200),[200,250),[250,300)(mm)范围内分别为事件为A、B、C、D。
这4个事件是彼此互斥的。根据互斥事件的概率加法公式,有
(1)年降水量在[100,200)(mm)范围内的概率是
P(A∪B)=P(A)+P(B)=0.12+0.25=0.37
答:……
(2)年降水量在[150,300)(mm)内的概率是
P(B∪C∪D)=P(B)+P(C)+P(D)=0.25+0.16+0.14=0.55.
答:……
例3.黄种人群中各种血型的人所占的比如下表所示:
血型
所占比例
A
B
AB
28
29
8
O
35
已知同种血型的人可以输血,O型血可以输给任何一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血
(1)求任找一人,其血可以输给小明的概率;
(2)求任找一人,其血不能输给小明的概率。
互斥事件:不可能同时发生的两个事件。当A、B是互斥事件时,P(A∪B)=P(A)+P(B)
对立事件:其中必有一个发生的两个互斥事件叫做对立事件。当A、B是对立事件时,P(B)=1-P(A)
课堂小结
3.1.4 概率的加法公式
问题:一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、1个黄球(如下图).从中任取 1个小球.求:
(1)得到红球的概率;
(2)得到绿球的概率;
(3)得到红球或绿球的概率.
一.新课引人
红
绿
黄
绿
红
红
红
红
红
红
“得到红球”和“得到绿球”这两个事件之间有什么关系,可以同时发生吗 事件得到“红球或绿球”与上两个事件又有什么关系 它们的概率间的关系如何
想一想
在一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、1个黄球(如下图).我们把“从中摸出 1个球,得到红球”叫做事件A,“从中摸出1个球,得到绿球”叫做事件B,“从中摸出1个球,得到黄球”叫做事件C.
二.新课
红
绿
黄
绿
红
红
红
红
红
红
如果从盒中摸出的1个球是红球,即事件A发生,那么事件B就不发生;如果从盒中摸出的1个球是绿球,即事件B发生,那么事件A就不发生.
就是说,事件A与B不可能同时发生.
这种不可能同时发生的两个事件叫做互斥事件.
互斥事件的定义
1.互斥事件的定义
红
绿
绿
红
红
红
红
红
红
C
黄
A
B
对于上面的事件A、B、C,其中任何两个都是互斥事件,这时我们说事件A、B、C彼此互斥.
一般地,如果事件A1,A2,…,An中的任何两个都是互斥事件,那么就说事件A1,A2,…,An彼此互斥.
从集合的角度看,几个事件彼此互斥,是指由各个事件所含的结果组成的集合彼此互不相交,如图所示.
容易看到,事件B与C也是互斥事件,事件A与C也是互斥事件.
在上面的问题中,“从盒中摸出1个球,得到红球或绿球”是一个事件,当摸出的是红球或绿球时,表示这个事件发生,我们把这个事件记作A∪B。现在要问:事件A∪B的概率是多少?
I
红
红
红
红
红
红
红
A
绿
绿
C
黄
B
一般地,如果事件A1,A2,…,An彼此互斥,那么事件发生(即A1,A2,…,An中有一个发生)的概率,等于这n个事件分别发生的概率的和,即
P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An)
P(A∪B)=P(A)+P(B)
如果事件A,B互斥,那么事件A∪B发生(即A,B中有一个发生)的概率,等于事件A,B分别发生的概率的和.
2.互斥事件有一个发生的概率
I
“从盒中摸出1个球,得到的不是红球(即绿球或黄球)”记作事件
.
红
红
红
红
红
红
红
A
绿
绿
C
黄
B
红
红
红
红
红
红
红
A
绿
绿
C
黄
B
3.对立事件的概念
由于事件A与 不可能同时发生,它们是互斥事件。事件A与 必有一个发生.这种其中必有一个发生互斥事件叫做对立事件.事件A的对立事件通常记作
从集合的角度看,由事件 所含的结果组成的集合,是全集I中的事件A所含的结果组成的集合的补集。
4.对立事件的概率间关系
必然事件
由对立事件的意义
概率为
1
互斥事件及对立事件的概念
互斥事件概念:不能同时发生的两个事件称为互斥事件
如果事件A1,A2,…,An中的任何两个都是互斥事件,就说事件A1,A2,…,An彼此互斥
设A,B为互斥事件,当事件A,B 有一个发生,我们把这个事件记作A+B。
对立事件概念:两个互斥事必有一个发生,则称这两个事件为对立事件。事件A的对立事件记为
A
对立事件是互斥事件,
互斥事件不一定是对立事件。
互斥事件概念:不能同时发生的两个事件称为互斥事件
如果事件A1,A2,…,An中的任何两个都是互斥事件,就说事件A1,A2,…,An彼此互斥
设A,B为互斥事件,当事件A,B 有一个发生,我们把这个事件记作A∪B。
对立事件概念:两个互斥事必有一个发生,则称这两个事件为对立事件。事件A的对立事件记为
思考:互斥事件与对立事件有何关系?
练习1:体育考试的成绩分为四个等级:优,良,中,不及格, 某班50名学生参加了体育考试,结果如下:
优 85分及以上 9人
良 75~84分 15人
中 60~74分 21人
不及格 60分以下 5人
2、从这个班任意抽取一位同学,那么这位同学的体育成绩为“优良”
(优或良)的概率是多少
1、体育考试的成绩的等级为优 良 中 不及格的事件分别记为A,B,C,D,
它们相互之间有何关系?分别求出它们的概率。
3、记“优良” (优或良)为事件E,记“中差” (中或不及格)为事件F,事件E与为事件F之间有何关系?它们的概率之间又有何关系?
例1
一只口袋内装有大小一样的4只白球和4只
黑球,从中任意摸出2只球。记摸出2只白球的事件为A,摸出1只白球和1只黑球的事件为B.问:事件A与事件B是否为互斥事件?是否为对立事件?
解:因为事件A与事件B是不能同时发生,所以是互斥事件;
因为从中一次可以摸出2只黑球,所以事件A与事件B
不是对立事件。
例2.某人射击一次,命中7-10环的概率如下图
所示:
(1)求射击1次,至少命中7环的概率;
(2)求射击1次命中不足7环的概率。
7环
命中环数
概率
10环
9环
8环
0.12
0.18
0.28
0.32
练习2 某地区的年降水量在下列范围内的概率如下所示:
年降水量(单位:mm) [100,150) [150,200) [200,250) [250,300)
概率 0.12 0.25 0.16 0.14
1.求年降水量在[100,200)(㎜)范围内的概率;
2.求年降水量在[150,300)(mm)范围内的概率。
解:(1)记这个地区的年降水量在[100,150),[150,200),[200,250),[250,300)(mm)范围内分别为事件为A、B、C、D。
这4个事件是彼此互斥的。根据互斥事件的概率加法公式,有
(1)年降水量在[100,200)(mm)范围内的概率是
P(A∪B)=P(A)+P(B)=0.12+0.25=0.37
答:……
(2)年降水量在[150,300)(mm)内的概率是
P(B∪C∪D)=P(B)+P(C)+P(D)=0.25+0.16+0.14=0.55.
答:……
例3.黄种人群中各种血型的人所占的比如下表所示:
血型
所占比例
A
B
AB
28
29
8
O
35
已知同种血型的人可以输血,O型血可以输给任何一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血
(1)求任找一人,其血可以输给小明的概率;
(2)求任找一人,其血不能输给小明的概率。
互斥事件:不可能同时发生的两个事件。当A、B是互斥事件时,P(A∪B)=P(A)+P(B)
对立事件:其中必有一个发生的两个互斥事件叫做对立事件。当A、B是对立事件时,P(B)=1-P(A)
课堂小结
同课章节目录
