湘教版初中数学九年级下册 1.2.3 二次函数y=a(x-h)2的图象与性质 教案(表格式)
文档属性
| 名称 | 湘教版初中数学九年级下册 1.2.3 二次函数y=a(x-h)2的图象与性质 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 289.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 00:00:00 | ||
图片预览


文档简介
学校名称
课例名称
二次函数的
图象与性质
教师姓名
学段学科
初中数学
教材版本
章节
年级
九年级下
教学目标
1.会用描点法画函数图象,理解抛物线
与
?图象之间的位置关系。
2.体验抛物线的平移过程,形成良好的思维方法。
3.在探究过程中,让学生体验成功的快乐,进一步培养学生学习数学的兴趣。
4.在探究函数图象平移规律的过程,继续渗透数形结合的思想方法。
教学重难点
重点:会画二次函数的图象,掌握函数性质。
难点:抛物线通过平移后得到时,确定平移的方向和距离。
学情分析
从认知状况来说,之前已经对函数已经有了初步的认识,在教学过程中,引导学生自主学习。
从心理特征来说,学生进入九年级之后,课堂气氛比较沉闷,不爱发言,在教学过程中,我设计了小组讨论环节,激发学生学习的主动性。
教学方法
本节教学分探究,讨论,归纳,运用四个层次,侧重学生自主学习,由旧知识类比得出新知识。
为了更好地掌握重点,突破难点,本节课运用了Excel绘制表格,希沃同屏助手及动画演示等信息技术手段。
教学过程
一
新课导入:
二
问题探究:
探究1:
通过学生动手画函数图象,让学生经历知识的发生,发展过程。
利用Excel绘制表格,为学生提供网格直角坐标系,这样可以节省画图时间,提高学生所画抛物线位置的准确性,使学生更容易看出抛物线平移的距离。
通过希沃同屏助手,展示学生所画的函数图象,进行及时纠错,为学生顺利进入新知识做好准备。
通过教师课件的演示,让学生能更直观地,认识到两函数图象的位置关系。
思考:函数能否由?直接平移得到?
课件演示,观察表达式,x+1
变成
x-2,应该-3,向右平移3个单位长度。
练习1:
总结平移规律
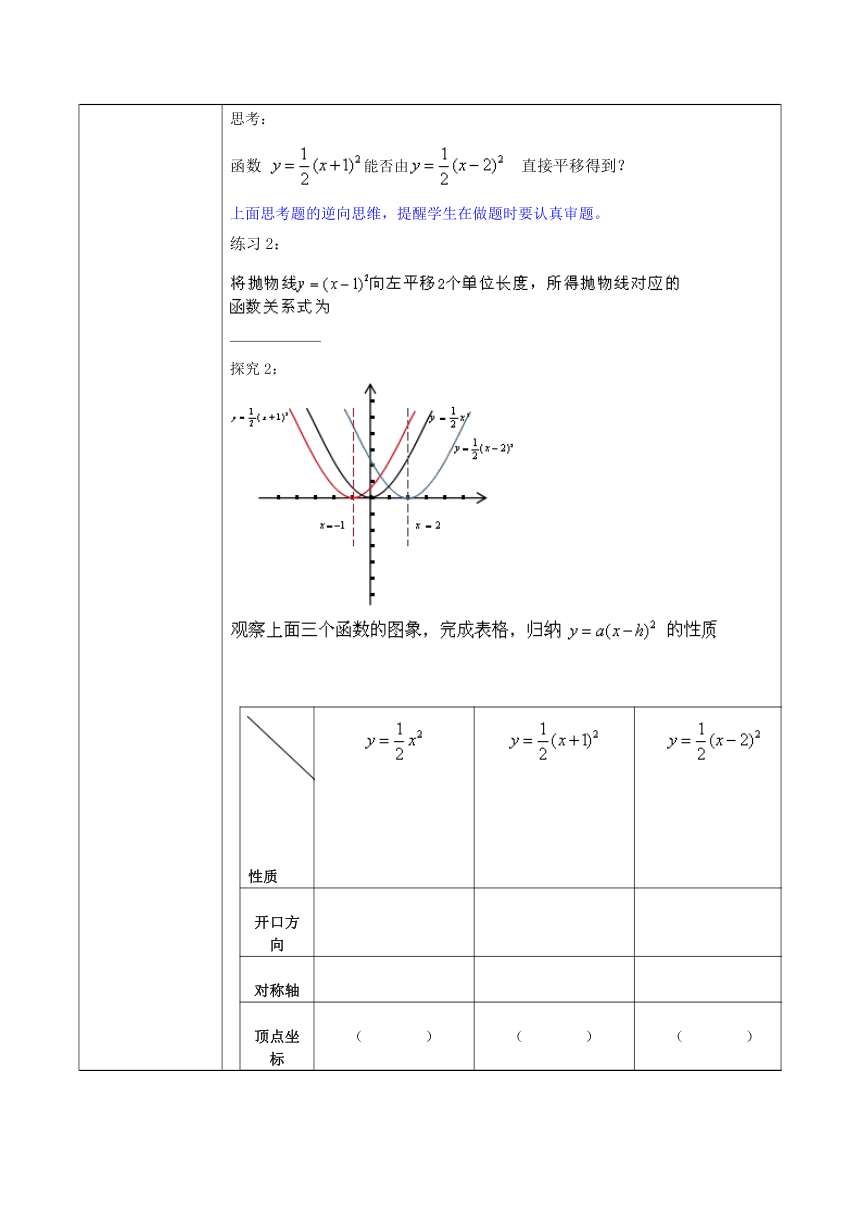
思考:
函数能否由?直接平移得到?
上面思考题的逆向思维,提醒学生在做题时要认真审题。
练习2:
探究2:
?
?
性质
开口方向
对称轴
顶点坐标
(
)
(
)
(
)
函数值的变化情况当x
时,
y随x的增大而减小当x
时,
y随x的增大而减小当x
时,
y随x的增大而减小当x
时,
y随x的增大而增大当x
时,
y随x的增大而增大当x
时,
y随x的增大而增大
最值函数图象有最
点,
当x
=
时,
函数有最
值,
值为
函数图象有最
点,
当x
=
时,
函数有最
值,
值为
函数图象有最
点,
当x
=
时,
函数有最
值,
值为
练习3:
1.
抛物线y=5(x-2)?的顶点坐标是(
)
A.(-2,0)
B.(2,0)
C.(0,-2)
D.(0,2)
2.
(中考·兰州)在下列二次函数中,其图象的对称轴为直线
x=-2
的是(
)
A.y=(x+2)?
B.y=2x?-2
C.y=-2x?-2
D.y=2(x-2)?
3.
抛物线
y=9(x+12)?-3
开口向______,
对称轴是
__________,
顶点坐标是_____
___;
当
x______时,y
随
x
的增大而增大;
当
x=________时,y
有最
________值,这个值为________.
探究3:
小组讨论归纳二次函数性质:
通过小组讨论,引导学生完成对知识从特殊到一般的归纳,从而培养学生分析问题和解决问题的能力。
练习4:
1.
关于函数y=-2(x+3)?,下列说法正确的是(
)
A.其图象的开口向上
B.其图象的对称轴是直线x=3
C.其图象的顶点坐标是(0,3)
D.当x>-3时,y随x的增大而减小
2.
已知抛物线
y=-(x+1)?上的两点A(x?,y?),B(x?,
y?),若
x?<x?<-1,则下列结论成立的是(
)
A.y?<y?<0
B.0<y?<y?
C.0<y?<y?
D.y?<y?<0
3.
已知抛物线
y=a(x-h)?
的形状及开口方向与抛物线
y=-2x?相同,且顶点坐标为(-2,0),则
a+h=
课堂小结:
教学反思
本节课主要是借助多媒体,动态的展示了二次函数的平移过程,让学生自己总结规律,很形象,便于记忆。
但在教学中,我自认为热情不够,没有积极调动学生学习热情的语言,感染力不足。今后备课时要重视创设丰富而风趣的语言,来调动学生的积极性。
总之,在数学教学中不但要善于设疑置难,而且要理论联系实际,只有这样,才会吸引学生对数学学科的热爱。
课例名称
二次函数的
图象与性质
教师姓名
学段学科
初中数学
教材版本
章节
年级
九年级下
教学目标
1.会用描点法画函数图象,理解抛物线
与
?图象之间的位置关系。
2.体验抛物线的平移过程,形成良好的思维方法。
3.在探究过程中,让学生体验成功的快乐,进一步培养学生学习数学的兴趣。
4.在探究函数图象平移规律的过程,继续渗透数形结合的思想方法。
教学重难点
重点:会画二次函数的图象,掌握函数性质。
难点:抛物线通过平移后得到时,确定平移的方向和距离。
学情分析
从认知状况来说,之前已经对函数已经有了初步的认识,在教学过程中,引导学生自主学习。
从心理特征来说,学生进入九年级之后,课堂气氛比较沉闷,不爱发言,在教学过程中,我设计了小组讨论环节,激发学生学习的主动性。
教学方法
本节教学分探究,讨论,归纳,运用四个层次,侧重学生自主学习,由旧知识类比得出新知识。
为了更好地掌握重点,突破难点,本节课运用了Excel绘制表格,希沃同屏助手及动画演示等信息技术手段。
教学过程
一
新课导入:
二
问题探究:
探究1:
通过学生动手画函数图象,让学生经历知识的发生,发展过程。
利用Excel绘制表格,为学生提供网格直角坐标系,这样可以节省画图时间,提高学生所画抛物线位置的准确性,使学生更容易看出抛物线平移的距离。
通过希沃同屏助手,展示学生所画的函数图象,进行及时纠错,为学生顺利进入新知识做好准备。
通过教师课件的演示,让学生能更直观地,认识到两函数图象的位置关系。
思考:函数能否由?直接平移得到?
课件演示,观察表达式,x+1
变成
x-2,应该-3,向右平移3个单位长度。
练习1:
总结平移规律
思考:
函数能否由?直接平移得到?
上面思考题的逆向思维,提醒学生在做题时要认真审题。
练习2:
探究2:
?
?
性质
开口方向
对称轴
顶点坐标
(
)
(
)
(
)
函数值的变化情况当x
时,
y随x的增大而减小当x
时,
y随x的增大而减小当x
时,
y随x的增大而减小当x
时,
y随x的增大而增大当x
时,
y随x的增大而增大当x
时,
y随x的增大而增大
最值函数图象有最
点,
当x
=
时,
函数有最
值,
值为
函数图象有最
点,
当x
=
时,
函数有最
值,
值为
函数图象有最
点,
当x
=
时,
函数有最
值,
值为
练习3:
1.
抛物线y=5(x-2)?的顶点坐标是(
)
A.(-2,0)
B.(2,0)
C.(0,-2)
D.(0,2)
2.
(中考·兰州)在下列二次函数中,其图象的对称轴为直线
x=-2
的是(
)
A.y=(x+2)?
B.y=2x?-2
C.y=-2x?-2
D.y=2(x-2)?
3.
抛物线
y=9(x+12)?-3
开口向______,
对称轴是
__________,
顶点坐标是_____
___;
当
x______时,y
随
x
的增大而增大;
当
x=________时,y
有最
________值,这个值为________.
探究3:
小组讨论归纳二次函数性质:
通过小组讨论,引导学生完成对知识从特殊到一般的归纳,从而培养学生分析问题和解决问题的能力。
练习4:
1.
关于函数y=-2(x+3)?,下列说法正确的是(
)
A.其图象的开口向上
B.其图象的对称轴是直线x=3
C.其图象的顶点坐标是(0,3)
D.当x>-3时,y随x的增大而减小
2.
已知抛物线
y=-(x+1)?上的两点A(x?,y?),B(x?,
y?),若
x?<x?<-1,则下列结论成立的是(
)
A.y?<y?<0
B.0<y?<y?
C.0<y?<y?
D.y?<y?<0
3.
已知抛物线
y=a(x-h)?
的形状及开口方向与抛物线
y=-2x?相同,且顶点坐标为(-2,0),则
a+h=
课堂小结:
教学反思
本节课主要是借助多媒体,动态的展示了二次函数的平移过程,让学生自己总结规律,很形象,便于记忆。
但在教学中,我自认为热情不够,没有积极调动学生学习热情的语言,感染力不足。今后备课时要重视创设丰富而风趣的语言,来调动学生的积极性。
总之,在数学教学中不但要善于设疑置难,而且要理论联系实际,只有这样,才会吸引学生对数学学科的热爱。
