Unit 1 Great scientists-Reading task
文档属性
| 名称 | Unit 1 Great scientists-Reading task |  | |
| 格式 | rar | ||
| 文件大小 | 310.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 英语 | ||
| 更新时间 | 2011-12-09 19:38:13 | ||
图片预览







文档简介
(共25张PPT)
Reading task
FINDING THE SOLUTION
Unit1 Workbook
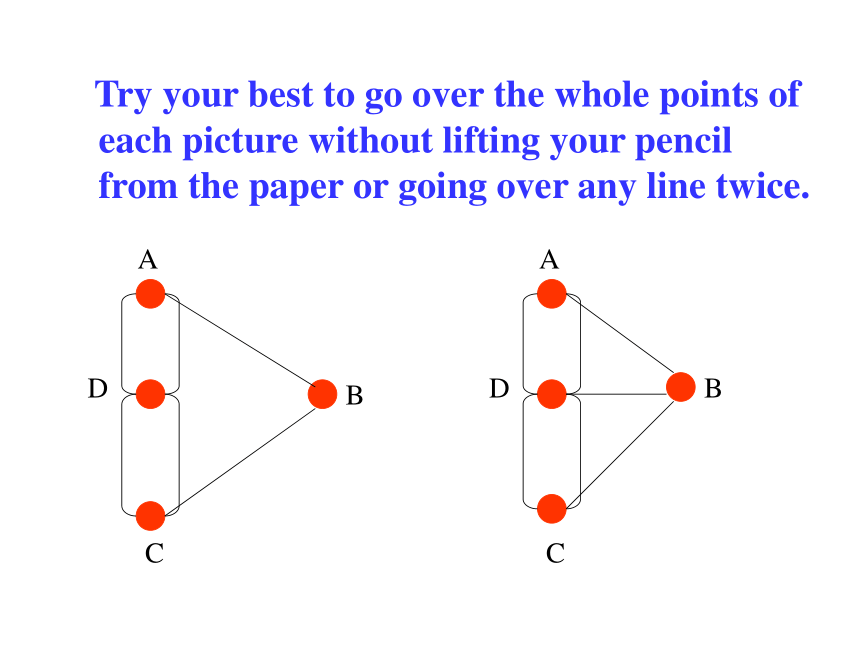
Try your best to go over the whole points of each picture without lifting your pencil from the paper or going over any line twice.
A
A
D
D
B
B
C
C
Topology--Euler path
Euler
What’s Euler’s puzzle
Konigsberg is an island and there is a river breaking here into two parts.
“Seven Bridges of Konigsberg” and the famous “Euler path”.
People wondered if they could walk around the city by crossing the seven bridges without going over any of them twice or going back on himself, but Euler found he couldn’t cross all the seven ones. This is Euler’s puzzle.
The first stage in his research is to find the problem that he could cross six of the bridges without going over any of them twice or going back on himself, but he couldn’t cross all seven.
How did Euler prepare for his research
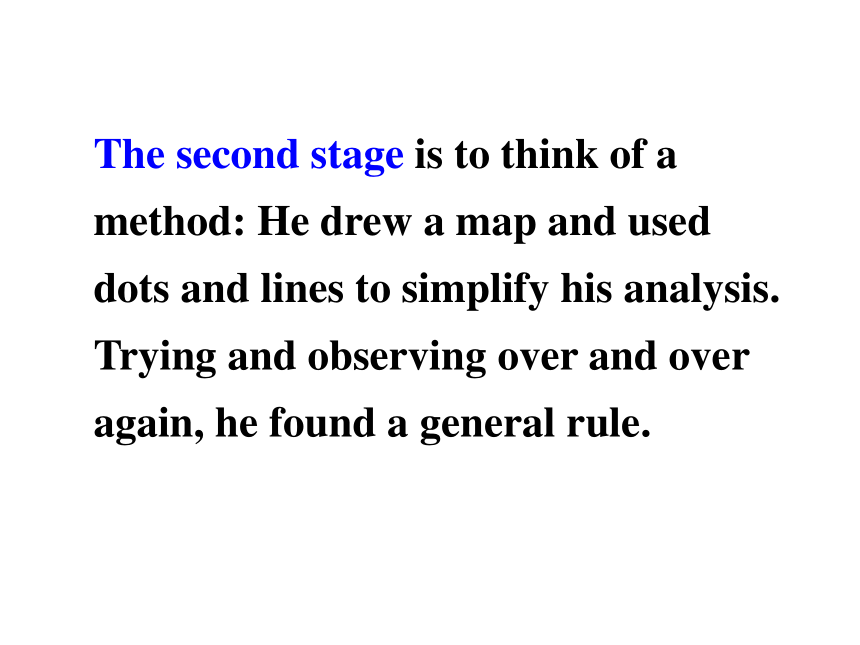
The second stage is to think of a
method: He drew a map and used
dots and lines to simplify his analysis.
Trying and observing over and over
again, he found a general rule.
It is topology. Euler’s theory is called “The Euler path”, which is expressed like this: If a figure has more than two odd points, you can’t go over it without lifting your pencil from the page or going over a line twice. So the general rule that Euler found is the even points and the odd points .
What are the theories
Conclusion
Euler’s theory (一笔画)
可以一笔画只有两种情况:
1. 没有奇数顶点。
2. 只有两个奇数顶点。
同学们如果对此类问题感兴趣, 可登录:
http://www.e-/bbs/index.php
Read the text and find out the answers to the following questions.
How did Euler find a problem
What’s the general rule to the puzzle
What branch of mathematics did Euler start
When he walked around the town and over the bridges of Konigsberg, he was surprised to find that he could cross six of the bridges without going over any of them twice or going back on himself, but he couldn’t cross all seven.
How did Euler find a problem
What’s the general rule to the puzzle
What branch of mathematics did Euler start
If a figure has more than two odd points, you can’t go over it without lifting your pencil from the page or going over a line twice.
He started a whole new branch of mathematics called “topology”.
Fill in the chart after reading the text.
How many bridges could Euler cross without going across any of them twice Six
How did he try to solve the puzzle
What is an “odd”
point
By turning the map into a diagram.
One which has an odd number of lines going to it.
How many odd points are there in Fig 2 on page 45
How many odd points are there in Fig 4 on page 45
Four
Two
What is Euler’s rule
Did his rule work with Figs 2 and 4
If a figure has more than two odd points, you cannot go over it without lifting your pencil from the page or without going over a line twice.
Yes
Look at the following pictures.
Check to see if you are right by using a pencil to go over the diagram. Remember not to miss any points or go over any line twice. Give a reason if there is no path.
In pairs discuss the life and work of any scientist that you know. Explain their achievements and recount stories that show interesting aspects of their character and their work. Talk about how they achieved their success.
Speaking task
Was it because of his / her talent, intelligence, hard work, persistence, confidence, curiosity, enthusiasm or luck Prepare to give a talk on your chosen scientist to the class.
The following questions may help you with your discussion.
1.Who is the scientist you admire most
2. What nationality is this scientist
3.What kind of family did he/she come from
4.What kind of education did he/she receive
5.What did he/she achieve in his/her
scientific work
6. Why did he/she achieve great success
Now write a report about your scientist, his/ her life, achievements and the key to his / her success. Before you begin to write, remember to put your information under three headings:
Life
Achievements
Key to success.
Writing
Please plan your report according to these steps:
Introduction to the scientist, including dates, where he / she lived and worked and which branch of science;
Life of the scientist;
Achievements of your chosen scientist;
Key to his / her success;
General summary of his/her importance in science and why you chose him/her.
Reading task
FINDING THE SOLUTION
Unit1 Workbook
Try your best to go over the whole points of each picture without lifting your pencil from the paper or going over any line twice.
A
A
D
D
B
B
C
C
Topology--Euler path
Euler
What’s Euler’s puzzle
Konigsberg is an island and there is a river breaking here into two parts.
“Seven Bridges of Konigsberg” and the famous “Euler path”.
People wondered if they could walk around the city by crossing the seven bridges without going over any of them twice or going back on himself, but Euler found he couldn’t cross all the seven ones. This is Euler’s puzzle.
The first stage in his research is to find the problem that he could cross six of the bridges without going over any of them twice or going back on himself, but he couldn’t cross all seven.
How did Euler prepare for his research
The second stage is to think of a
method: He drew a map and used
dots and lines to simplify his analysis.
Trying and observing over and over
again, he found a general rule.
It is topology. Euler’s theory is called “The Euler path”, which is expressed like this: If a figure has more than two odd points, you can’t go over it without lifting your pencil from the page or going over a line twice. So the general rule that Euler found is the even points and the odd points .
What are the theories
Conclusion
Euler’s theory (一笔画)
可以一笔画只有两种情况:
1. 没有奇数顶点。
2. 只有两个奇数顶点。
同学们如果对此类问题感兴趣, 可登录:
http://www.e-/bbs/index.php
Read the text and find out the answers to the following questions.
How did Euler find a problem
What’s the general rule to the puzzle
What branch of mathematics did Euler start
When he walked around the town and over the bridges of Konigsberg, he was surprised to find that he could cross six of the bridges without going over any of them twice or going back on himself, but he couldn’t cross all seven.
How did Euler find a problem
What’s the general rule to the puzzle
What branch of mathematics did Euler start
If a figure has more than two odd points, you can’t go over it without lifting your pencil from the page or going over a line twice.
He started a whole new branch of mathematics called “topology”.
Fill in the chart after reading the text.
How many bridges could Euler cross without going across any of them twice Six
How did he try to solve the puzzle
What is an “odd”
point
By turning the map into a diagram.
One which has an odd number of lines going to it.
How many odd points are there in Fig 2 on page 45
How many odd points are there in Fig 4 on page 45
Four
Two
What is Euler’s rule
Did his rule work with Figs 2 and 4
If a figure has more than two odd points, you cannot go over it without lifting your pencil from the page or without going over a line twice.
Yes
Look at the following pictures.
Check to see if you are right by using a pencil to go over the diagram. Remember not to miss any points or go over any line twice. Give a reason if there is no path.
In pairs discuss the life and work of any scientist that you know. Explain their achievements and recount stories that show interesting aspects of their character and their work. Talk about how they achieved their success.
Speaking task
Was it because of his / her talent, intelligence, hard work, persistence, confidence, curiosity, enthusiasm or luck Prepare to give a talk on your chosen scientist to the class.
The following questions may help you with your discussion.
1.Who is the scientist you admire most
2. What nationality is this scientist
3.What kind of family did he/she come from
4.What kind of education did he/she receive
5.What did he/she achieve in his/her
scientific work
6. Why did he/she achieve great success
Now write a report about your scientist, his/ her life, achievements and the key to his / her success. Before you begin to write, remember to put your information under three headings:
Life
Achievements
Key to success.
Writing
Please plan your report according to these steps:
Introduction to the scientist, including dates, where he / she lived and worked and which branch of science;
Life of the scientist;
Achievements of your chosen scientist;
Key to his / her success;
General summary of his/her importance in science and why you chose him/her.