北师大版七年级下册数学第一章课时作业:6 第2课时 完全平方公式的应用(Word版 含答案)
文档属性
| 名称 | 北师大版七年级下册数学第一章课时作业:6 第2课时 完全平方公式的应用(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 55.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 00:00:00 | ||
图片预览



文档简介
6.2完全平方公式的应用
知识点
1 利用完全平方公式进行简便运算
1.计算:992=( - )2= 2- × × + 2=9801.?
2.将9.52变形正确的是
( )
A.9.52=92+0.52
B.9.52=(10+0.5)(10-0.5)
C.9.52=102-2×10×0.5+0.52
D.9.52=92+9×0.5+0.52
3.利用完全平方公式进行简便计算:
(1)3012; (2).
知识点
2 与完全平方公式有关的综合运算
4.(a-b+c)(-a+b-c)与下列哪个式子相等
( )
A.-(a-b+c)2
B.c2-(a-b)2
C.(a-b)2-c2
D.c-a+b2
5.化简:(a+1)2-(a-1)2= .?
6.计算:(1)(a+2)2-a2;
(2)(y+x+6)(y-x+6);
(3)(2x-y-3)2.
7.如图,在边长为2a(a>2)的正方形中央剪去一个边长为a+2的小正方形,将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积是多少?
8.若xy=12,(x-3y)2=25,则(x+3y)2的值为
( )
A.196
B.169
C.156
D.144
9.若等式(x-5)2-b=x2+ax+19成立,则a+b的值为
( )
A.16
B.-16
C.4
D.-4
10.计算:20212-4042×2020+20202.
11.计算:(1)(2x+3y)2-(2x-3y)2;
(2)(a+3b)2-2(a+3b)(a-3b)+(a-3b)2.
12.有这样一道题:“先化简,再求值:[(a+2)2-(a+1)2](2a-3)-4a2,其中a=-2021.”小号同学在解题时把“a=-2021”错抄成了“a=2021”,但他的计算结果也是正确的,你能解释一下这是怎么回事吗?
13.已知(a+b)2=5,(a-b)2=3,求下列式子的值:
(1)a2+b2; (2)6ab.
14.已知x2-2x+y2+6y+10=0,求x+y的值.
15.
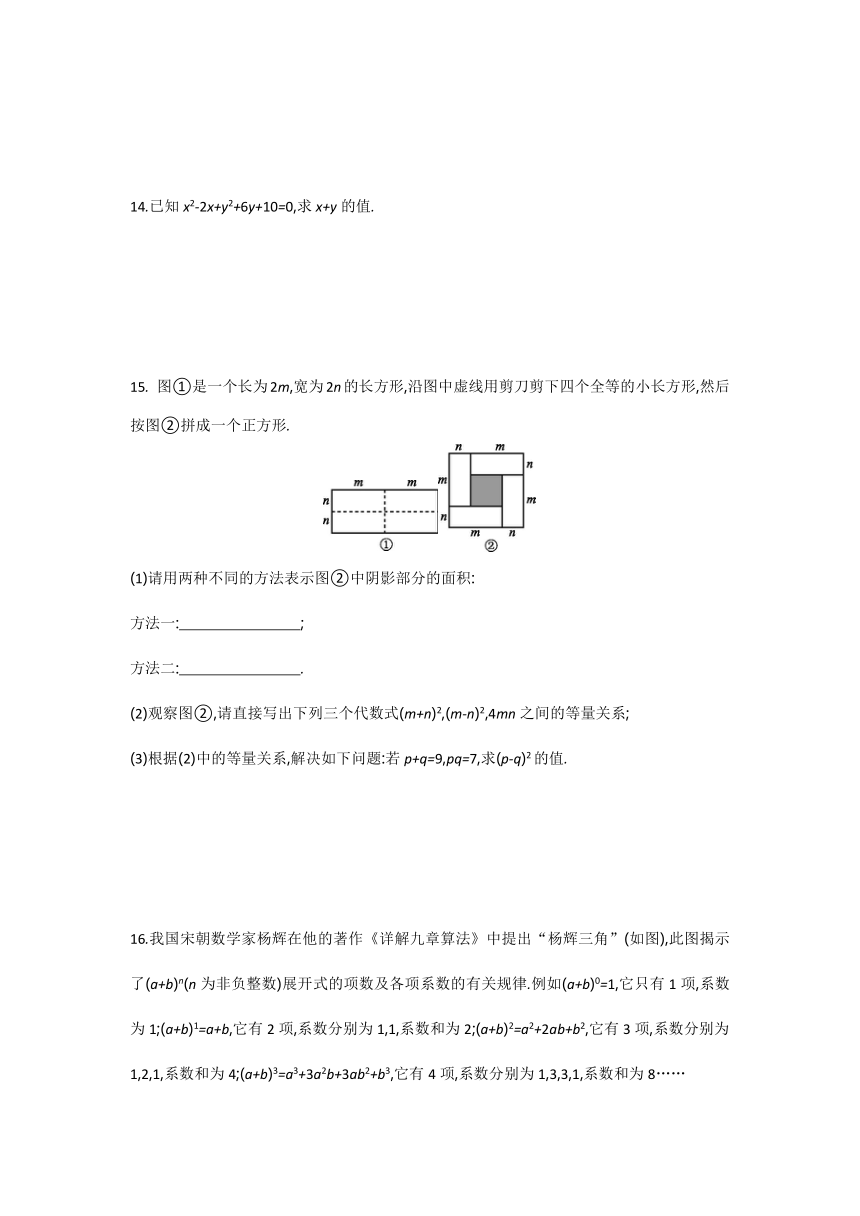
图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下四个全等的小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积:
方法一: ;?
方法二: .?
(2)观察图②,请直接写出下列三个代数式(m+n)2,(m-n)2,4mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p-q)2的值.
16.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如(a+b)0=1,它只有1项,系数为1;(a+b)1=a+b,它有2项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有3项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有4项,系数分别为1,3,3,1,系数和为8……
根据以上规律,解答下列问题:
(1)(a+b)4的展开式共有 项,系数分别为 ;?
(2)(a+b)n的展开式共有 项,系数和为 ;?
(3)计算:25+5×24+10×23+10×22+5×2+1.
参考答案
1.100 1 100 2 100 1 1
2.C
3.解:(1)3012=(300+1)2=3002+2×300×1+12=90601.
(2)==302+2×30×+=900+30+=930.
4.A
5.4a
6.解:(1)原式=a2+4a+4-a2
=4a+4.
(2)原式=[(y+6)+x][(y+6)-x]
=(y+6)2-x2
=y2+12y+36-x2.
(3)原式=[(2x-y)-3]2
=(2x-y)2-2×(2x-y)×3+32
=4x2-4xy+y2-6(2x-y)+9
=4x2-4xy+y2-12x+6y+9.
7.解:由题意可知,平行四边形的面积等于左图中大正方形的面积减去小正方形的面积,即(2a)2-(a+2)2=4a2-a2-4a-4=3a2-4a-4.
8.B 解析:
(x+3y)2=(x-3y)2+12xy=25+12×12=169.
9.D 解析:
等式整理,得x2-10x+25-b=x2+ax+19,所以a=-10,b=6,则a+b=-10+6=-4.
10.解:20212-4042×2020+20202
=20212-2×2021×2020+20202
=(2021-2020)2
=12
=1.
11.解:(1)(2x+3y)2-(2x-3y)2
=4x2+12xy+9y2-(4x2-12xy+9y2)
=24xy.
(2)原式=[(a+3b)-(a-3b)]2
=36b2.
12.解:原式=[(a2+4a+4)-(a2+2a+1)](2a-3)-4a2=(2a+3)(2a-3)-4a2=4a2-9-4a2=-9.
因为结果中不含字母a,所以小号同学在解题时把“a=-2021”错抄成了“a=2021”,但他的计算结果也是正确的.
13.解:(1)因为(a+b)2=5,(a-b)2=3,
所以a2+2ab+b2=5,a2-2ab+b2=3,
所以2(a2+b2)=8,
所以a2+b2=4.
(2)因为a2+b2=4,
所以4+2ab=5,
所以ab=,
所以6ab=3.
14.解:原等式变形为(x2-2x+1)+(y2+6y+9)=0,即(x-1)2+(y+3)2=0,当且仅当x-1=0且y+3=0时,等式成立,
所以x=1,y=-3,
所以x+y=1-3=-2.
15.解:(1)(m-n)2 (m+n)2-4mn
(2)(m-n)2=(m+n)2-4mn.
(3)当p+q=9,pq=7时,
(p-q)2=(p+q)2-4pq=92-4×7=81-28=53.
16.解:(1)根据题意,知(a+b)4的展开式共有5项,各项系数分别为1,1+3,3+3,3+1,1,即1,4,6,4,1.
(2)(a+b)n的展开式共有(n+1)项,当a=b=1时,(a+b)n=2n,即系数和为2n.
(3)原式=25+5×24×1+10×23×12+10×22×13+5×2×14+15=(2+1)5=243.
知识点
1 利用完全平方公式进行简便运算
1.计算:992=( - )2= 2- × × + 2=9801.?
2.将9.52变形正确的是
( )
A.9.52=92+0.52
B.9.52=(10+0.5)(10-0.5)
C.9.52=102-2×10×0.5+0.52
D.9.52=92+9×0.5+0.52
3.利用完全平方公式进行简便计算:
(1)3012; (2).
知识点
2 与完全平方公式有关的综合运算
4.(a-b+c)(-a+b-c)与下列哪个式子相等
( )
A.-(a-b+c)2
B.c2-(a-b)2
C.(a-b)2-c2
D.c-a+b2
5.化简:(a+1)2-(a-1)2= .?
6.计算:(1)(a+2)2-a2;
(2)(y+x+6)(y-x+6);
(3)(2x-y-3)2.
7.如图,在边长为2a(a>2)的正方形中央剪去一个边长为a+2的小正方形,将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积是多少?
8.若xy=12,(x-3y)2=25,则(x+3y)2的值为
( )
A.196
B.169
C.156
D.144
9.若等式(x-5)2-b=x2+ax+19成立,则a+b的值为
( )
A.16
B.-16
C.4
D.-4
10.计算:20212-4042×2020+20202.
11.计算:(1)(2x+3y)2-(2x-3y)2;
(2)(a+3b)2-2(a+3b)(a-3b)+(a-3b)2.
12.有这样一道题:“先化简,再求值:[(a+2)2-(a+1)2](2a-3)-4a2,其中a=-2021.”小号同学在解题时把“a=-2021”错抄成了“a=2021”,但他的计算结果也是正确的,你能解释一下这是怎么回事吗?
13.已知(a+b)2=5,(a-b)2=3,求下列式子的值:
(1)a2+b2; (2)6ab.
14.已知x2-2x+y2+6y+10=0,求x+y的值.
15.
图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下四个全等的小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积:
方法一: ;?
方法二: .?
(2)观察图②,请直接写出下列三个代数式(m+n)2,(m-n)2,4mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p-q)2的值.
16.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如(a+b)0=1,它只有1项,系数为1;(a+b)1=a+b,它有2项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有3项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有4项,系数分别为1,3,3,1,系数和为8……
根据以上规律,解答下列问题:
(1)(a+b)4的展开式共有 项,系数分别为 ;?
(2)(a+b)n的展开式共有 项,系数和为 ;?
(3)计算:25+5×24+10×23+10×22+5×2+1.
参考答案
1.100 1 100 2 100 1 1
2.C
3.解:(1)3012=(300+1)2=3002+2×300×1+12=90601.
(2)==302+2×30×+=900+30+=930.
4.A
5.4a
6.解:(1)原式=a2+4a+4-a2
=4a+4.
(2)原式=[(y+6)+x][(y+6)-x]
=(y+6)2-x2
=y2+12y+36-x2.
(3)原式=[(2x-y)-3]2
=(2x-y)2-2×(2x-y)×3+32
=4x2-4xy+y2-6(2x-y)+9
=4x2-4xy+y2-12x+6y+9.
7.解:由题意可知,平行四边形的面积等于左图中大正方形的面积减去小正方形的面积,即(2a)2-(a+2)2=4a2-a2-4a-4=3a2-4a-4.
8.B 解析:
(x+3y)2=(x-3y)2+12xy=25+12×12=169.
9.D 解析:
等式整理,得x2-10x+25-b=x2+ax+19,所以a=-10,b=6,则a+b=-10+6=-4.
10.解:20212-4042×2020+20202
=20212-2×2021×2020+20202
=(2021-2020)2
=12
=1.
11.解:(1)(2x+3y)2-(2x-3y)2
=4x2+12xy+9y2-(4x2-12xy+9y2)
=24xy.
(2)原式=[(a+3b)-(a-3b)]2
=36b2.
12.解:原式=[(a2+4a+4)-(a2+2a+1)](2a-3)-4a2=(2a+3)(2a-3)-4a2=4a2-9-4a2=-9.
因为结果中不含字母a,所以小号同学在解题时把“a=-2021”错抄成了“a=2021”,但他的计算结果也是正确的.
13.解:(1)因为(a+b)2=5,(a-b)2=3,
所以a2+2ab+b2=5,a2-2ab+b2=3,
所以2(a2+b2)=8,
所以a2+b2=4.
(2)因为a2+b2=4,
所以4+2ab=5,
所以ab=,
所以6ab=3.
14.解:原等式变形为(x2-2x+1)+(y2+6y+9)=0,即(x-1)2+(y+3)2=0,当且仅当x-1=0且y+3=0时,等式成立,
所以x=1,y=-3,
所以x+y=1-3=-2.
15.解:(1)(m-n)2 (m+n)2-4mn
(2)(m-n)2=(m+n)2-4mn.
(3)当p+q=9,pq=7时,
(p-q)2=(p+q)2-4pq=92-4×7=81-28=53.
16.解:(1)根据题意,知(a+b)4的展开式共有5项,各项系数分别为1,1+3,3+3,3+1,1,即1,4,6,4,1.
(2)(a+b)n的展开式共有(n+1)项,当a=b=1时,(a+b)n=2n,即系数和为2n.
(3)原式=25+5×24×1+10×23×12+10×22×13+5×2×14+15=(2+1)5=243.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
