沪科版 七年级下册数学 第10章 相交线 平行线与平移单元测试(word版含答案)
文档属性
| 名称 | 沪科版 七年级下册数学 第10章 相交线 平行线与平移单元测试(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 305.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 17:51:29 | ||
图片预览


文档简介
七年级下册数学沪科版第10章
相交线
平行线与平移
时间:60分钟
满分:100分
一、选择题(每题3分,共30分)
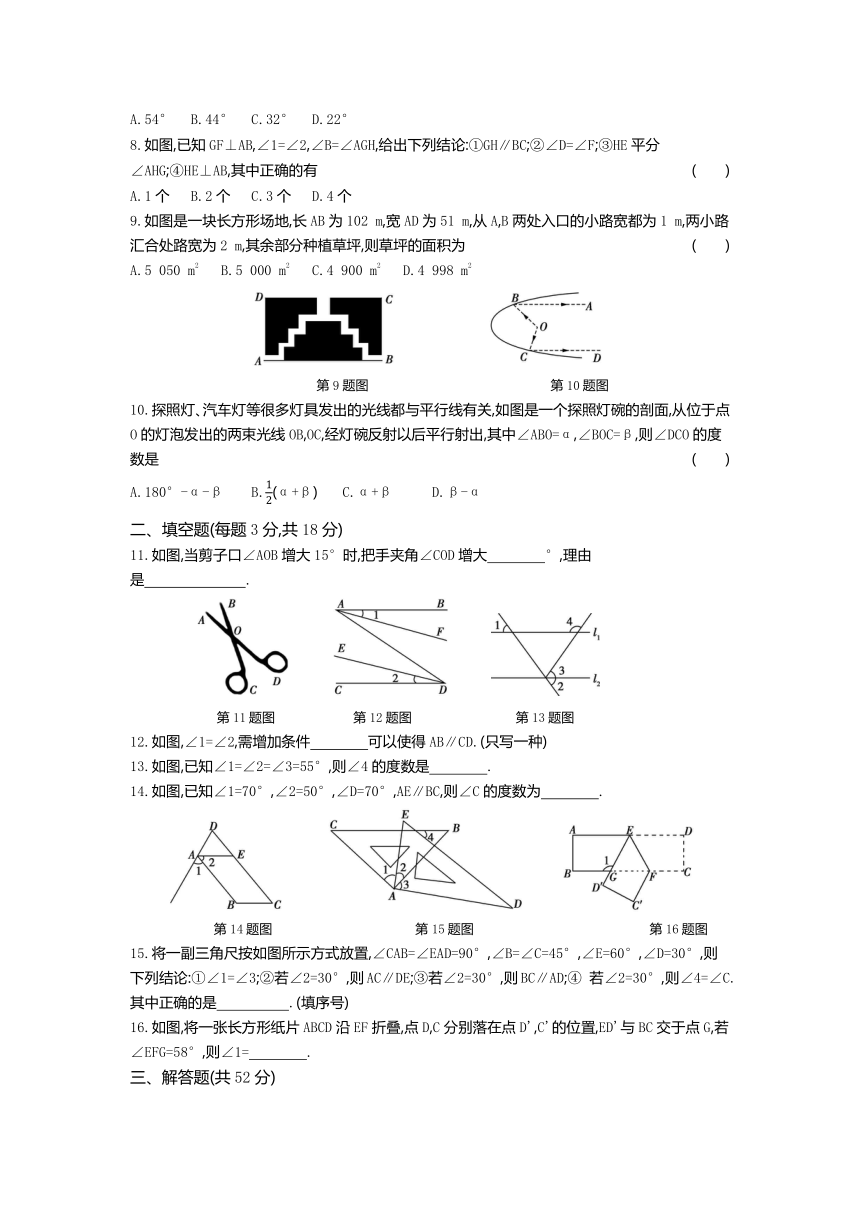
1.下列四个图案中,运用了图形的平移进行图案设计的是
( )
A B
C D
2.如图,在江边有一赵庄,现要建一码头,为了使赵庄人乘船最方便,码头应建在( )
A.A点
B.B点
C.C点
D.D点
第2题图 第3题图
第4题图
3.如图,对顶角的对数为
( )
A.4
B.5
C.6
D.8
4.如图,下列说法正确的是
( )
A.∠A与∠ABC是同旁内角
B.∠3与∠1是同旁内角
C.∠2与∠3是内错角
D.∠1与∠2是同位角
5.如图,下列条件不能判定直线l1∥l2的是
( )
A.∠1=∠3
B.∠1=∠4
C.∠2+∠3=180°
D.∠3=∠5
第5题图 第6题图 第7题图 第8题图
6.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=
( )
A.158°
B.136°
C.134°
D.120°
7.如图,已知DC∥FP,∠1=∠2,∠FED=32°,∠AGF=76°,FH平分∠EFG,则∠PFH的度数是
( )
A.54°
B.44°
C.32°
D.22°
8.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,给出下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
9.如图是一块长方形场地,长AB为102
m,宽AD为51
m,从A,B两处入口的小路宽都为1
m,两小路汇合处路宽为2
m,其余部分种植草坪,则草坪的面积为
( )
A.5
050
m2
B.5
000
m2
C.4
900
m2
D.4
998
m2
第9题图 第10题图
10.探照灯、汽车灯等很多灯具发出的光线都与平行线有关,如图是一个探照灯碗的剖面,从位于点O的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是
( )
A.180°-α-β
B.(α+β)
C.α+β
D.β-α
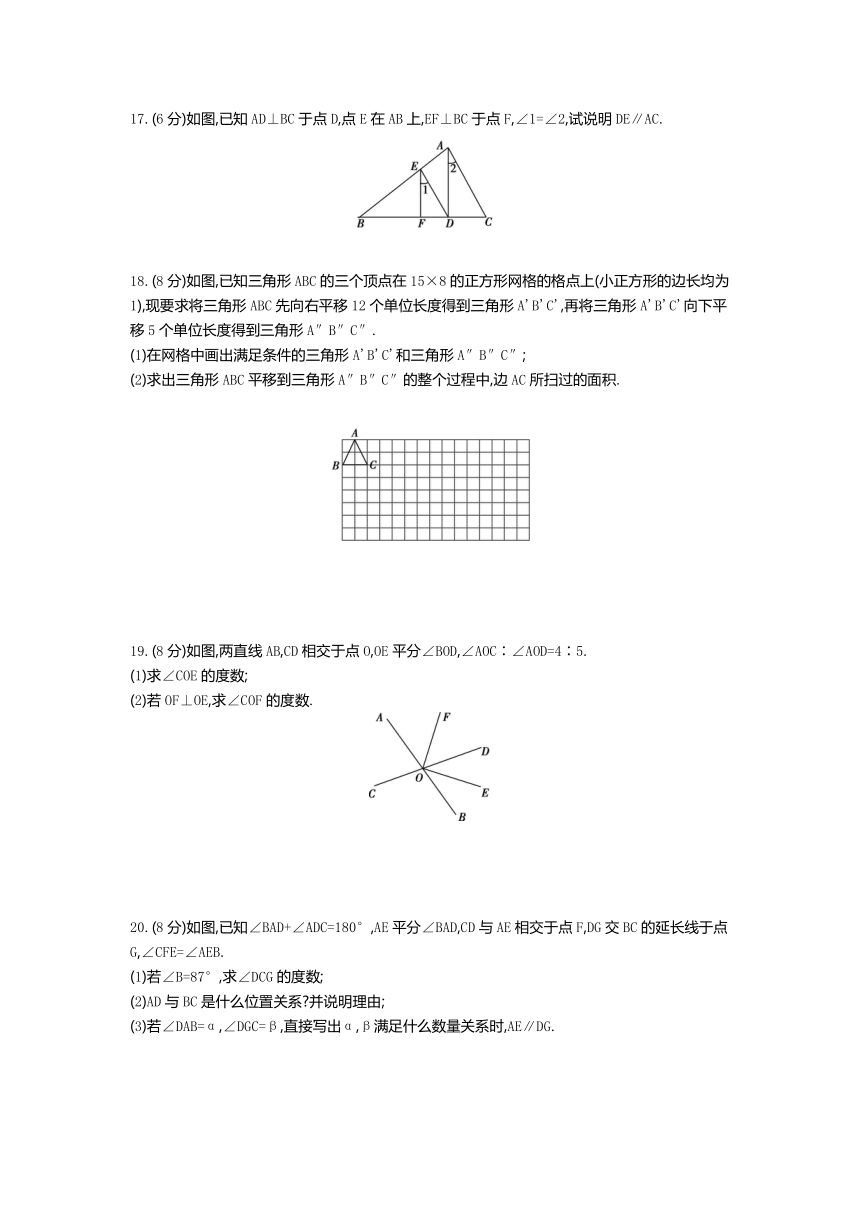
二、填空题(每题3分,共18分)
11.如图,当剪子口∠AOB增大15°时,把手夹角∠COD增大 °,理由是 .
?
第11题图 第12题图 第13题图
12.如图,∠1=∠2,需增加条件 可以使得AB∥CD.(只写一种)?
13.如图,已知∠1=∠2=∠3=55°,则∠4的度数是 .?
14.如图,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC,则∠C的度数为 .?
第14题图 第15题图
第16题图
15.将一副三角尺按如图所示方式放置,∠CAB=∠EAD=90°,∠B=∠C=45°,∠E=60°,∠D=30°,则下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④
若∠2=30°,则∠4=∠C.其中正确的是 .(填序号)?
16.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D',C'的位置,ED'与BC交于点G,若∠EFG=58°,则∠1= .?
三、解答题(共52分)
17.(6分)如图,已知AD⊥BC于点D,点E在AB上,EF⊥BC于点F,∠1=∠2,试说明DE∥AC.
18.(8分)如图,已知三角形ABC的三个顶点在15×8的正方形网格的格点上(小正方形的边长均为1),现要求将三角形ABC先向右平移12个单位长度得到三角形A'B'C',再将三角形A'B'C'向下平移5个单位长度得到三角形A″B″C″.
(1)在网格中画出满足条件的三角形A'B'C'和三角形A″B″C″;
(2)求出三角形ABC平移到三角形A″B″C″的整个过程中,边AC所扫过的面积.
19.(8分)如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=4∶5.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
20.(8分)如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于点F,DG交BC的延长线于点G,∠CFE=∠AEB.
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α,β满足什么数量关系时,AE∥DG.
21.(10分)如图,已知CD∥EF,CH∥AB,∠EFG+∠BCD=∠ABC.试说明AB∥GF.
22.(12分)已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=50°,∠DCP=30°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,AK、CK分别平分∠BAP、∠DCP,请写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD下方,AK、CK分别平分∠BAP、∠DCP,请写出∠AKC与∠APC之间的数量关系,并说明理由.
第10章 综合能力检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
A
A
C
D
B
B
D
11.15 对顶角相等 12.∠FAD=∠EDA(答案不唯一)
13.125° 14.50° 15.①②④ 16.116°
1.A
2.A 【解析】
在连接直线外一点与直线上各点的线段中,垂线段最短,所以码头应建在A点.故选A.
3.D 【解析】 由对顶角的定义,可知点A,B,C,N处各有2对对顶角,所以共有8对对顶角.故选D.
4.A 【解析】 根据同位角、内错角、同旁内角的定义,可知∠A与∠ABC是同旁内角,∠3与∠1是内错角,∠2与∠3是同位角,∠1与∠2既不是同位角、内错角,也不是同旁内角.故选A.
5.A 【解析】 B项,根据内错角相等,两直线平行,可判定l1∥l2;C项,根据同旁内角互补,两直线平行,可判定l1∥l2;D项,根据同位角相等,两直线平行,可判定l1∥l2.故选A.
6.C 【解析】 如图,过点E作EF∥AB,因为AB∥CD,所以AB∥CD∥EF,所以∠C=∠FEC,∠BAE=∠FEA.因为∠C=44°,∠AEC为直角,所以∠FEC=44°,∠BAE=∠AEF=90°-44°=46°,所以∠1=180°-∠BAE=180°-46°=134°.故选C.
7.D 【解析】 如图,因为DC∥FP,所以∠EFP=∠FED=32°.因为∠1=∠2,所以FP∥AB,所以∠GFP=∠AGF=76°,所以∠GFE=∠GFP+∠EFP=76°+32°=108°,又因为FH平分∠GFE,所以∠GFH=∠GFE=54°,所以∠PFH=∠GFP-∠GFH=76°-54°=22°.故选D.
8.B 【解析】 因为∠B=∠AGH,所以GH∥BC,所以∠1=∠HGM,因为∠1=∠2,所以∠2=∠HGM,所以DE∥GF,因为
GF⊥AB,所以HE⊥AB,故①④正确;因为GF∥DE,所以∠D=∠1,因为∠1=∠CMF,根据已知条件不能推出∠F=∠CMF,即不能推出∠D=∠F,故②错误;因为∠AHG=∠2+∠AHE,根据已知条件不能推出∠2=∠AHE,故③错误.综上,正确的有2个,故选B.
9.B 【解析】 由题图可知,长方形场地ABCD中去掉路后,草坪正好可以拼成一个新的长方形,且它的长为102-2=100(m),宽为51-1=50(m).所以草坪的面积为100×50=5
000(m2).故选B.
10.D 【解析】 如图,过点O作直线EF∥AB,则EF∥CD.因为AB∥EF,所以∠1=∠ABO=α.因为EF∥CD,所以∠DCO=∠2=β-α.故选D.
11.15 对顶角相等
12.∠FAD=∠EDA(答案不唯一) 【解析】 因为∠BAD=∠1+∠FAD,∠ADC=∠2+∠EDA,且∠BAD与∠ADC是内错角,如果∠BAD=∠ADC,那么AB∥CD,那么∠1+∠FAD=∠2+∠EDA,又因为∠1=∠2,所以∠FAD=∠EDA.
13.125° 【解析】 给各角标上序号,如图所示.因为∠1=∠2,∠2=∠5,所以∠1=∠5,所以l1∥l2,所以∠3+∠6=180°.因为∠3=55°,所以∠6=180°-55°=125°,所以∠4=∠6=125°.
14.50° 【解析】 因为∠1=70°,∠D=70°,所以∠1=∠D,所以AB∥CD,所以∠2+∠AEC=180°.又因为AE∥BC,所以∠C+∠AEC=180°,所以∠C=∠2=50°.
15.①②④ 【解析】
因为∠CAB=∠EAD=90°,∠1=∠CAB-∠2,∠3=∠EAD-∠2,所以∠1=∠3,故①正确;因为∠2=30°,所以∠1=90°-30°=60°,因为∠E=60°,所以∠1=∠E,所以AC∥DE,故②正确;因为∠2=30°,所以∠3=90°-30°=60°,因为∠B=45°,所以∠B≠∠3,所以BC与AD不平行,故③错误;由②得AC∥DE,所以∠4=∠C,故④正确.综上,正确的是①②④.
16.116° 【解析】 因为四边形ABCD为长方形,所以AD∥BC,所以∠1=∠DEG,∠DEF=∠EFG=58°.由折叠的性质,可得∠DEF=∠GEF=58°,所以∠1=∠DEG=∠GEF+∠DEF=116°.
17.【解析】 如图,因为AD⊥BC于点D,EF⊥BC于点F,
所以AD∥EF,所以∠1=∠3.
因为∠1=∠2,所以∠2=∠3,
所以DE∥AC.
18.【解析】 (1)三角形A'B'C'和三角形A″B″C″如图所示.
(2)由(1)中图形,知边AC所扫过的面积为12×2+5×1-×2×1=28.
19.【解析】
(1)因为∠AOC∶∠AOD=4∶5,
所以可设∠AOC=4x,∠AOD=5x,
则4x+5x=180°,解得x=20°,
所以∠AOC=80°,∠AOD=100°.
又因为OE平分∠BOD,∠BOD=∠AOC=80°,
所以∠EOD=∠BOE=40°,
所以∠COE=180°-40°=140°.
(2)因为OF⊥OE,所以∠FOE=90°,
所以∠FOD=50°,
所以∠COF=180°-50°=130°.
20.【解析】 (1)因为∠BAD+∠ADC=180°,
所以AB∥CD,所以∠DCG=∠B=87°.
(2)AD∥BC.理由如下:
因为AB∥CD,所以∠BAF=∠CFE,
又因为AE平分∠BAD,所以∠BAF=∠FAD,
所以∠DAF=∠CFE,
因为∠CFE=∠AEB,所以∠DAF=∠AEB,所以AD∥BC.
(3)当α=2β时,AE∥DG.理由如下:
若AE∥DG,则∠DGC=∠AEB=∠DAE=∠DAB,
即当α=2β时,AE∥DG.
21.【解析】 如图,延长CD交直线GF于点M.
因为CD∥EF,
所以∠M=∠EFG.
因为CH∥AB,所以∠HCB+∠ABC=180°,
因为∠EFG+∠BCD=∠ABC,
所以∠EFG+∠BCD+∠HCB=180°,
所以∠M+∠BCD+∠HCB=180°,
所以CH∥GF,所以AB∥GF.
22.【解析】 (1)如图1,过P作PE∥AB,
因为AB∥CD,
所以PE∥AB∥CD,
所以∠APE=∠BAP,∠CPE=∠DCP,
所以∠APC=∠APE+∠CPE=∠BAP+∠DCP=50°+30°=80°.
(2)∠AKC=∠APC.理由如下:
如图2,过K作KE∥AB,过P作PF∥AB.
因为AB∥CD,所以KE∥AB∥CD,
所以∠AKE=∠BAK,∠CKE=∠DCK,
所以∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
同理可得,∠APC=∠BAP+∠DCP,
因为∠BAP与∠DCP的角平分线相交于点K,
所以∠BAK+∠DCK=∠BAP+∠DCP=(∠BAP+∠DCP)=∠APC,
所以∠AKC=∠APC.
(3)∠AKC=∠APC.理由如下:
如图3,过K作KE∥AB,过P作PF∥AB.
因为AB∥CD,所以KE∥AB∥CD,
所以∠BAK=∠AKE,∠DCK=∠CKE,
所以∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,
同理可得,∠APC=∠BAP-∠DCP,
因为∠BAP与∠DCP的角平分线相交于点K,
所以∠BAK-∠DCK=∠BAP-∠DCP=(∠BAP-∠DCP)=∠APC,
所以∠AKC=∠APC.
相交线
平行线与平移
时间:60分钟
满分:100分
一、选择题(每题3分,共30分)
1.下列四个图案中,运用了图形的平移进行图案设计的是
( )
A B
C D
2.如图,在江边有一赵庄,现要建一码头,为了使赵庄人乘船最方便,码头应建在( )
A.A点
B.B点
C.C点
D.D点
第2题图 第3题图
第4题图
3.如图,对顶角的对数为
( )
A.4
B.5
C.6
D.8
4.如图,下列说法正确的是
( )
A.∠A与∠ABC是同旁内角
B.∠3与∠1是同旁内角
C.∠2与∠3是内错角
D.∠1与∠2是同位角
5.如图,下列条件不能判定直线l1∥l2的是
( )
A.∠1=∠3
B.∠1=∠4
C.∠2+∠3=180°
D.∠3=∠5
第5题图 第6题图 第7题图 第8题图
6.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=
( )
A.158°
B.136°
C.134°
D.120°
7.如图,已知DC∥FP,∠1=∠2,∠FED=32°,∠AGF=76°,FH平分∠EFG,则∠PFH的度数是
( )
A.54°
B.44°
C.32°
D.22°
8.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,给出下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
9.如图是一块长方形场地,长AB为102
m,宽AD为51
m,从A,B两处入口的小路宽都为1
m,两小路汇合处路宽为2
m,其余部分种植草坪,则草坪的面积为
( )
A.5
050
m2
B.5
000
m2
C.4
900
m2
D.4
998
m2
第9题图 第10题图
10.探照灯、汽车灯等很多灯具发出的光线都与平行线有关,如图是一个探照灯碗的剖面,从位于点O的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是
( )
A.180°-α-β
B.(α+β)
C.α+β
D.β-α
二、填空题(每题3分,共18分)
11.如图,当剪子口∠AOB增大15°时,把手夹角∠COD增大 °,理由是 .
?
第11题图 第12题图 第13题图
12.如图,∠1=∠2,需增加条件 可以使得AB∥CD.(只写一种)?
13.如图,已知∠1=∠2=∠3=55°,则∠4的度数是 .?
14.如图,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC,则∠C的度数为 .?
第14题图 第15题图
第16题图
15.将一副三角尺按如图所示方式放置,∠CAB=∠EAD=90°,∠B=∠C=45°,∠E=60°,∠D=30°,则下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④
若∠2=30°,则∠4=∠C.其中正确的是 .(填序号)?
16.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D',C'的位置,ED'与BC交于点G,若∠EFG=58°,则∠1= .?
三、解答题(共52分)
17.(6分)如图,已知AD⊥BC于点D,点E在AB上,EF⊥BC于点F,∠1=∠2,试说明DE∥AC.
18.(8分)如图,已知三角形ABC的三个顶点在15×8的正方形网格的格点上(小正方形的边长均为1),现要求将三角形ABC先向右平移12个单位长度得到三角形A'B'C',再将三角形A'B'C'向下平移5个单位长度得到三角形A″B″C″.
(1)在网格中画出满足条件的三角形A'B'C'和三角形A″B″C″;
(2)求出三角形ABC平移到三角形A″B″C″的整个过程中,边AC所扫过的面积.
19.(8分)如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=4∶5.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
20.(8分)如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于点F,DG交BC的延长线于点G,∠CFE=∠AEB.
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α,β满足什么数量关系时,AE∥DG.
21.(10分)如图,已知CD∥EF,CH∥AB,∠EFG+∠BCD=∠ABC.试说明AB∥GF.
22.(12分)已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=50°,∠DCP=30°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,AK、CK分别平分∠BAP、∠DCP,请写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD下方,AK、CK分别平分∠BAP、∠DCP,请写出∠AKC与∠APC之间的数量关系,并说明理由.
第10章 综合能力检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
A
A
C
D
B
B
D
11.15 对顶角相等 12.∠FAD=∠EDA(答案不唯一)
13.125° 14.50° 15.①②④ 16.116°
1.A
2.A 【解析】
在连接直线外一点与直线上各点的线段中,垂线段最短,所以码头应建在A点.故选A.
3.D 【解析】 由对顶角的定义,可知点A,B,C,N处各有2对对顶角,所以共有8对对顶角.故选D.
4.A 【解析】 根据同位角、内错角、同旁内角的定义,可知∠A与∠ABC是同旁内角,∠3与∠1是内错角,∠2与∠3是同位角,∠1与∠2既不是同位角、内错角,也不是同旁内角.故选A.
5.A 【解析】 B项,根据内错角相等,两直线平行,可判定l1∥l2;C项,根据同旁内角互补,两直线平行,可判定l1∥l2;D项,根据同位角相等,两直线平行,可判定l1∥l2.故选A.
6.C 【解析】 如图,过点E作EF∥AB,因为AB∥CD,所以AB∥CD∥EF,所以∠C=∠FEC,∠BAE=∠FEA.因为∠C=44°,∠AEC为直角,所以∠FEC=44°,∠BAE=∠AEF=90°-44°=46°,所以∠1=180°-∠BAE=180°-46°=134°.故选C.
7.D 【解析】 如图,因为DC∥FP,所以∠EFP=∠FED=32°.因为∠1=∠2,所以FP∥AB,所以∠GFP=∠AGF=76°,所以∠GFE=∠GFP+∠EFP=76°+32°=108°,又因为FH平分∠GFE,所以∠GFH=∠GFE=54°,所以∠PFH=∠GFP-∠GFH=76°-54°=22°.故选D.
8.B 【解析】 因为∠B=∠AGH,所以GH∥BC,所以∠1=∠HGM,因为∠1=∠2,所以∠2=∠HGM,所以DE∥GF,因为
GF⊥AB,所以HE⊥AB,故①④正确;因为GF∥DE,所以∠D=∠1,因为∠1=∠CMF,根据已知条件不能推出∠F=∠CMF,即不能推出∠D=∠F,故②错误;因为∠AHG=∠2+∠AHE,根据已知条件不能推出∠2=∠AHE,故③错误.综上,正确的有2个,故选B.
9.B 【解析】 由题图可知,长方形场地ABCD中去掉路后,草坪正好可以拼成一个新的长方形,且它的长为102-2=100(m),宽为51-1=50(m).所以草坪的面积为100×50=5
000(m2).故选B.
10.D 【解析】 如图,过点O作直线EF∥AB,则EF∥CD.因为AB∥EF,所以∠1=∠ABO=α.因为EF∥CD,所以∠DCO=∠2=β-α.故选D.
11.15 对顶角相等
12.∠FAD=∠EDA(答案不唯一) 【解析】 因为∠BAD=∠1+∠FAD,∠ADC=∠2+∠EDA,且∠BAD与∠ADC是内错角,如果∠BAD=∠ADC,那么AB∥CD,那么∠1+∠FAD=∠2+∠EDA,又因为∠1=∠2,所以∠FAD=∠EDA.
13.125° 【解析】 给各角标上序号,如图所示.因为∠1=∠2,∠2=∠5,所以∠1=∠5,所以l1∥l2,所以∠3+∠6=180°.因为∠3=55°,所以∠6=180°-55°=125°,所以∠4=∠6=125°.
14.50° 【解析】 因为∠1=70°,∠D=70°,所以∠1=∠D,所以AB∥CD,所以∠2+∠AEC=180°.又因为AE∥BC,所以∠C+∠AEC=180°,所以∠C=∠2=50°.
15.①②④ 【解析】
因为∠CAB=∠EAD=90°,∠1=∠CAB-∠2,∠3=∠EAD-∠2,所以∠1=∠3,故①正确;因为∠2=30°,所以∠1=90°-30°=60°,因为∠E=60°,所以∠1=∠E,所以AC∥DE,故②正确;因为∠2=30°,所以∠3=90°-30°=60°,因为∠B=45°,所以∠B≠∠3,所以BC与AD不平行,故③错误;由②得AC∥DE,所以∠4=∠C,故④正确.综上,正确的是①②④.
16.116° 【解析】 因为四边形ABCD为长方形,所以AD∥BC,所以∠1=∠DEG,∠DEF=∠EFG=58°.由折叠的性质,可得∠DEF=∠GEF=58°,所以∠1=∠DEG=∠GEF+∠DEF=116°.
17.【解析】 如图,因为AD⊥BC于点D,EF⊥BC于点F,
所以AD∥EF,所以∠1=∠3.
因为∠1=∠2,所以∠2=∠3,
所以DE∥AC.
18.【解析】 (1)三角形A'B'C'和三角形A″B″C″如图所示.
(2)由(1)中图形,知边AC所扫过的面积为12×2+5×1-×2×1=28.
19.【解析】
(1)因为∠AOC∶∠AOD=4∶5,
所以可设∠AOC=4x,∠AOD=5x,
则4x+5x=180°,解得x=20°,
所以∠AOC=80°,∠AOD=100°.
又因为OE平分∠BOD,∠BOD=∠AOC=80°,
所以∠EOD=∠BOE=40°,
所以∠COE=180°-40°=140°.
(2)因为OF⊥OE,所以∠FOE=90°,
所以∠FOD=50°,
所以∠COF=180°-50°=130°.
20.【解析】 (1)因为∠BAD+∠ADC=180°,
所以AB∥CD,所以∠DCG=∠B=87°.
(2)AD∥BC.理由如下:
因为AB∥CD,所以∠BAF=∠CFE,
又因为AE平分∠BAD,所以∠BAF=∠FAD,
所以∠DAF=∠CFE,
因为∠CFE=∠AEB,所以∠DAF=∠AEB,所以AD∥BC.
(3)当α=2β时,AE∥DG.理由如下:
若AE∥DG,则∠DGC=∠AEB=∠DAE=∠DAB,
即当α=2β时,AE∥DG.
21.【解析】 如图,延长CD交直线GF于点M.
因为CD∥EF,
所以∠M=∠EFG.
因为CH∥AB,所以∠HCB+∠ABC=180°,
因为∠EFG+∠BCD=∠ABC,
所以∠EFG+∠BCD+∠HCB=180°,
所以∠M+∠BCD+∠HCB=180°,
所以CH∥GF,所以AB∥GF.
22.【解析】 (1)如图1,过P作PE∥AB,
因为AB∥CD,
所以PE∥AB∥CD,
所以∠APE=∠BAP,∠CPE=∠DCP,
所以∠APC=∠APE+∠CPE=∠BAP+∠DCP=50°+30°=80°.
(2)∠AKC=∠APC.理由如下:
如图2,过K作KE∥AB,过P作PF∥AB.
因为AB∥CD,所以KE∥AB∥CD,
所以∠AKE=∠BAK,∠CKE=∠DCK,
所以∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
同理可得,∠APC=∠BAP+∠DCP,
因为∠BAP与∠DCP的角平分线相交于点K,
所以∠BAK+∠DCK=∠BAP+∠DCP=(∠BAP+∠DCP)=∠APC,
所以∠AKC=∠APC.
(3)∠AKC=∠APC.理由如下:
如图3,过K作KE∥AB,过P作PF∥AB.
因为AB∥CD,所以KE∥AB∥CD,
所以∠BAK=∠AKE,∠DCK=∠CKE,
所以∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,
同理可得,∠APC=∠BAP-∠DCP,
因为∠BAP与∠DCP的角平分线相交于点K,
所以∠BAK-∠DCK=∠BAP-∠DCP=(∠BAP-∠DCP)=∠APC,
所以∠AKC=∠APC.
