15.4.1提公因式法分解因式
文档属性
| 名称 | 15.4.1提公因式法分解因式 |  | |
| 格式 | rar | ||
| 文件大小 | 376.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-09 21:52:33 | ||
图片预览






文档简介
(共17张PPT)
探究1
※
※
※
请把35分解质因数
分解质因数与乘法什么关系
35=
互逆运算
探究2
※
※
※
请把下列多项式写成整式的乘积的形式:
(1) x2+x=
(2) x2-1=
x(x+1)
(x+1)(x-1)
计算
(1) x(x+1)=
(2)(x+1)(x-1)=
x2+x
x2-1
整式乘法
因式分解
也叫因式分解
象这样把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.
归纳
(1) x2+x= x(x+1)
(2) x2-1=(x+1)(x-1)
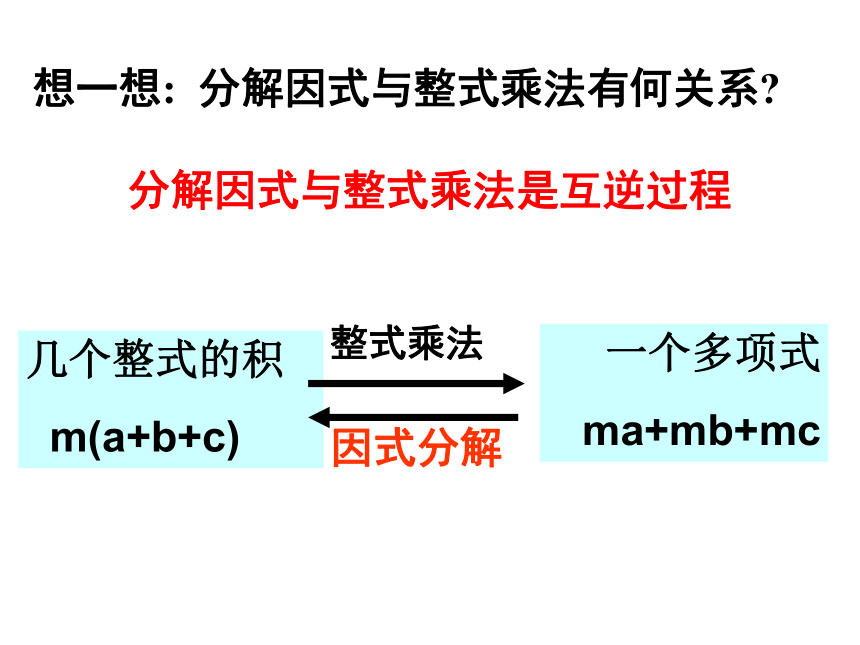
想一想: 分解因式与整式乘法有何关系
分解因式与整式乘法是互逆过程
几个整式的积
m(a+b+c)
一个多项式
ma+mb+mc
整式乘法
因式分解
判断下列各式是不是因式分解
(1) x2-4y2 =(x+2y)(x-2y)
是
(2) 3x2y3z =3xyz xy2
不是
不是
(4) m2-3m+1 =m(m-3)+1
不是
(3)
(5) (a-3)(a+3)=a2-9
不是
1、观察下列多项式有何共同特点?
ab +bc; 3x2+x; mb2+nb+b.
多项式各项都含有的相同因式,叫做这个多项式各项的公因式。
如:bx+ax的公因式是x.
议一议
多项式2x2+6x3,12a2b3-8a3b2-16ab4各项的公因式是什么?
系数:找各项系数的最大公约数。
字母:找各项的相同字母
指数:找各项相同字母的最低次幂
如何确定公因式?
请说出下列多项式的公因式
1、ma + mb 2、4kx - 8ky
3、5y3+20y2 4、a2b-2ab2+ab
5、 4x2-8ax+2x 6、3(a+b)2-6(a+b)3
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。
提公因式法:
提公因式法的一般步骤 :
1、确定提取的公因式
2、提取公因式
例1、
注意:多项式中,第三项是x,它的系数是1;它在因式分解时不能漏掉。
注意:如果多项式的第一项的系数是负的,一般要提出“-”号,使括号内的第一项的系数是正的,在提出“-”号时,多项式的各项都要变号。
练习: 1、把-4x2+8ax+2x 分解因式
2、把-3ab + 6abx - 9aby分解因式
请在下列各式等号右边的括号前填入“+”或“-”号,使等式成立:
(1) 2-a= ___ (a-2)
(2) b+a=___ (a+b)
(3) (b-a)2=___(a-b)2
(4) -m-n=___ (m+n)
(5) -s2+t2=___ (s2-t2)
_
+
+
_
_
括号前面是“+”号,括到括号里的各项都不变号;
括号前面是“-”号,括到括号里的各项都要变号。
n 为偶数:
(a-b)n =(b-a)n
n 为奇数:
(a-b)n=-(b-a)n
例4 把2a(b+c)-3(b+c)分解因式
例5、把6(x-2)+x(2-x)分解因式。
(1) a(x-y)+b(y-x)
(2) 6(m-n)3-12(n-m)2
练习:把下列各式分解因式:
(3) 2(a-b)2 - a+b
(4) 2(a-b)2 - (b-a)3
(1) 2x2+3x3+x=x(2x+3x2)
(2) 3a2c-6a3c=3a2(c-2ac)
(3) 3x2+6x-3=3x(x+2)-3
1.下面的因式分解对吗 如果不对,应怎样改正
不对. 2x2+3x3+x=x(2x+3x2+1)
不对.3a2c-6a3c=3a2c(1-2a)
不对. 3x2+6x-3=3(x2+2x-1)
2.利用因式分解进行计算
25×28 - 25×12 - 25×6
32006 - 5×32005 + 6×32004
小结:
今天我们学习了提取公因式法分解因式,可以用四句顺口溜来总结记忆用提取公因式法分解因式的技巧:
各项有“公”先提“公”,
首项有负常提负,
母项提出莫漏1,
括号里面分到“底”。
探究1
※
※
※
请把35分解质因数
分解质因数与乘法什么关系
35=
互逆运算
探究2
※
※
※
请把下列多项式写成整式的乘积的形式:
(1) x2+x=
(2) x2-1=
x(x+1)
(x+1)(x-1)
计算
(1) x(x+1)=
(2)(x+1)(x-1)=
x2+x
x2-1
整式乘法
因式分解
也叫因式分解
象这样把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.
归纳
(1) x2+x= x(x+1)
(2) x2-1=(x+1)(x-1)
想一想: 分解因式与整式乘法有何关系
分解因式与整式乘法是互逆过程
几个整式的积
m(a+b+c)
一个多项式
ma+mb+mc
整式乘法
因式分解
判断下列各式是不是因式分解
(1) x2-4y2 =(x+2y)(x-2y)
是
(2) 3x2y3z =3xyz xy2
不是
不是
(4) m2-3m+1 =m(m-3)+1
不是
(3)
(5) (a-3)(a+3)=a2-9
不是
1、观察下列多项式有何共同特点?
ab +bc; 3x2+x; mb2+nb+b.
多项式各项都含有的相同因式,叫做这个多项式各项的公因式。
如:bx+ax的公因式是x.
议一议
多项式2x2+6x3,12a2b3-8a3b2-16ab4各项的公因式是什么?
系数:找各项系数的最大公约数。
字母:找各项的相同字母
指数:找各项相同字母的最低次幂
如何确定公因式?
请说出下列多项式的公因式
1、ma + mb 2、4kx - 8ky
3、5y3+20y2 4、a2b-2ab2+ab
5、 4x2-8ax+2x 6、3(a+b)2-6(a+b)3
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。
提公因式法:
提公因式法的一般步骤 :
1、确定提取的公因式
2、提取公因式
例1、
注意:多项式中,第三项是x,它的系数是1;它在因式分解时不能漏掉。
注意:如果多项式的第一项的系数是负的,一般要提出“-”号,使括号内的第一项的系数是正的,在提出“-”号时,多项式的各项都要变号。
练习: 1、把-4x2+8ax+2x 分解因式
2、把-3ab + 6abx - 9aby分解因式
请在下列各式等号右边的括号前填入“+”或“-”号,使等式成立:
(1) 2-a= ___ (a-2)
(2) b+a=___ (a+b)
(3) (b-a)2=___(a-b)2
(4) -m-n=___ (m+n)
(5) -s2+t2=___ (s2-t2)
_
+
+
_
_
括号前面是“+”号,括到括号里的各项都不变号;
括号前面是“-”号,括到括号里的各项都要变号。
n 为偶数:
(a-b)n =(b-a)n
n 为奇数:
(a-b)n=-(b-a)n
例4 把2a(b+c)-3(b+c)分解因式
例5、把6(x-2)+x(2-x)分解因式。
(1) a(x-y)+b(y-x)
(2) 6(m-n)3-12(n-m)2
练习:把下列各式分解因式:
(3) 2(a-b)2 - a+b
(4) 2(a-b)2 - (b-a)3
(1) 2x2+3x3+x=x(2x+3x2)
(2) 3a2c-6a3c=3a2(c-2ac)
(3) 3x2+6x-3=3x(x+2)-3
1.下面的因式分解对吗 如果不对,应怎样改正
不对. 2x2+3x3+x=x(2x+3x2+1)
不对.3a2c-6a3c=3a2c(1-2a)
不对. 3x2+6x-3=3(x2+2x-1)
2.利用因式分解进行计算
25×28 - 25×12 - 25×6
32006 - 5×32005 + 6×32004
小结:
今天我们学习了提取公因式法分解因式,可以用四句顺口溜来总结记忆用提取公因式法分解因式的技巧:
各项有“公”先提“公”,
首项有负常提负,
母项提出莫漏1,
括号里面分到“底”。
