北师大九年级数学上册:相似的基本模型整理
文档属性
| 名称 | 北师大九年级数学上册:相似的基本模型整理 |
|
|
| 格式 | zip | ||
| 文件大小 | 181.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 00:00:00 | ||
图片预览


文档简介
相似的基本模型
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.。相似和勾股是产生等式的主要依据,其他依据还有面积法,三角函数等。因此要掌握相似三角形的基本图形,体会其各种演变和联系。现将基本模型总结如下:
模型一
A字型
模型分析
有一个公共角(∠A),此时需要找另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论。
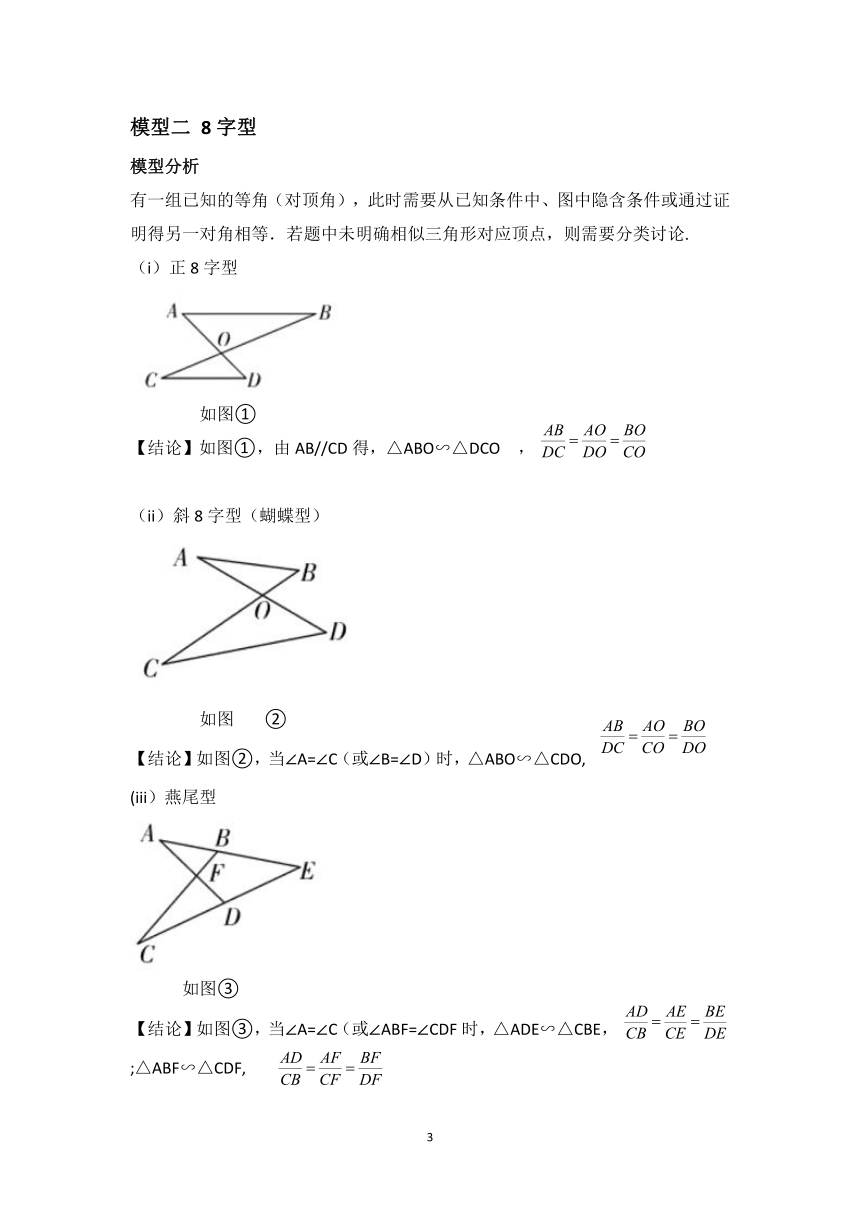
(i)正A字型(ii)反A共角型
图①图②图③
【结论】如图①,由DE//BC得,△ADE∽△ABC,
【结论】如图②,当∠AED=∠B(或∠ADE=∠C)时,△ADE∽△ACB,
如图③,∠C=∠ADE=90°,则△ADE∽△∠ACB,
(iii)反A共边共角型
图④图⑤(双垂直型(影射型))
【结论】如图④,当∠ACD=
∠B或∠ADC=∠ACB)时,△ADC∽△ACB,
AC2=
AD·AB;
如图⑤,CD⊥AB,AC⊥BC,则:
△CAD∽△BCD,CD2=AD·BD;
△CDA∽△BCA,AC2=AD:AB;
△BCD∽△BAC,BC2=BD·B4.
基本模型针对练
1.如图,在△ABC中,点D、E分别在AB、AC边上,DE//BC.若AD=1,BD=2,则
的值为()
B.
C.
D.
2;在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,
当AE=时,以A、D、E为顶点的三角形与△ABC相似.
3.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,E是AC上任意一点,连接
BE,过点A作AF⊥BE于点F.求证∶
BD·BC=BF·BE.
模型二
8字型
模型分析
有一组已知的等角(对顶角),此时需要从已知条件中、图中隐含条件或通过证明得另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论.
(i)正8字型
如图①
【结论】如图①,由AB//CD得,△ABO∽△DCO
,
(ii)斜8字型(蝴蝶型)
如图②
【结论】如图②,当∠A=∠C(或∠B=∠D)时,△ABO∽△CDO,
(iii)燕尾型
如图③
【结论】如图③,当∠A=∠C(或∠ABF=∠CDF时,△ADE∽△CBE,
;△ABF∽△CDF,
(iv)三平行型
如图④
【结论】如图④,由AB//EF//DC得,△AFB∽△CFD,
△CEF∽△CBA,,
△BEF∽△BCD,
针
对
训
练
如图,点E、F分别在菱形ABCD的边4B、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于点H,若则的值为
.
如图,在△ABC中,∠ABC=90°,∠C=30°,D为BC上一点,DE⊥AC于点E.
(1)求证∶
△ADC∽△BEC;
(2)若点D为BC的中点,AB=4,求BE的长.
模型三
一线三等角型(K型)
模型分析
两个相等的角的一边在同一条直线上,另一边在该直线的同侧或异侧,第三个与之相等的角的顶点在前一组等角的顶点所确定的线段上或线段的延长线上,该角的两边分别位于一直线的同侧或异侧,则此时直线同侧或异侧的两三角形相似.
点P在线段AB上(同侧型)
(2)点P在线段4B的延长线上(异侧型)
针
对训练
如图,在正方形ABCD中,点E、F、G分别在AB,BC,CD上,且∠EFG=90°.若
AB=12,AE=3,CF=4,则CG的长为
。
6题图
7题图
7.如图,在正方形ABCD中,AB=4,点E是DC延长线上的一点,连接BE,过点E作
EF⊥BE,与AD的延长线交于点F.若CE=2,则DF的长为
。
.
如图,在△ABC中,AB=AC,点D、P分别是边AC、BC上的点,且∠APD=∠B.求证∶
AC·CD=CP·BP.
综
合训练
如图①,在正方形ABCD中,E是边BC的中点,F是CD上一点,已知∠AEF=90°.(1)求证∶
EC/DF=2/3;
如图②,在平行四边形ABCD中,E是边BC上一点,F是边CD上一点,
∠AFE=∠D,∠AEF=90°.若∠AFE=45°,求EC/DF的值.
相似三角形是几何中重要的证明模型之一,是全等三角形的推广,分析图形间的关系离不开数量的计算.。相似和勾股是产生等式的主要依据,其他依据还有面积法,三角函数等。因此要掌握相似三角形的基本图形,体会其各种演变和联系。现将基本模型总结如下:
模型一
A字型
模型分析
有一个公共角(∠A),此时需要找另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论。
(i)正A字型(ii)反A共角型
图①图②图③
【结论】如图①,由DE//BC得,△ADE∽△ABC,
【结论】如图②,当∠AED=∠B(或∠ADE=∠C)时,△ADE∽△ACB,
如图③,∠C=∠ADE=90°,则△ADE∽△∠ACB,
(iii)反A共边共角型
图④图⑤(双垂直型(影射型))
【结论】如图④,当∠ACD=
∠B或∠ADC=∠ACB)时,△ADC∽△ACB,
AC2=
AD·AB;
如图⑤,CD⊥AB,AC⊥BC,则:
△CAD∽△BCD,CD2=AD·BD;
△CDA∽△BCA,AC2=AD:AB;
△BCD∽△BAC,BC2=BD·B4.
基本模型针对练
1.如图,在△ABC中,点D、E分别在AB、AC边上,DE//BC.若AD=1,BD=2,则
的值为()
B.
C.
D.
2;在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,
当AE=时,以A、D、E为顶点的三角形与△ABC相似.
3.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,E是AC上任意一点,连接
BE,过点A作AF⊥BE于点F.求证∶
BD·BC=BF·BE.
模型二
8字型
模型分析
有一组已知的等角(对顶角),此时需要从已知条件中、图中隐含条件或通过证明得另一对角相等.若题中未明确相似三角形对应顶点,则需要分类讨论.
(i)正8字型
如图①
【结论】如图①,由AB//CD得,△ABO∽△DCO
,
(ii)斜8字型(蝴蝶型)
如图②
【结论】如图②,当∠A=∠C(或∠B=∠D)时,△ABO∽△CDO,
(iii)燕尾型
如图③
【结论】如图③,当∠A=∠C(或∠ABF=∠CDF时,△ADE∽△CBE,
;△ABF∽△CDF,
(iv)三平行型
如图④
【结论】如图④,由AB//EF//DC得,△AFB∽△CFD,
△CEF∽△CBA,,
△BEF∽△BCD,
针
对
训
练
如图,点E、F分别在菱形ABCD的边4B、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于点H,若则的值为
.
如图,在△ABC中,∠ABC=90°,∠C=30°,D为BC上一点,DE⊥AC于点E.
(1)求证∶
△ADC∽△BEC;
(2)若点D为BC的中点,AB=4,求BE的长.
模型三
一线三等角型(K型)
模型分析
两个相等的角的一边在同一条直线上,另一边在该直线的同侧或异侧,第三个与之相等的角的顶点在前一组等角的顶点所确定的线段上或线段的延长线上,该角的两边分别位于一直线的同侧或异侧,则此时直线同侧或异侧的两三角形相似.
点P在线段AB上(同侧型)
(2)点P在线段4B的延长线上(异侧型)
针
对训练
如图,在正方形ABCD中,点E、F、G分别在AB,BC,CD上,且∠EFG=90°.若
AB=12,AE=3,CF=4,则CG的长为
。
6题图
7题图
7.如图,在正方形ABCD中,AB=4,点E是DC延长线上的一点,连接BE,过点E作
EF⊥BE,与AD的延长线交于点F.若CE=2,则DF的长为
。
.
如图,在△ABC中,AB=AC,点D、P分别是边AC、BC上的点,且∠APD=∠B.求证∶
AC·CD=CP·BP.
综
合训练
如图①,在正方形ABCD中,E是边BC的中点,F是CD上一点,已知∠AEF=90°.(1)求证∶
EC/DF=2/3;
如图②,在平行四边形ABCD中,E是边BC上一点,F是边CD上一点,
∠AFE=∠D,∠AEF=90°.若∠AFE=45°,求EC/DF的值.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
