人教版八上数学第十四章整式的乘法与因式分解复习(知识点、典型例题) 课件(共65张PPT)
文档属性
| 名称 | 人教版八上数学第十四章整式的乘法与因式分解复习(知识点、典型例题) 课件(共65张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 00:00:00 | ||
图片预览






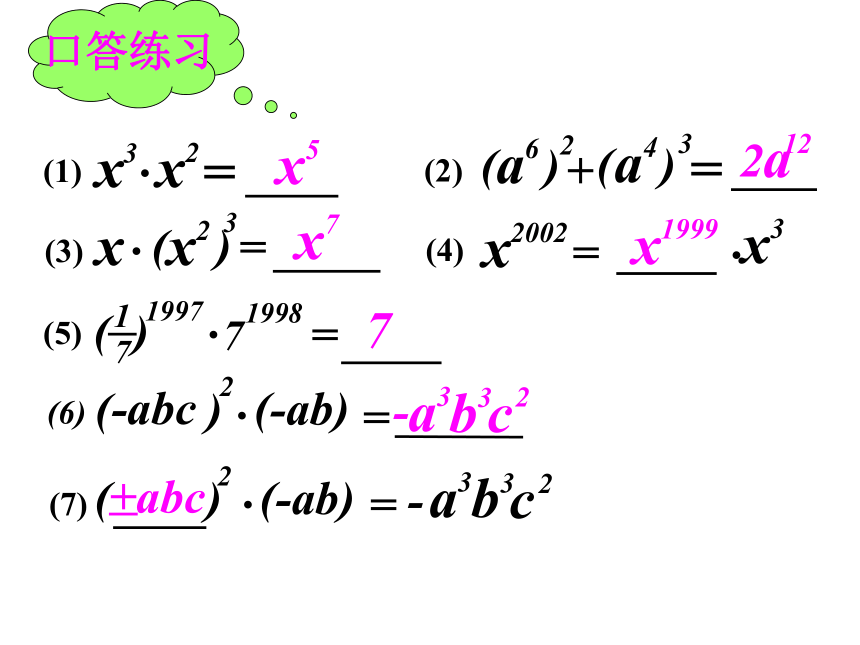




文档简介
(共65张PPT)
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
a
m
a
n
·
=
a
m+n
a
m
n
(
)
=
a
mn
ab
n
(
)
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3
)
=
[4
(
-3)]
a
3
a
2
(
)
x
2
x
5
(
)
b
=-12a
5
bx
7
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
单项式与多项式相乘
多项式的乘法
a
m
a
n
·
=
a
m+n
a
m
(
)
n
=
a
mn
ab
n
(
)
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3
)
m(a+b)=
(a+b)(m+n)=
ma+mb
am+an+bm+bn
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m
,
n都是正整数
想
一
想
a
2
a
3
a
5
+
=
(1)
a
2
a
a
2
·
=
(2)
(x-y)
2
(y-x)
5
=
(x-y)
7
(8)
x
2
(
)
3
=
x
5
(4)
a
3
x
6
3
5
-(x-y)
7
(y-x)
7
·
·
4
7
(6)
(-5)
(-5)
=5
11
-5
11
(-3)
2
·
3
3
=
(-3)
5
(7)
2
(5)
3
5a
·
2a
=10a
6
10a
5
(3)
a
3
a
3
=2a
3
a
6
找一找
4
7
-
x
2
y
z
2
(
)
7
4
-
x
y
2
(
)
=
x
3
y
3
10
5
10
3
-
10
2
10
10
(
)
(
)
-2
·
·
3
(
)
=
-6
2
1
-
6
1
-
a
2
b
3
a
8
b
27
(
)
3
=
a
3n
2
3n
(
)
·
b
2
(
)
ab
(
)
=
(A)
(D)
(B)
(C)
D
6n
口答练习
x
3
x
2
·
=
(
)
a
6
2
+
a
4
3
(
)
=
x
x
2
·
(
)
3
=
x
3
x
2002
·
=
·
=
7
1
(
)
1997
7
1998
2
=
·
(
)
(-ab)
-
c
2
b
3
a
3
(1)
(3)
(7)
·
-abc
(
)
(-ab)
2
=
(6)
(5)
(4)
(2)
x
5
2a
12
x
7
x
1999
7
-
a
3
b
3
c
2
+abc
比一比
算
计
(1)
3x
2
(
)
3
-
7x
3
[
]
x
3
-x
4x
2
+1
(
)
a
2
(
)
-2b
2
a+2b
(
)
-2ab(a-b)
(2)
先化简,再求值:
其中
a=1,b=
2
1
.
公
式
的
反
向
使
用
公
式
的
反
向
使
用
试用简便方法计算:
(ab)n
=
an·bn
(m,n都是正整数)
反向使用:
an·bn
=
(ab)n
(1)
23×53
;
(2)
(-5)16
×
(-2)15
(3)
24
×
44
×(-0.125)4
;
=
(2×5)3
=
103
=
(-5)×[(-5)×(-2)]15
=
-5×1015
=
[2×4×(-0.125)]4
=
14
=
1
(1)
(x5y)
÷
x2
=
x5
?
2
·y
(2)
(8m2n2)
÷
(2m2n)
=
(8÷2
)·m2
?
2·n2
?
1
;
(3)
(a4b
2c)
÷
(3a2b)
=
(1÷3
)·a4
?
2·b
2
?1·c
.
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷
(除式的系数)
写在商里面作
(被除式的指数)
—(除式的指数)
商式的系数=
单项式除以单项式,其结果(商式)仍是
被除式里单独有的幂,
(同底数幂)
商的指数=
一个单项式;
?
因式。
单项式
的
除法
法则
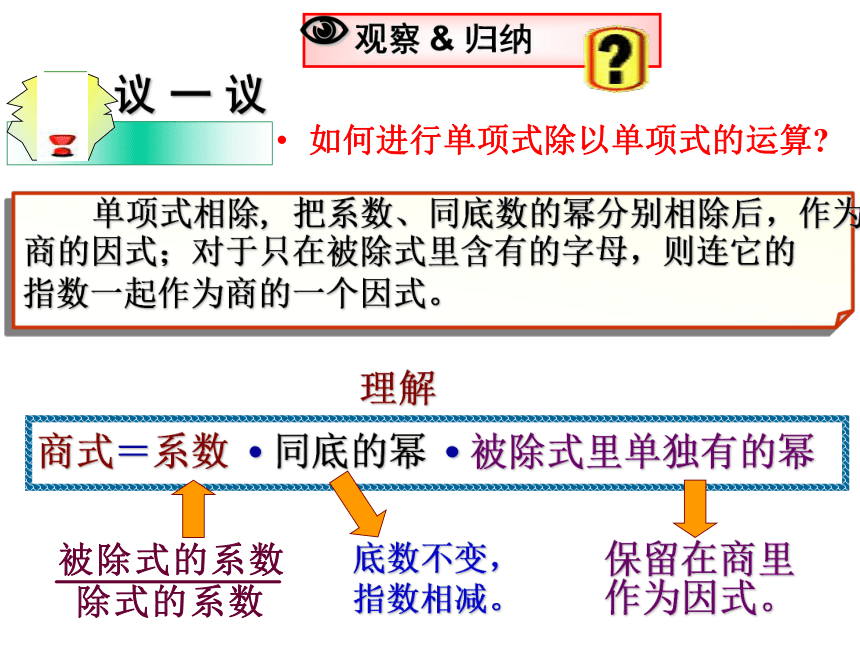
如何进行单项式除以单项式的运算?
议
一
议
单项式相除,
把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。
理解
商式=系数
?
同底的幂
?
被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
观察
&
归纳
?
解:
(1).(2x?y)?·(7xy?)÷(14x4y?)
=-56x7y5
÷(14x4y?)
=
-4x3y2
解:(2).(2a+b)4÷(2a+b)?
=(2a+b)?
=
4a2+4ab+b2
=8x6y3
·(7xy?)÷(14x4y?)
=
(2a+b)4-2
(1)(-a)8÷(-a2)
(2)-5a5b3c÷5a4b3
(4)-3a2x4y3÷(-axy2)
(5)(4×109)÷(-2×103)
=-a6
=-ac
=3ax3y
=-2×106
(3)
6m2n÷(-2mn)
=
-3m
你找到了
多项式除以单项式的规律
吗?
议一议
(
a+b+c
)÷m
=
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
多项式除以单项式的法则
例
题
解
析
例3
计算:
(2)原式=
?
例题
?
=
(1)(-2a4b3c)3÷(-8a4b5c)
(3
)(-3.6×1010)÷(-2×102)2÷(3×102)2
=a8b4c2
=
–10
(2)(6x2y3)2÷(3xy2)2
=4x2y2
乘法公式
平方差公式
完全平方公式(两数和的平方)
(a+b)(a-b)
=
a
2
b
2
-
(a+b)
2
=
a
2
b
2
2ab
+
+
二次三项型乘法公式
(x+a)(x+b)=
x
+(a+b)x+ab
2
计算:
(1)
(2x+3)(2x-3)
(2)
(-x+2)(-x-2)
(3)
(-2x+y)(2x+y)
(4)
(y-x)(-x-y)
(
5
)
1998×2002.
例1
计算
2018
2022
2018
2022
=
(2020-2)(2020+2)
=4080400-4
=4080396
解
想一想
下列计算是否正确?如不正确,应
如何改正?
(-x+6)(-x-6)
=
-
x
2
-
6
(1)
2
-x
-
1
(-x-1)(x+1)
=
(2)
=
(-x)
2
-
6
2
=
x
2
-
36
-(x+1)
=
(x+1)
=
-(x+1)
2
=
+
+
1
(
)
x
2
2x
-
=
-
x
2
-
2x
-1
(3)
(-2xy-1)(2xy-1)
=
1-2xy
2
=(-1)
2
-(2xy)
2
2
=1-4x
y
2
3
9
5
20x
2ab
4xy
已知
(a+b)
2
=
11,
(a-b)
2
=7,
则ab=(
)
(1)
(A)
1
(B)-1
(C)
0
(D)
1或-1
(C)
(D)
(2)
如果
4x
+12xy+k是一个关于x、y的完全
2
平方式,则k=(
)
(A)
(B)
3y
2
9y
2
y
36y
2
是一个关于x、y的完全平
如果4x
2
+kxy
+
9y
2
方式,则k=(
)
A
B
+
12
(3)如果a
+
a
1
=3,则
a
2
+
a
2
1
=(
)
(A)
7
(B)
9
(C)
10
(D)
11
所以
=9
a+
a
1
(
)
2
所以
a
+
a
1
=9
2
2
+
2
A
故
a
a
1
=7
2
+
2
因为
a+
a
1
=3
解:
(a-2b+3)(a+2b-3)的结果是(
)
(A)
2
2
a
+4b
+12b-9
(C)
2
2
a
+4b
-12b-9
(B)
a
2
-4b
2
-12b-9
(D)
a
2
-4b
2
+12b-9
D
(4)计算
=[a-(2b-3)][a+(2b-3)]
=a
2
-(2b-3)
2
=a
2
-(4b
-12b+9)
2
=
a
2
-4b
2
+12b-9
(a-2b+3)(a+2b-3)
解:
(1)
(x
-
)(x+
)(
+
)
(2)
(2x+1)(4
+1)(2x-1)(16
+1)
(3)
(x+2y-3)(x-2y+3)
(4)
如果(2a+2b+1)(2a+2b-1)=63,求a+b
的值。
因式分解
1.运用前两节所学的知识填空
1).m(a+b+c)=
.
2).(a+b)(a-b)=
.
3).(a+b)2=
.
2.试一试
填空:
1).ma+mb+mc=
m?(
)
2).a2-b2=(
)(
)
3).a2+2ab+b2=(
)2
ma+mb+mc
a2-b2
a2+2ab+b2
你能发现这两组等式之间的联系和区别吗?
a+b+c
(a+b)(a-b)
a+b
一般地,把一个多项式转化成几个整式的积的形式,叫做因式分解,有时我们也把这一过程叫做分解因式。
定义
理解概念
判断哪些是因式分解?
(1)
x2-4y2=(x+2y)(x-2y)
(2)
2x(x-3y)=2x2-6xy
(3)
(5a-1)2=25a2-10a+1
(4)
x2+4x+4=(x+2)2
(5)(a-3)(a+3)=a2-9
因式分解
整式乘法
整式乘法
因式分解
整式乘法
两者都不是
像(1)这种因式分解的方法叫提公因式法
像(2),(3)利用乘法公式对多项式进行因式分解的这种因式分解的方法就称为公式法.
1)
ma+mb+mc=m(
a+b+c
)
2)
a2-b2=(a+b)(a-b
)
a2+2ab+b2=(a+b)2
注意事项
1)
首选提公因式法,其次考虑公式法
2)两项考虑平方差法,三项考虑完全平方公式
3)因式分解要砌底
4)(可用整式的乘法检验)但不走回头路
找出下列各多项式中的公因式
找一找
公因式
系数
字母
3
5a
6a2b
各项系数的最大公约数
取每项中含有的相同字母
问:多项式中的公因式是如何确定的?
指数
相同字母的最低次幂
易
错
分
析
1、
把下列各式分解因式:
1)18-2b?
2)
x4
–1
1.选择题:
3)下列各式能用平方差公式分解因式的是(
)
4X?+y?
B.
4
x-
(-y)?
-4
X?-y?
D.
-
X?+
y?
4)
-4a?
+1分解因式的结果应是
(
)
-(4a+1)(4a-1)
B.
-(
2a
–1)(2a
–1)
-(2a
+1)(2a+1)
D.
-(2a+1)
(2a-1)
D
D
拓展提高
1.把下列多项式因式分解
1).
6x(a+2b)2-3x(a+2b)
2).
(b-a)2-2a+2b
3).
a(a-b)2+(b-a)3
提公因式法因式分解
1)
13.8×0.125+86.2×
2)
0.73×32-0.32×63
3)
33+112+66
巧计妙算
1
8
3.解方程:
(5x+3)(5x+6)-(5x+3)(5x+7)=0
(x-2004)2=(2004-x)(2005-x)
提公因式法因式分解
(
)
(
)
+
-
x2-16
练习:分解下列各式:
(1)x2-16
解:(1)
(2)9m2-4n2
x
x
4
4
(
)
(
)
+
-
a2
b2
-
a
a
b
b
(
)
(
)
+
-
=
……①
=x2
-
42
42
x2
=
(2)
9m2-4n2
3m
3m
(
)
(
)
+
-
a2
a
a
b
b
……②
=(3m)2
-
(2n)2
(2n)2
(3m)2
=
b2
-
=
2n
2n
平方差公式的应用题:
1、利用分解因式简便计算
(1)
652-642
(2)
5.42-4.62
(3)
(4)
解:652-642
=(65+64)(65-64)
=129×1
=129
解:5.42-4.62
=(5.4+4.6)(5.4-4.6)
=10×0.8
=8
答案:5
答案:28
提高题:
2、已知
,
,求(a+b)2-(a-b)2的值。
解:
(a+b)2-(a-b)2
=[(a+b)+(a-b)][(a+b)-(a-b)]
=2a·2b
=4ab
当
,
时,
原式=4×
×
=
3、求证:当n是整数时,两个连续奇数的平方差
(2n+1)2-(2n-1)2是8的倍数。
思考:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2+2ab+b2
=(a+b)2
a2-2ab+b2
=
(a-b)2
完全平方公式
a2+2ab+b2
=(a+b)2
a2-2ab+b2
=
(a-b)2
用他们可以把一个三项式分解因式的特点:
两项是两个数的平方
另一项是加上(或减去)这两个数积的两倍
完全平方例题讲解(1)
x2-4x+4
=x2-4x+22
=(x-2)2
a2
+2a+1
=
a2
+2·a·1
+12
=(a+1)2
a2+10a+25
=a2+2·a(
)+(
)2
=(a+
)2
5
5
5
X2+12ax+36a2
=X2+2·x·6a
+(6a)2
=(x+6a)2
小练习(2)
4a2+25b2-20ab
=(2a)2
-2·2a·5b
+(5b)2
=(2a-5b)2
-8x2y-2x3-8xy2
=-2x(x2+4xy+4y2)
=-2x(x+2y)2
动手做
已知x=a+2b,y=a-2b,
求:x
+xy+y
2
2
(1)
(2)
解方程:
2
(x+11)(x-12)=x
-100
1
、已知a+b=5
,ab=
-2,
求(1)
a2+b2
(2)a-b
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2-4ab
2、已知
求x2-2x-3的值
6.若(x-m)2=x2+8x+n,求mn的值
7.若9x2-mx+4是一个完全平方式,
求m的值
8.若(m+n)2=11,(m-n)2=7.求5mn的值
9.在整式4x2+1中加上一个单
项式使之成为完全平方式,
则应添
。
10.在整式
中加上一个单项式使之成为完全平方式,则应添
。
11.若(2m-3n)2=(2m+3n)2+A成立,
A应为
。
13.若x2+2mx+36是完全平方式,
求m的值
15.已知:a+b=5,ab=3,
求a2+b2的值
16.已知:a-b=3,a2+b2=17
求(a+b)2的值
17.已知:ab=12,a2+b2=25,
求(a-b)2的值
考查知识点:(当m,n是正整数时)
1、同底数幂的乘法:am
·
an
=
am+n
2、幂的乘方:
(am
)n
=
amn
3、积的乘方:
(ab)n
=
anbn
4、合并同类项:
计算:
x3(-x)5-(-x4)2-(-2x3)4
-(-x10)(-
x)2
解此类题应注意明确法则及
各自运算的特点,避免混淆
.
1、若10x=5,10y=4,求102x+3y+1
的值.
2、计算:0.251000×(-2)2001
注意点:
(1)指数:相加
底数相乘
转化
(2)指数:乘法
幂的乘方
转化
(3)底数:不同底数
同底数
转化
(2)
(1)0.12516·(-8)
17;
逆用公式
即
(3)已知2m=3,2n=5,
求23m+2n+2的值.
计算:
(-2a
2
+3a
+
1)
?(-
2a)3
5x(x2+2x
+1)
-
3(2x
+
3)(x
-
5)
(3)
(2m2
–
1)(m
–
4)
-2
(
m2
+
3)(2m
–
5)
注意点:
1、计算时应注意运算法则及运算顺序
2、在进行多项式乘法运算时,注意不要漏
乘,以及各项符号是否正确。
计算:
(1-x)(1+x)(1+x2)-(1-x2)2
(x2+32)2-(x+3)2(x-3)2
①(x+4y-6z)(x-4y+6z)
②(x-2y+3z)2
例1、已知:x2+y2+6x-8y+25=0,
求x,y的值;
1、已知x2-2mx+16
是完全平方式,则m=_____
4、如果(2a+2b+1)(2a+2b-1)=63,那么a+b=_____
2、已知x2-8x+m是完全平方式,则m=_____
3、已知x2-8x+m2是完全平方式,则m=_____
±4
16
±4
±4
-mx
±8
5.若
则m=(
)
A.
3
B.
-10
C.
-3
D.-5
A
观察:
……请你用正整数n的等式表示你发现的规律
___________________________________.
正整数n
观察下列各组数,
请用字母表示它们的规律
……
n是正整数
观察下列各组数,
请用字母表示它们的规律
……
n是正整数
设
(n为大于0的自然数).
探究an
是否为8的倍数,并用文字语言表述你所获得的结论;
两个连续奇数的平方差是8的倍数
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
a
m
a
n
·
=
a
m+n
a
m
n
(
)
=
a
mn
ab
n
(
)
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3
)
=
[4
(
-3)]
a
3
a
2
(
)
x
2
x
5
(
)
b
=-12a
5
bx
7
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
单项式与多项式相乘
多项式的乘法
a
m
a
n
·
=
a
m+n
a
m
(
)
n
=
a
mn
ab
n
(
)
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3
)
m(a+b)=
(a+b)(m+n)=
ma+mb
am+an+bm+bn
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m
,
n都是正整数
想
一
想
a
2
a
3
a
5
+
=
(1)
a
2
a
a
2
·
=
(2)
(x-y)
2
(y-x)
5
=
(x-y)
7
(8)
x
2
(
)
3
=
x
5
(4)
a
3
x
6
3
5
-(x-y)
7
(y-x)
7
·
·
4
7
(6)
(-5)
(-5)
=5
11
-5
11
(-3)
2
·
3
3
=
(-3)
5
(7)
2
(5)
3
5a
·
2a
=10a
6
10a
5
(3)
a
3
a
3
=2a
3
a
6
找一找
4
7
-
x
2
y
z
2
(
)
7
4
-
x
y
2
(
)
=
x
3
y
3
10
5
10
3
-
10
2
10
10
(
)
(
)
-2
·
·
3
(
)
=
-6
2
1
-
6
1
-
a
2
b
3
a
8
b
27
(
)
3
=
a
3n
2
3n
(
)
·
b
2
(
)
ab
(
)
=
(A)
(D)
(B)
(C)
D
6n
口答练习
x
3
x
2
·
=
(
)
a
6
2
+
a
4
3
(
)
=
x
x
2
·
(
)
3
=
x
3
x
2002
·
=
·
=
7
1
(
)
1997
7
1998
2
=
·
(
)
(-ab)
-
c
2
b
3
a
3
(1)
(3)
(7)
·
-abc
(
)
(-ab)
2
=
(6)
(5)
(4)
(2)
x
5
2a
12
x
7
x
1999
7
-
a
3
b
3
c
2
+abc
比一比
算
计
(1)
3x
2
(
)
3
-
7x
3
[
]
x
3
-x
4x
2
+1
(
)
a
2
(
)
-2b
2
a+2b
(
)
-2ab(a-b)
(2)
先化简,再求值:
其中
a=1,b=
2
1
.
公
式
的
反
向
使
用
公
式
的
反
向
使
用
试用简便方法计算:
(ab)n
=
an·bn
(m,n都是正整数)
反向使用:
an·bn
=
(ab)n
(1)
23×53
;
(2)
(-5)16
×
(-2)15
(3)
24
×
44
×(-0.125)4
;
=
(2×5)3
=
103
=
(-5)×[(-5)×(-2)]15
=
-5×1015
=
[2×4×(-0.125)]4
=
14
=
1
(1)
(x5y)
÷
x2
=
x5
?
2
·y
(2)
(8m2n2)
÷
(2m2n)
=
(8÷2
)·m2
?
2·n2
?
1
;
(3)
(a4b
2c)
÷
(3a2b)
=
(1÷3
)·a4
?
2·b
2
?1·c
.
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷
(除式的系数)
写在商里面作
(被除式的指数)
—(除式的指数)
商式的系数=
单项式除以单项式,其结果(商式)仍是
被除式里单独有的幂,
(同底数幂)
商的指数=
一个单项式;
?
因式。
单项式
的
除法
法则
如何进行单项式除以单项式的运算?
议
一
议
单项式相除,
把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。
理解
商式=系数
?
同底的幂
?
被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
观察
&
归纳
?
解:
(1).(2x?y)?·(7xy?)÷(14x4y?)
=-56x7y5
÷(14x4y?)
=
-4x3y2
解:(2).(2a+b)4÷(2a+b)?
=(2a+b)?
=
4a2+4ab+b2
=8x6y3
·(7xy?)÷(14x4y?)
=
(2a+b)4-2
(1)(-a)8÷(-a2)
(2)-5a5b3c÷5a4b3
(4)-3a2x4y3÷(-axy2)
(5)(4×109)÷(-2×103)
=-a6
=-ac
=3ax3y
=-2×106
(3)
6m2n÷(-2mn)
=
-3m
你找到了
多项式除以单项式的规律
吗?
议一议
(
a+b+c
)÷m
=
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
多项式除以单项式的法则
例
题
解
析
例3
计算:
(2)原式=
?
例题
?
=
(1)(-2a4b3c)3÷(-8a4b5c)
(3
)(-3.6×1010)÷(-2×102)2÷(3×102)2
=a8b4c2
=
–10
(2)(6x2y3)2÷(3xy2)2
=4x2y2
乘法公式
平方差公式
完全平方公式(两数和的平方)
(a+b)(a-b)
=
a
2
b
2
-
(a+b)
2
=
a
2
b
2
2ab
+
+
二次三项型乘法公式
(x+a)(x+b)=
x
+(a+b)x+ab
2
计算:
(1)
(2x+3)(2x-3)
(2)
(-x+2)(-x-2)
(3)
(-2x+y)(2x+y)
(4)
(y-x)(-x-y)
(
5
)
1998×2002.
例1
计算
2018
2022
2018
2022
=
(2020-2)(2020+2)
=4080400-4
=4080396
解
想一想
下列计算是否正确?如不正确,应
如何改正?
(-x+6)(-x-6)
=
-
x
2
-
6
(1)
2
-x
-
1
(-x-1)(x+1)
=
(2)
=
(-x)
2
-
6
2
=
x
2
-
36
-(x+1)
=
(x+1)
=
-(x+1)
2
=
+
+
1
(
)
x
2
2x
-
=
-
x
2
-
2x
-1
(3)
(-2xy-1)(2xy-1)
=
1-2xy
2
=(-1)
2
-(2xy)
2
2
=1-4x
y
2
3
9
5
20x
2ab
4xy
已知
(a+b)
2
=
11,
(a-b)
2
=7,
则ab=(
)
(1)
(A)
1
(B)-1
(C)
0
(D)
1或-1
(C)
(D)
(2)
如果
4x
+12xy+k是一个关于x、y的完全
2
平方式,则k=(
)
(A)
(B)
3y
2
9y
2
y
36y
2
是一个关于x、y的完全平
如果4x
2
+kxy
+
9y
2
方式,则k=(
)
A
B
+
12
(3)如果a
+
a
1
=3,则
a
2
+
a
2
1
=(
)
(A)
7
(B)
9
(C)
10
(D)
11
所以
=9
a+
a
1
(
)
2
所以
a
+
a
1
=9
2
2
+
2
A
故
a
a
1
=7
2
+
2
因为
a+
a
1
=3
解:
(a-2b+3)(a+2b-3)的结果是(
)
(A)
2
2
a
+4b
+12b-9
(C)
2
2
a
+4b
-12b-9
(B)
a
2
-4b
2
-12b-9
(D)
a
2
-4b
2
+12b-9
D
(4)计算
=[a-(2b-3)][a+(2b-3)]
=a
2
-(2b-3)
2
=a
2
-(4b
-12b+9)
2
=
a
2
-4b
2
+12b-9
(a-2b+3)(a+2b-3)
解:
(1)
(x
-
)(x+
)(
+
)
(2)
(2x+1)(4
+1)(2x-1)(16
+1)
(3)
(x+2y-3)(x-2y+3)
(4)
如果(2a+2b+1)(2a+2b-1)=63,求a+b
的值。
因式分解
1.运用前两节所学的知识填空
1).m(a+b+c)=
.
2).(a+b)(a-b)=
.
3).(a+b)2=
.
2.试一试
填空:
1).ma+mb+mc=
m?(
)
2).a2-b2=(
)(
)
3).a2+2ab+b2=(
)2
ma+mb+mc
a2-b2
a2+2ab+b2
你能发现这两组等式之间的联系和区别吗?
a+b+c
(a+b)(a-b)
a+b
一般地,把一个多项式转化成几个整式的积的形式,叫做因式分解,有时我们也把这一过程叫做分解因式。
定义
理解概念
判断哪些是因式分解?
(1)
x2-4y2=(x+2y)(x-2y)
(2)
2x(x-3y)=2x2-6xy
(3)
(5a-1)2=25a2-10a+1
(4)
x2+4x+4=(x+2)2
(5)(a-3)(a+3)=a2-9
因式分解
整式乘法
整式乘法
因式分解
整式乘法
两者都不是
像(1)这种因式分解的方法叫提公因式法
像(2),(3)利用乘法公式对多项式进行因式分解的这种因式分解的方法就称为公式法.
1)
ma+mb+mc=m(
a+b+c
)
2)
a2-b2=(a+b)(a-b
)
a2+2ab+b2=(a+b)2
注意事项
1)
首选提公因式法,其次考虑公式法
2)两项考虑平方差法,三项考虑完全平方公式
3)因式分解要砌底
4)(可用整式的乘法检验)但不走回头路
找出下列各多项式中的公因式
找一找
公因式
系数
字母
3
5a
6a2b
各项系数的最大公约数
取每项中含有的相同字母
问:多项式中的公因式是如何确定的?
指数
相同字母的最低次幂
易
错
分
析
1、
把下列各式分解因式:
1)18-2b?
2)
x4
–1
1.选择题:
3)下列各式能用平方差公式分解因式的是(
)
4X?+y?
B.
4
x-
(-y)?
-4
X?-y?
D.
-
X?+
y?
4)
-4a?
+1分解因式的结果应是
(
)
-(4a+1)(4a-1)
B.
-(
2a
–1)(2a
–1)
-(2a
+1)(2a+1)
D.
-(2a+1)
(2a-1)
D
D
拓展提高
1.把下列多项式因式分解
1).
6x(a+2b)2-3x(a+2b)
2).
(b-a)2-2a+2b
3).
a(a-b)2+(b-a)3
提公因式法因式分解
1)
13.8×0.125+86.2×
2)
0.73×32-0.32×63
3)
33+112+66
巧计妙算
1
8
3.解方程:
(5x+3)(5x+6)-(5x+3)(5x+7)=0
(x-2004)2=(2004-x)(2005-x)
提公因式法因式分解
(
)
(
)
+
-
x2-16
练习:分解下列各式:
(1)x2-16
解:(1)
(2)9m2-4n2
x
x
4
4
(
)
(
)
+
-
a2
b2
-
a
a
b
b
(
)
(
)
+
-
=
……①
=x2
-
42
42
x2
=
(2)
9m2-4n2
3m
3m
(
)
(
)
+
-
a2
a
a
b
b
……②
=(3m)2
-
(2n)2
(2n)2
(3m)2
=
b2
-
=
2n
2n
平方差公式的应用题:
1、利用分解因式简便计算
(1)
652-642
(2)
5.42-4.62
(3)
(4)
解:652-642
=(65+64)(65-64)
=129×1
=129
解:5.42-4.62
=(5.4+4.6)(5.4-4.6)
=10×0.8
=8
答案:5
答案:28
提高题:
2、已知
,
,求(a+b)2-(a-b)2的值。
解:
(a+b)2-(a-b)2
=[(a+b)+(a-b)][(a+b)-(a-b)]
=2a·2b
=4ab
当
,
时,
原式=4×
×
=
3、求证:当n是整数时,两个连续奇数的平方差
(2n+1)2-(2n-1)2是8的倍数。
思考:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2+2ab+b2
=(a+b)2
a2-2ab+b2
=
(a-b)2
完全平方公式
a2+2ab+b2
=(a+b)2
a2-2ab+b2
=
(a-b)2
用他们可以把一个三项式分解因式的特点:
两项是两个数的平方
另一项是加上(或减去)这两个数积的两倍
完全平方例题讲解(1)
x2-4x+4
=x2-4x+22
=(x-2)2
a2
+2a+1
=
a2
+2·a·1
+12
=(a+1)2
a2+10a+25
=a2+2·a(
)+(
)2
=(a+
)2
5
5
5
X2+12ax+36a2
=X2+2·x·6a
+(6a)2
=(x+6a)2
小练习(2)
4a2+25b2-20ab
=(2a)2
-2·2a·5b
+(5b)2
=(2a-5b)2
-8x2y-2x3-8xy2
=-2x(x2+4xy+4y2)
=-2x(x+2y)2
动手做
已知x=a+2b,y=a-2b,
求:x
+xy+y
2
2
(1)
(2)
解方程:
2
(x+11)(x-12)=x
-100
1
、已知a+b=5
,ab=
-2,
求(1)
a2+b2
(2)a-b
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2-4ab
2、已知
求x2-2x-3的值
6.若(x-m)2=x2+8x+n,求mn的值
7.若9x2-mx+4是一个完全平方式,
求m的值
8.若(m+n)2=11,(m-n)2=7.求5mn的值
9.在整式4x2+1中加上一个单
项式使之成为完全平方式,
则应添
。
10.在整式
中加上一个单项式使之成为完全平方式,则应添
。
11.若(2m-3n)2=(2m+3n)2+A成立,
A应为
。
13.若x2+2mx+36是完全平方式,
求m的值
15.已知:a+b=5,ab=3,
求a2+b2的值
16.已知:a-b=3,a2+b2=17
求(a+b)2的值
17.已知:ab=12,a2+b2=25,
求(a-b)2的值
考查知识点:(当m,n是正整数时)
1、同底数幂的乘法:am
·
an
=
am+n
2、幂的乘方:
(am
)n
=
amn
3、积的乘方:
(ab)n
=
anbn
4、合并同类项:
计算:
x3(-x)5-(-x4)2-(-2x3)4
-(-x10)(-
x)2
解此类题应注意明确法则及
各自运算的特点,避免混淆
.
1、若10x=5,10y=4,求102x+3y+1
的值.
2、计算:0.251000×(-2)2001
注意点:
(1)指数:相加
底数相乘
转化
(2)指数:乘法
幂的乘方
转化
(3)底数:不同底数
同底数
转化
(2)
(1)0.12516·(-8)
17;
逆用公式
即
(3)已知2m=3,2n=5,
求23m+2n+2的值.
计算:
(-2a
2
+3a
+
1)
?(-
2a)3
5x(x2+2x
+1)
-
3(2x
+
3)(x
-
5)
(3)
(2m2
–
1)(m
–
4)
-2
(
m2
+
3)(2m
–
5)
注意点:
1、计算时应注意运算法则及运算顺序
2、在进行多项式乘法运算时,注意不要漏
乘,以及各项符号是否正确。
计算:
(1-x)(1+x)(1+x2)-(1-x2)2
(x2+32)2-(x+3)2(x-3)2
①(x+4y-6z)(x-4y+6z)
②(x-2y+3z)2
例1、已知:x2+y2+6x-8y+25=0,
求x,y的值;
1、已知x2-2mx+16
是完全平方式,则m=_____
4、如果(2a+2b+1)(2a+2b-1)=63,那么a+b=_____
2、已知x2-8x+m是完全平方式,则m=_____
3、已知x2-8x+m2是完全平方式,则m=_____
±4
16
±4
±4
-mx
±8
5.若
则m=(
)
A.
3
B.
-10
C.
-3
D.-5
A
观察:
……请你用正整数n的等式表示你发现的规律
___________________________________.
正整数n
观察下列各组数,
请用字母表示它们的规律
……
n是正整数
观察下列各组数,
请用字母表示它们的规律
……
n是正整数
设
(n为大于0的自然数).
探究an
是否为8的倍数,并用文字语言表述你所获得的结论;
两个连续奇数的平方差是8的倍数
