人教版 八年级数学下册 第18章 平行四边形 单元测试(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学下册 第18章 平行四边形 单元测试(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 403.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 00:00:00 | ||
图片预览


文档简介
人教版
八年级数学
第18章
平行四边形
一、选择题
1.
如图,在平行四边形中,,,平分交边于点,则线段,的长度分别为(
)
A.和
B.和
C.和
D.和如图
2.
(2020·荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为(
)
A.20
B.30
C.40
D.50
3.
点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有(
)种
A.
B.
C.
D.
4.
关于?ABCD的叙述,正确的是( )
A.
若AB⊥BC,则?ABCD是菱形
B.
若AC⊥BD,则?ABCD是正方形
C.
若AC=BD,则?ABCD是矩形
D.
若AB=AD,则?ABCD是正方形
5.
(2020·广州)如图5,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
图5
A.
B.
C.
D.
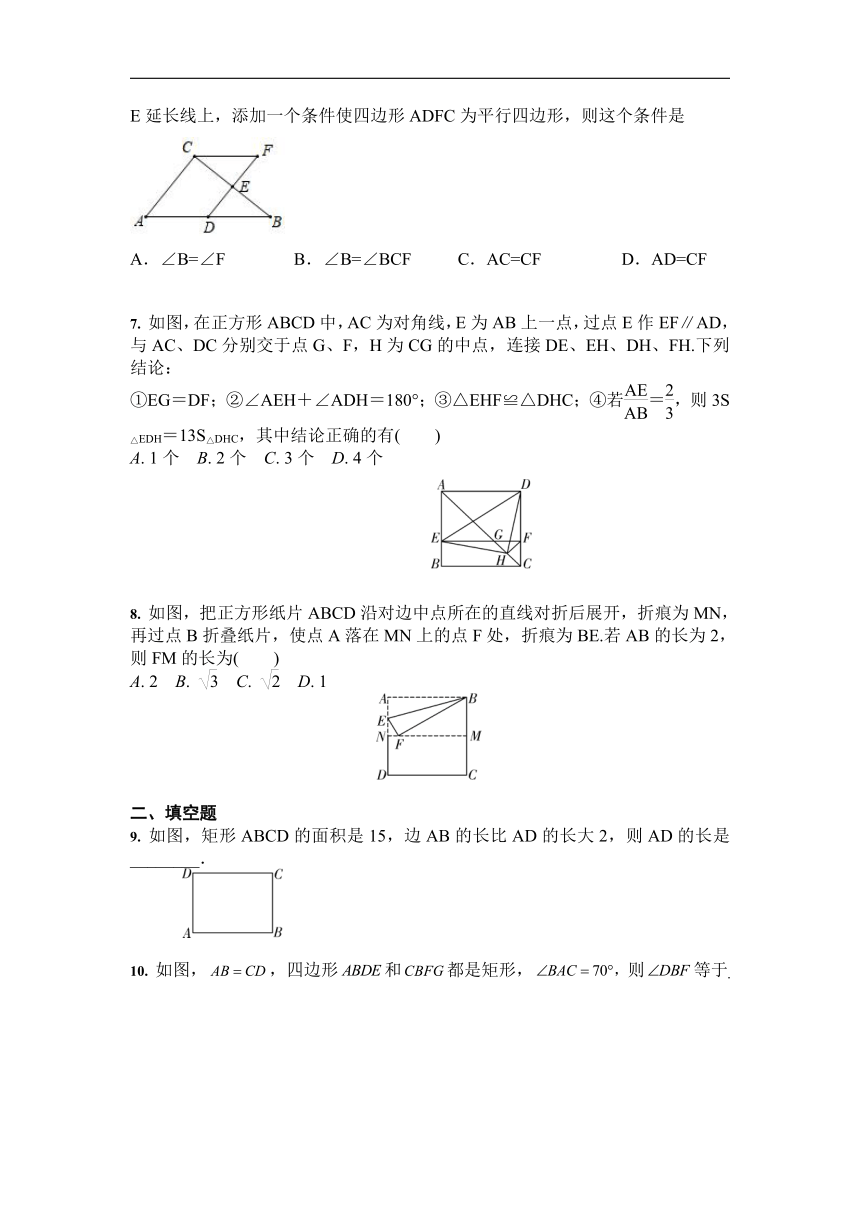
6.
(2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
7.
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH=13S△DHC,其中结论正确的有( )
A.
1个
B.
2个
C.
3个
D.
4个
8.
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A.
2
B.
C.
D.
1
二、填空题
9.
如图,矩形ABCD的面积是15,边AB的长比AD的长大2,则AD的长是________.
10.
如图,,四边形和都是矩形,则等于
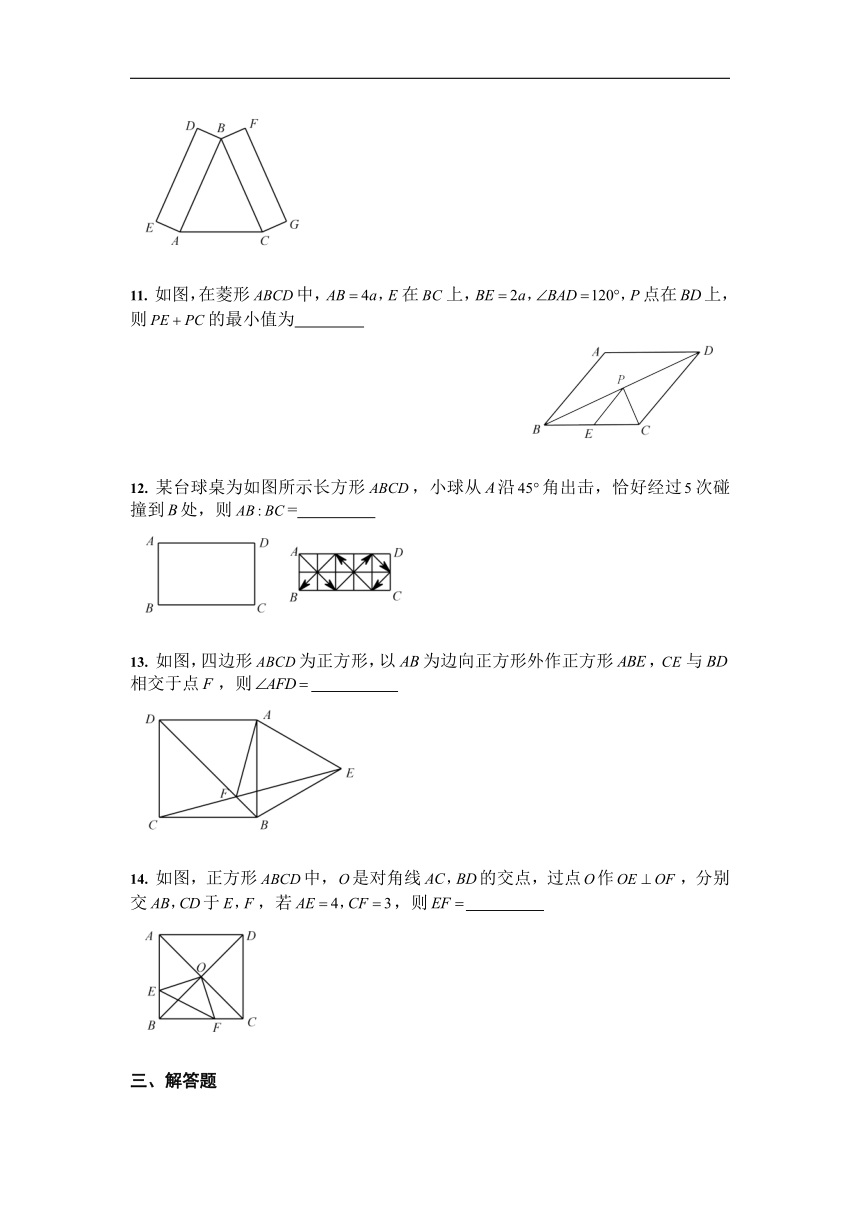
11.
如图,在菱形中,在上,点在上,则的最小值为
12.
某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
13.
如图,四边形为正方形,以为边向正方形外作正方形,与相交于点,则
14.
如图,正方形中,是对角线的交点,过点作,分别交于,若,则
三、解答题
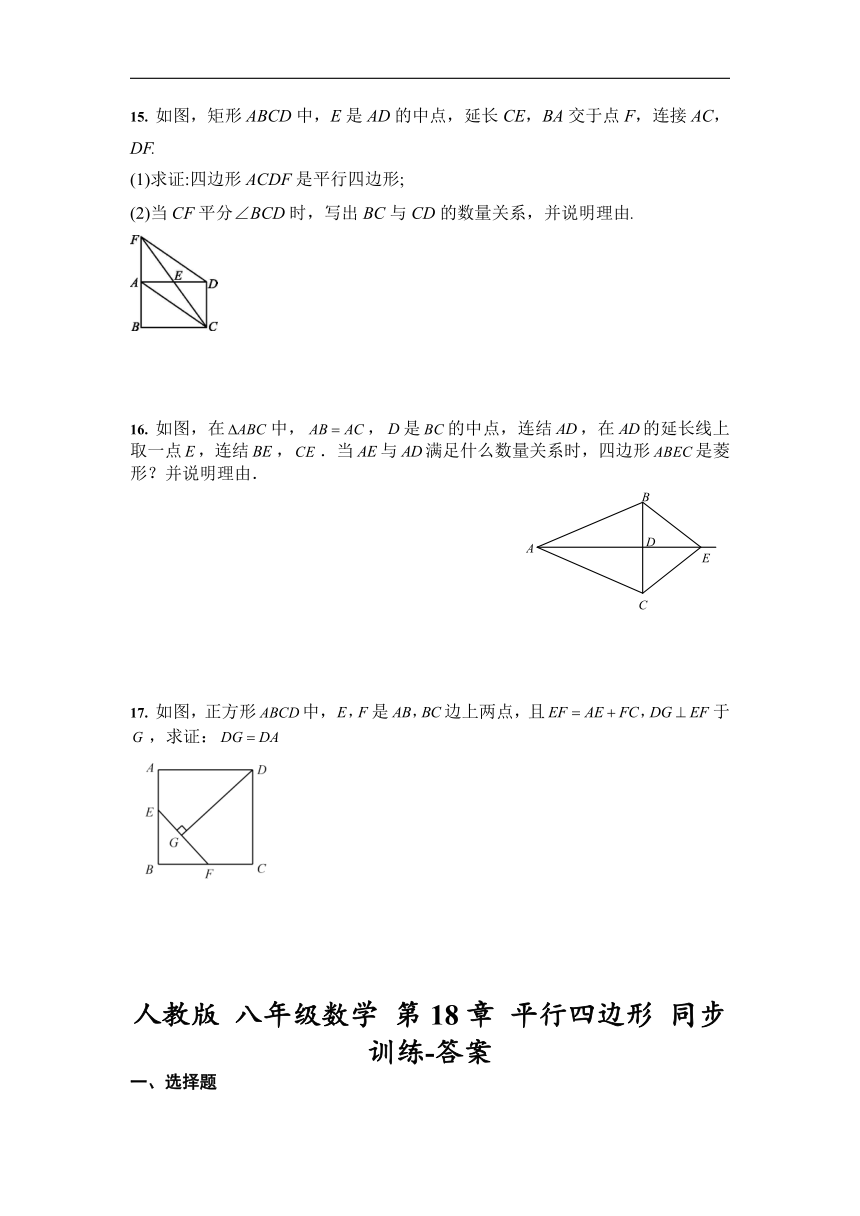
15.
如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
16.
如图,在中,,是的中点,连结,在的延长线上取一点,连结,.当与满足什么数量关系时,四边形是菱形?并说明理由.?
17.
如图,正方形中,是边上两点,且于,求证:
人教版
八年级数学
第18章
平行四边形
同步训练-答案
一、选择题
1.
【答案】B
2.
【答案】C
【解析】∵E,F分别是AD,BD的中点,∴EF是△DAB的中位线.∴AB=2EF=10.∵菱形的四边相等,∴菱形ABCD的周长=4AB=40.故选C.
3.
【答案】B
4.
【答案】C 【解析】逐项分析如下表:
选项
逐项分析
正误
A
有一个角是直角的平行四边形是矩形,不是菱形
×
B
对角线互相垂直的平行四边形是菱形,不一定是正方形
×
C
对角线相等的平行四边形是矩形
√
D
有一组邻边相等的平行四边形是菱形,不一定是正方形
×
5.
【答案】C
【解析】本题考查了矩形的性质,由勾股定理可得AC=10,再由矩形的对角线相等且互相平分的性质可得,OA=OD=5.
△ABD的面积为24,OA为△ABD
的中线,由中线等分面积可得,△AOD的面积为12.再由等面积法即可得OE+EF的值.过程如下:
∵
∴
即,∴OE+EF=,因此本题选C.
6.
【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7.
【答案】D 【解析】逐项分析如下表:
序号
逐项分析
正误
①
在正方形ABCD中,AB=BC=CD=DA,∠DAB=∠B=∠BCD=∠CDA=90°,∠ACB=∠ACD=45°,∵EF∥AD,∴四边形EFDA、四边形EFCB是矩形,∴∠EFC=∠ADC=90°,EF=DC,在Rt△CGF中,∠ACD=45°,∴GF=CF,∴EF-GF=CD-CF,即EG=DF
√
②
∵△GFC是等腰直角三角形,H是CG的中点,∴GH=FH,∠HGF=∠GFH=45°,∴∠EGH=∠DFH=135°,又由①知EG=DF,∴△EGH≌△DFH(SAS),∴∠HEF=∠FDH,∵∠AEH=∠AEF+∠HEF=90°+∠HEF,∠ADH=∠ADC-∠FDH=90°-∠FDH,∴∠AEH+∠ADH=180°
√
③
由②可知EH=DH,FH=CH,又∵EF=DC,∴△EHF≌△DHC(SSS)
√
④
∵△EGH≌△DFH,∴EH=DH,∠EHG=∠DHF,∴∠EHG+∠AHD=∠DHF+∠AHD=90°,即∠EHD=∠AHF=90°,∴△EHD为等腰直角三角形,∵=,∴设AE=2x,AB=3x,则DE==x,∴EH=DH=×x=x,∴S△EDH=EH2=×x2=x2.
在△DHC中,设CD边上的高为h,则h=CF=,则S△DHC=CD·h=×3x×=x2,==,即3S△EDH=13S△DHC
√
8.
【答案】B 【解析】∵AB=2,∴BF=2,又∵BM=BC=1,由勾股定理得FM==.
二、填空题
9.
【答案】3 【解析】本题主要考查了一元二次方程的实际应用问题.
设AD=x,由题知,AB=x+2,又∵矩形ABCD的面积为15,则x(x+2)=15,得到x2+2x-15=0,解得,x1=-5(舍)
,
x2=3,∴AD=3.
10.
【答案】
11.
【答案】
【解析】关于对称,连交于,且
为最小值
12.
【答案】
【解析】由图形可知:可推出
13.
【答案】
【解析】,故
14.
【答案】
三、解答题
15.
【答案】
解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,∴∠FAE=∠CDE,
∵E是AD的中点,∴AE=DE,
又∵∠FEA=∠CED,∴△FAE≌△CDE,∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形.
(2)BC=2CD.理由:
∵CF平分∠BCD,∴∠DCE=45°,
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,∴AD=2CD,
∵AD=BC,∴BC=2CD.
16.
【答案】
当(或或)时,四边形是菱形
理由如下:?
∵,∴
又点为中点,∴
∴四边形为平行四形边
∵
∴四边形为菱形
17.
【答案】
延长至点,使连结,由,得,进而推证,
18.2 特殊的平行四边形
一、选择题
1.已知矩形ABCD的对角线AC,BD相交于点O,
∠ADB=30°,AB=2,则OC的长是(
)
(A)1
(B)2
(C)4
(D)2
2.下列说法中正确的是(
)
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
3.如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是(
)
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
(A)①②
(B)①④
(C)①③④
(D)②③④
4.一个菱形的周长是20
cm,两条对角线的比是4∶3,则这个菱形的面积是(
)
(A)12
cm2
(B)96
cm2
(C)48
cm2
(D)24
cm2
5.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,则∠EBF的度数是(
)
A.75°
B.60°
C.50°
D.45°
6.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是(
)
(A)15
(B)16
(C)19
(D)20
7.已知?ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是(
)
A.∠BAC=∠DCA
B.∠BAC=∠DAC
C.∠BAC=∠ABD
D.∠BAC=∠ADB
8.平行四边形、矩形、菱形、正方形共有的性质是(
)
(A)对角线相等
(B)对角线互相平分
(C)对角线互相垂直
(D)对角线互相垂直平分
9.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是(
)
A.8
B.6
C.4
D.2
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分
△AFC的面积为( )
(A)12
(B)10
(C)8
(D)6
二、填空题
11.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,
P,Q分别为AO,AD的中点,则PQ的长度为 .?
12.菱形ABCD的对角线分别为18
cm与12
cm,则此菱形的面积为
cm2.
13.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),
(-2,0),点D在y轴上,则点C的坐标是 .?
14.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是 .?
15.如图,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,AC=BD.试添加一个条件
,使四边形ABCD为矩形.
16.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .?
解答题
17.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足
为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
18.如图,在菱形ABCD中,点E,O,F分别是边AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.
19.如图,在?ABCD中,O为AC的中点,过点O作EF⊥AC与边AD,BC分别相交于点E,F,求证:四边形AECF是菱形.
20如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
参考答案
一、选择题
1.已知矩形ABCD的对角线AC,BD相交于点O,
∠ADB=30°,AB=2,则OC的长是( B )
(A)1
(B)2
(C)4
(D)2
2.下列说法中正确的是(D)
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
3.如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( B )
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
(A)①②
(B)①④
(C)①③④
(D)②③④
4.一个菱形的周长是20
cm,两条对角线的比是4∶3,则这个菱形的面积是( D )
(A)12
cm2
(B)96
cm2
(C)48
cm2
(D)24
cm2
5.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,则∠EBF的度数是(B)
A.75°
B.60°
C.50°
D.45°
6.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( A )
(A)15
(B)16
(C)19
(D)20
7.已知?ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是(C)
A.∠BAC=∠DCA
B.∠BAC=∠DAC
C.∠BAC=∠ABD
D.∠BAC=∠ADB
8.平行四边形、矩形、菱形、正方形共有的性质是( B )
(A)对角线相等
(B)对角线互相平分
(C)对角线互相垂直
(D)对角线互相垂直平分
9.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是(C)
A.8
B.6
C.4
D.2
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分
△AFC的面积为( B )
(A)12
(B)10
(C)8
(D)6
二、填空题
11.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,
P,Q分别为AO,AD的中点,则PQ的长度为 2.5 .?
12.菱形ABCD的对角线分别为18
cm与12
cm,则此菱形的面积为108__cm2.
13.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),
(-2,0),点D在y轴上,则点C的坐标是 (-5,4) .?
14.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是 ①②③④ .?
15.如图,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,AC=BD.试添加一个条件答案不唯一,如:AB∥CD,使四边形ABCD为矩形.
16.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 (-1,5) .?
解答题
17.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足
为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
(1)证明:在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
又∵AD=EA,
∴△ADF≌△EAB,
∴DF=AB.
(2)解:∵∠ADF+∠FDC=90°,
∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.
18.如图,在菱形ABCD中,点E,O,F分别是边AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.
解:(1)证明:∵四边形ABCD为菱形,
∴AB=BC=CD=DA,
∠B=∠D.
又∵E,F分别是AB,AD的中点,
∴BE=DF.
∴△BCE≌△DCF(SAS).
(2)若AB⊥BC,则四边形AEOF为正方形,理由如下:
∵E,O分别是AB,AC的中点,∴EO∥BC.
又BC∥AD,∴OE∥AD.∴OE∥AF.
同理可证OF∥AE,
∴四边形AEOF为平行四边形.
由(1)可得AE=AF,
∴四边形AEOF为菱形.
∵AB⊥BC,∴∠BAD=90
°.
∴菱形AEOF为正方形.
19.如图,在?ABCD中,O为AC的中点,过点O作EF⊥AC与边AD,BC分别相交于点E,F,求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD.
∴AE∥CF.
∴∠OAE=∠OCF.
∵点O是AC的中点,∴OA=OC.
在△AOE和△COF中,
∴△AOE≌△COF(ASA).
∴AE=CF.
又∵AE∥CF,
∴四边形AECF是平行四边形.
∵EF与AC垂直,
∴四边形AECF是菱形.
20如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
解:∵四边形ABCD是菱形,BD=4,
∴OA=OC=AC,OB=OD=BD=2,AC⊥BD.
∵在Rt△OCD中,∠ACD=30
°,
∴CD=2OD=4,
OC===2.
∴AC=2OC=4.
∴S菱形ABCD=AC·BD=×4×4=8.
八年级数学
第18章
平行四边形
一、选择题
1.
如图,在平行四边形中,,,平分交边于点,则线段,的长度分别为(
)
A.和
B.和
C.和
D.和如图
2.
(2020·荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为(
)
A.20
B.30
C.40
D.50
3.
点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有(
)种
A.
B.
C.
D.
4.
关于?ABCD的叙述,正确的是( )
A.
若AB⊥BC,则?ABCD是菱形
B.
若AC⊥BD,则?ABCD是正方形
C.
若AC=BD,则?ABCD是矩形
D.
若AB=AD,则?ABCD是正方形
5.
(2020·广州)如图5,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
图5
A.
B.
C.
D.
6.
(2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
7.
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH=13S△DHC,其中结论正确的有( )
A.
1个
B.
2个
C.
3个
D.
4个
8.
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A.
2
B.
C.
D.
1
二、填空题
9.
如图,矩形ABCD的面积是15,边AB的长比AD的长大2,则AD的长是________.
10.
如图,,四边形和都是矩形,则等于
11.
如图,在菱形中,在上,点在上,则的最小值为
12.
某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
13.
如图,四边形为正方形,以为边向正方形外作正方形,与相交于点,则
14.
如图,正方形中,是对角线的交点,过点作,分别交于,若,则
三、解答题
15.
如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.
16.
如图,在中,,是的中点,连结,在的延长线上取一点,连结,.当与满足什么数量关系时,四边形是菱形?并说明理由.?
17.
如图,正方形中,是边上两点,且于,求证:
人教版
八年级数学
第18章
平行四边形
同步训练-答案
一、选择题
1.
【答案】B
2.
【答案】C
【解析】∵E,F分别是AD,BD的中点,∴EF是△DAB的中位线.∴AB=2EF=10.∵菱形的四边相等,∴菱形ABCD的周长=4AB=40.故选C.
3.
【答案】B
4.
【答案】C 【解析】逐项分析如下表:
选项
逐项分析
正误
A
有一个角是直角的平行四边形是矩形,不是菱形
×
B
对角线互相垂直的平行四边形是菱形,不一定是正方形
×
C
对角线相等的平行四边形是矩形
√
D
有一组邻边相等的平行四边形是菱形,不一定是正方形
×
5.
【答案】C
【解析】本题考查了矩形的性质,由勾股定理可得AC=10,再由矩形的对角线相等且互相平分的性质可得,OA=OD=5.
△ABD的面积为24,OA为△ABD
的中线,由中线等分面积可得,△AOD的面积为12.再由等面积法即可得OE+EF的值.过程如下:
∵
∴
即,∴OE+EF=,因此本题选C.
6.
【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7.
【答案】D 【解析】逐项分析如下表:
序号
逐项分析
正误
①
在正方形ABCD中,AB=BC=CD=DA,∠DAB=∠B=∠BCD=∠CDA=90°,∠ACB=∠ACD=45°,∵EF∥AD,∴四边形EFDA、四边形EFCB是矩形,∴∠EFC=∠ADC=90°,EF=DC,在Rt△CGF中,∠ACD=45°,∴GF=CF,∴EF-GF=CD-CF,即EG=DF
√
②
∵△GFC是等腰直角三角形,H是CG的中点,∴GH=FH,∠HGF=∠GFH=45°,∴∠EGH=∠DFH=135°,又由①知EG=DF,∴△EGH≌△DFH(SAS),∴∠HEF=∠FDH,∵∠AEH=∠AEF+∠HEF=90°+∠HEF,∠ADH=∠ADC-∠FDH=90°-∠FDH,∴∠AEH+∠ADH=180°
√
③
由②可知EH=DH,FH=CH,又∵EF=DC,∴△EHF≌△DHC(SSS)
√
④
∵△EGH≌△DFH,∴EH=DH,∠EHG=∠DHF,∴∠EHG+∠AHD=∠DHF+∠AHD=90°,即∠EHD=∠AHF=90°,∴△EHD为等腰直角三角形,∵=,∴设AE=2x,AB=3x,则DE==x,∴EH=DH=×x=x,∴S△EDH=EH2=×x2=x2.
在△DHC中,设CD边上的高为h,则h=CF=,则S△DHC=CD·h=×3x×=x2,==,即3S△EDH=13S△DHC
√
8.
【答案】B 【解析】∵AB=2,∴BF=2,又∵BM=BC=1,由勾股定理得FM==.
二、填空题
9.
【答案】3 【解析】本题主要考查了一元二次方程的实际应用问题.
设AD=x,由题知,AB=x+2,又∵矩形ABCD的面积为15,则x(x+2)=15,得到x2+2x-15=0,解得,x1=-5(舍)
,
x2=3,∴AD=3.
10.
【答案】
11.
【答案】
【解析】关于对称,连交于,且
为最小值
12.
【答案】
【解析】由图形可知:可推出
13.
【答案】
【解析】,故
14.
【答案】
三、解答题
15.
【答案】
解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,∴∠FAE=∠CDE,
∵E是AD的中点,∴AE=DE,
又∵∠FEA=∠CED,∴△FAE≌△CDE,∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形.
(2)BC=2CD.理由:
∵CF平分∠BCD,∴∠DCE=45°,
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,∴AD=2CD,
∵AD=BC,∴BC=2CD.
16.
【答案】
当(或或)时,四边形是菱形
理由如下:?
∵,∴
又点为中点,∴
∴四边形为平行四形边
∵
∴四边形为菱形
17.
【答案】
延长至点,使连结,由,得,进而推证,
18.2 特殊的平行四边形
一、选择题
1.已知矩形ABCD的对角线AC,BD相交于点O,
∠ADB=30°,AB=2,则OC的长是(
)
(A)1
(B)2
(C)4
(D)2
2.下列说法中正确的是(
)
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
3.如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是(
)
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
(A)①②
(B)①④
(C)①③④
(D)②③④
4.一个菱形的周长是20
cm,两条对角线的比是4∶3,则这个菱形的面积是(
)
(A)12
cm2
(B)96
cm2
(C)48
cm2
(D)24
cm2
5.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,则∠EBF的度数是(
)
A.75°
B.60°
C.50°
D.45°
6.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是(
)
(A)15
(B)16
(C)19
(D)20
7.已知?ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是(
)
A.∠BAC=∠DCA
B.∠BAC=∠DAC
C.∠BAC=∠ABD
D.∠BAC=∠ADB
8.平行四边形、矩形、菱形、正方形共有的性质是(
)
(A)对角线相等
(B)对角线互相平分
(C)对角线互相垂直
(D)对角线互相垂直平分
9.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是(
)
A.8
B.6
C.4
D.2
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分
△AFC的面积为( )
(A)12
(B)10
(C)8
(D)6
二、填空题
11.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,
P,Q分别为AO,AD的中点,则PQ的长度为 .?
12.菱形ABCD的对角线分别为18
cm与12
cm,则此菱形的面积为
cm2.
13.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),
(-2,0),点D在y轴上,则点C的坐标是 .?
14.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是 .?
15.如图,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,AC=BD.试添加一个条件
,使四边形ABCD为矩形.
16.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .?
解答题
17.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足
为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
18.如图,在菱形ABCD中,点E,O,F分别是边AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.
19.如图,在?ABCD中,O为AC的中点,过点O作EF⊥AC与边AD,BC分别相交于点E,F,求证:四边形AECF是菱形.
20如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
参考答案
一、选择题
1.已知矩形ABCD的对角线AC,BD相交于点O,
∠ADB=30°,AB=2,则OC的长是( B )
(A)1
(B)2
(C)4
(D)2
2.下列说法中正确的是(D)
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
3.如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( B )
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
(A)①②
(B)①④
(C)①③④
(D)②③④
4.一个菱形的周长是20
cm,两条对角线的比是4∶3,则这个菱形的面积是( D )
(A)12
cm2
(B)96
cm2
(C)48
cm2
(D)24
cm2
5.如图,在菱形ABCD中,BE⊥AD于点E,BF⊥CD于点F,且AE=DE,则∠EBF的度数是(B)
A.75°
B.60°
C.50°
D.45°
6.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( A )
(A)15
(B)16
(C)19
(D)20
7.已知?ABCD,AC,BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是(C)
A.∠BAC=∠DCA
B.∠BAC=∠DAC
C.∠BAC=∠ABD
D.∠BAC=∠ADB
8.平行四边形、矩形、菱形、正方形共有的性质是( B )
(A)对角线相等
(B)对角线互相平分
(C)对角线互相垂直
(D)对角线互相垂直平分
9.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是(C)
A.8
B.6
C.4
D.2
10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分
△AFC的面积为( B )
(A)12
(B)10
(C)8
(D)6
二、填空题
11.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,
P,Q分别为AO,AD的中点,则PQ的长度为 2.5 .?
12.菱形ABCD的对角线分别为18
cm与12
cm,则此菱形的面积为108__cm2.
13.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),
(-2,0),点D在y轴上,则点C的坐标是 (-5,4) .?
14.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是 ①②③④ .?
15.如图,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,AC=BD.试添加一个条件答案不唯一,如:AB∥CD,使四边形ABCD为矩形.
16.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 (-1,5) .?
解答题
17.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足
为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
(1)证明:在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF,
又∵DF⊥AE,
∴∠DFA=90°,
∴∠DFA=∠B,
又∵AD=EA,
∴△ADF≌△EAB,
∴DF=AB.
(2)解:∵∠ADF+∠FDC=90°,
∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴AD=2DF,
∵DF=AB,
∴AD=2AB=8.
18.如图,在菱形ABCD中,点E,O,F分别是边AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.
解:(1)证明:∵四边形ABCD为菱形,
∴AB=BC=CD=DA,
∠B=∠D.
又∵E,F分别是AB,AD的中点,
∴BE=DF.
∴△BCE≌△DCF(SAS).
(2)若AB⊥BC,则四边形AEOF为正方形,理由如下:
∵E,O分别是AB,AC的中点,∴EO∥BC.
又BC∥AD,∴OE∥AD.∴OE∥AF.
同理可证OF∥AE,
∴四边形AEOF为平行四边形.
由(1)可得AE=AF,
∴四边形AEOF为菱形.
∵AB⊥BC,∴∠BAD=90
°.
∴菱形AEOF为正方形.
19.如图,在?ABCD中,O为AC的中点,过点O作EF⊥AC与边AD,BC分别相交于点E,F,求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD.
∴AE∥CF.
∴∠OAE=∠OCF.
∵点O是AC的中点,∴OA=OC.
在△AOE和△COF中,
∴△AOE≌△COF(ASA).
∴AE=CF.
又∵AE∥CF,
∴四边形AECF是平行四边形.
∵EF与AC垂直,
∴四边形AECF是菱形.
20如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
解:∵四边形ABCD是菱形,BD=4,
∴OA=OC=AC,OB=OD=BD=2,AC⊥BD.
∵在Rt△OCD中,∠ACD=30
°,
∴CD=2OD=4,
OC===2.
∴AC=2OC=4.
∴S菱形ABCD=AC·BD=×4×4=8.
