6.4二次函数的应用

(共19张PPT)
数学九年级下：6.4《二次函数的应用》
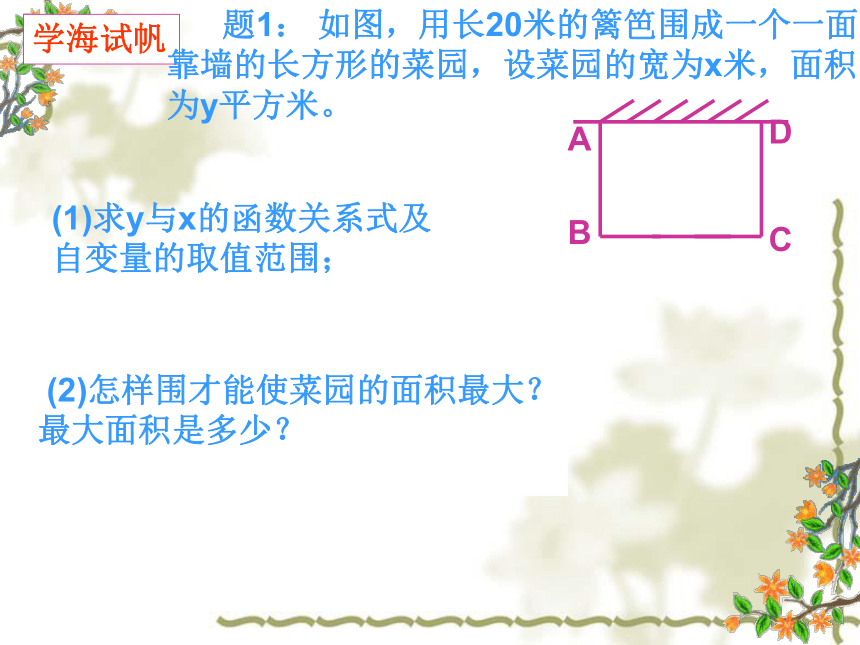
(1)求y与x的函数关系式及
自变量的取值范围；
(2)怎样围才能使菜园的面积最大？
最大面积是多少？
学海试帆
题1： 如图，用长20米的篱笆围成一个一面靠墙的长方形的菜园，设菜园的宽为x米，面积为y平方米。
A
B
C
D
y
0
x
5
10
15
20
25
30
1
2
3
4
5
7
8
9
1o
-1
6
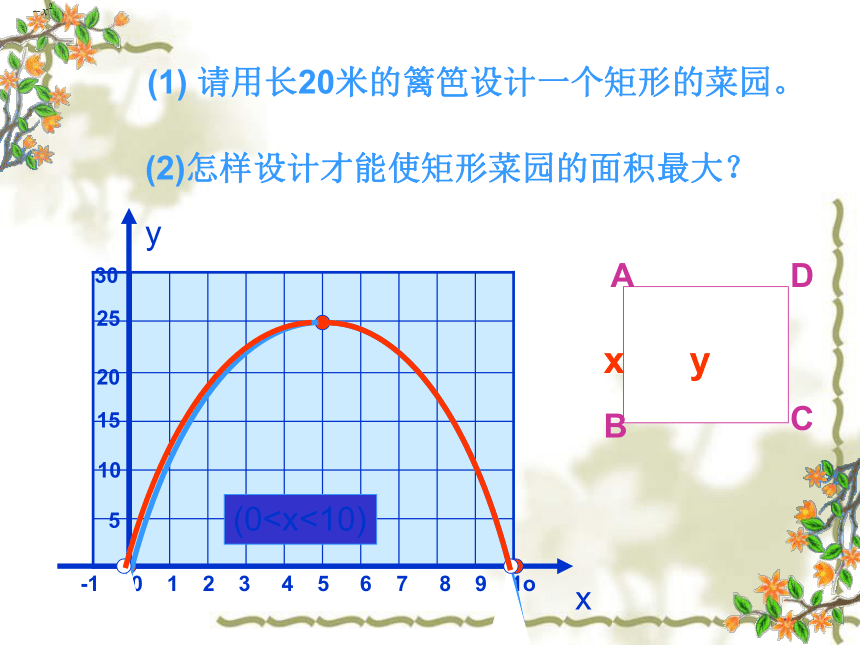
(1) 请用长20米的篱笆设计一个矩形的菜园。
(2)怎样设计才能使矩形菜园的面积最大？
A
B
C
D
x
y
(0题2：如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。
A
B
C
D
解：
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
(2)当x＝ 时，S最大值＝ ＝36（平方米）
∴ S＝x（24－4x）
＝－4x2＋24 x （0∴ 0<24－4x ≤6 4≤x<6
∴当x＝4cm时，S最大值＝32 平方米
学海探航
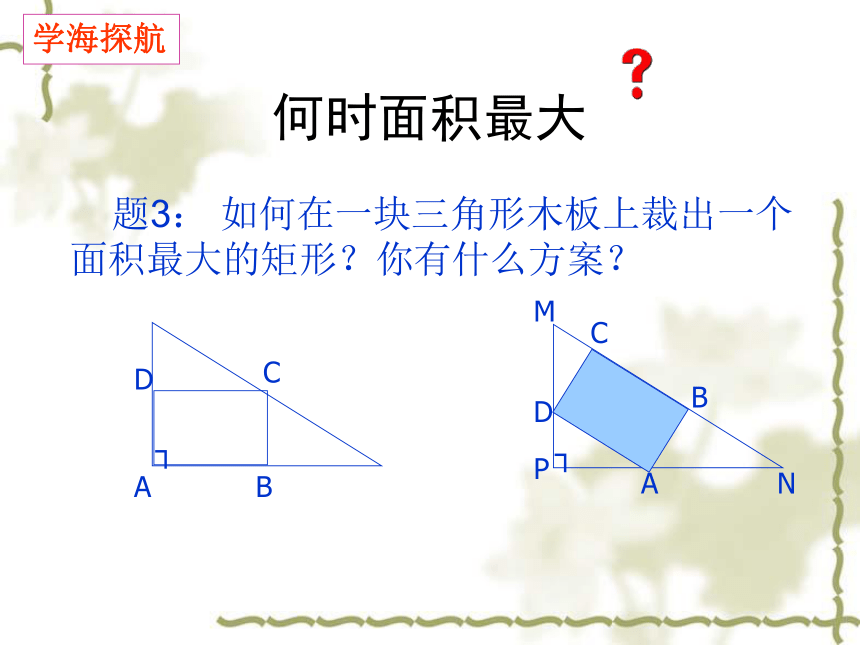
何时面积最大
题3： 如何在一块三角形木板上裁出一个面积最大的矩形？你有什么方案？
A
B
C
D
┐
A
B
C
D
┐
M
N
P
学海探航
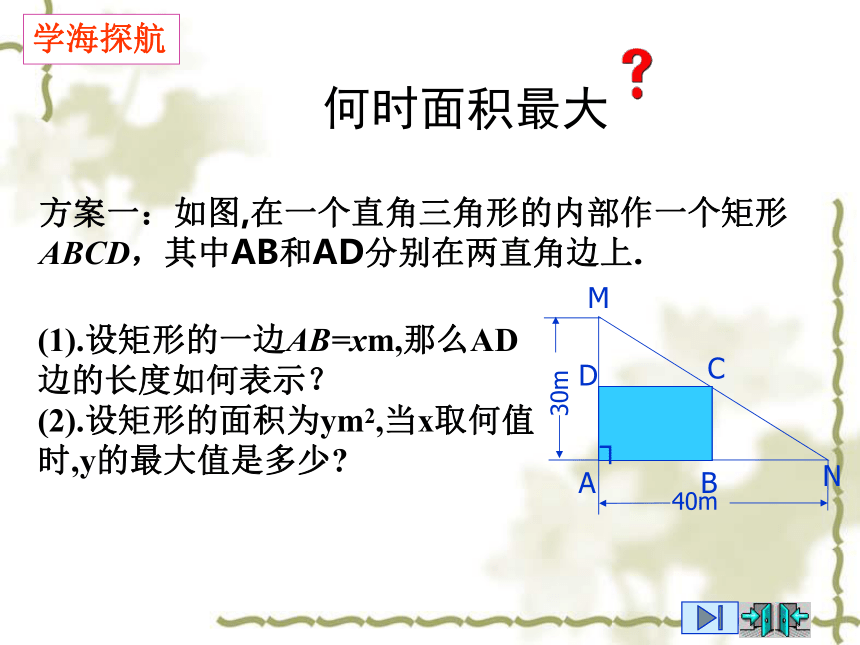
(1).设矩形的一边AB=xm,那么AD边的长度如何表示？
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
何时面积最大
方案一：如图,在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上.
M
N
40m
30m
A
B
C
D
┐
学海探航
(1).设矩形的一边BC=xm,那么AB边的长度如何表示？
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
何时面积最大
方案二：如图,在一个直角三角形的内部作一个矩形ABCD，其顶点A和点D分别在两直角边上,BC在斜边上.
A
B
C
D
┐
M
N
P
40m
30m
xm
bm
H
G
┛
┛
学海探航
何时窗户通过的光线最多
题4：某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
x
x
y
学海探航
何时面积最大
1.某工厂为了存放材料，需要围一个周长160米的矩形场地，问矩形的长和宽各取多少米，才能使存放场地的面积最大。
2.窗的形状是矩形上面加一个半圆。窗的周长等于6cm，要使窗能透过最多的光线，它的尺寸应该如何设计？
B
C
D
A
O
学海弄潮
3.用一块宽为1.2m的长方形铁板弯起两边做一个水槽，请比较下列方案中，水槽的横断面面积。
A
D
120
B
C
方案一
A
B
C
D
方案二
学海弄潮
5.在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发，沿AB边向点B以1cm/秒的速度移动，同时，点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动，回答下列问题：
（1）运动开始后第几秒时， △PBQ的面积等于8cm2
（2）设运动开始后第t秒时， 五边形APQCD的面积为Scm2， 写出S与t的函数关系式， 并指出自变量t的取值范围；
t为何值时S最小？求出S的最小值。
Q
P
C
B
A
D
例2.如图，在平面直角坐标系中，四边形OABC为菱形，点C的坐标为(4,0)，∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).　
(1)求A、B两点的坐标；
（2)设△OMN的面积为S，直线l运动时间为t秒(0≤t≤6)，试求S 与t的函数表达式；
(3)在题(2)的条件下，t为何值时，S的面积最大？最大面积是多少？
学海远征
.二次函数y=ax +bx+c的图象的一部分如图所示，已知它的顶点M在第二象限，且经过点A（1，0）和点B（0，1）。（04杭州）
（1）请判断实数a的取值范围，并说明理由；
2
x
y
1
B
1
A
O
5
4
（2）设此二次函数的图象
与x轴的另一个交点为C，
当△AMC的面积为△ABC
的 倍时，求a的值。
-1＜a＜0
学海远征
1.理解问题;
“二次函数应用” 的思路
回顾上一节“最大利润”和本节“最大面积”解决问题的过程，你能总结一下解决此类问题的基本思路吗？与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性,拓展等.
学海归舟
生活是数学的源泉.