北师大版八年级上册第四章一次函数专题—求一次函数的解析式及常见题型总结
文档属性
| 名称 | 北师大版八年级上册第四章一次函数专题—求一次函数的解析式及常见题型总结 |

|
|
| 格式 | zip | ||
| 文件大小 | 302.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 00:00:00 | ||
图片预览




文档简介
求一次函数的解析式及常见题型总结
求一次函数的表达式
求一次函数的解析式,就是求出的值,然后代入解析式即可.
常用待定系数法求一次函数的解析式.
待定系数法
用待定系数法求一次函数的解析式的一般步骤:
(1)设一次函数的解析式为,其中是待定的系数;
(2)将已知点的坐标代入函数解析式,建立关于的方程(组);
(3)解方程(组),求出待定系数的值;
(4)将求出的的值代回所设的函数解析式,即得到所求的函数解析式.
待定系数法的原理
即下面的结论:
点P与直线的关系:
(1)如果点P在直线上,那么的值必满足函数解析式,即;
(2)如果是满足函数解析式的一对对应值,那么以为坐标的点P必在直线上.
注意:
(1)对于一次函数,待定系数有两个,分别是,如果其中一个系数的值知道或确定,那么只需要将其图象上一个点的坐标代入函数解析式即可求出另一个系数的值;如果的值都不知道,则需要其图象上两个点的坐标代入求解.
(2)在解关于的二元一次方程组时,使用加减消元法进行.
(3)在求分段函数的解析式时,要在每段解析式的后面注明相应的自变量的取值范围.
(4)求函数的解析式是河南中考的重点,涉及到求一次函数、反比例函数和二次函数的解析式,难度不高.
例1.
若一次函数的图象经过和两点,求这个一次函数的表达式,并说出它的增减性.
分析:因为点在直线上,所以点的坐标满足函数关系式,利用待定系数法,可求出它的关系式,再由的符号得出它的增减性.
的符号决定一次函数图象的升降和函数的增减性.
解:
设这个一次函数的表达式为
∵该函数的图象经过和两点
∴
解之得:
∴该一次函数的表达式为.
∵
∴随的增大而增大.
例2.
已知一次函数的图象经过点和点,求当时的函数值.
分析:要想求出当时的函数值,就必须求出该一次函数的表达式,然后代入求值.由于该一次函数的表达式已经给出,所以在求解的第一步就不用在设表达式了.
解:∵一次函数的图象经过点和点
∴
解之得:
∴该一次函数的表达式为.
当时,.
例3.
已知直线经过点,求该直线的表达式.
分析:在该直线的表达式中,只有一个待定系数,所以只需要其图象上一个点的坐标即可,当然,建立的是关于的一元一次方程.
解:∵直线经过点
∴
解之得:
∴该直线的表达式为.
回答:对于该一次函数,因为_________0,所以该函数的图象是_________,(填“上升”或“下降”)随的增大而_________,图象不经过第_________象限.
习题1.
已知一次函数的图象经过点A,B,C,求这个一次函数的表达式,并求出的值.
习题2.
已知直线经过点和,求这条直线的函数表达式;当该直线上有一点P的纵坐标是2时,求P点的横坐标.
专题
求一次函数的表达式的类型及方法
类型一、定义型
例4.
已知函数是一次函数,求这个函数的关系式.
分析:根据一次函数关系式的自变量的系数,自变量的次数为1,可得关于的表达式和方程,即可求得的值,继而可得到函数关系式.
解:由题意可知:
解之得:.
∴这个函数的关系式为.
习题3.
已知是一次函数,求这个函数的关系式.
类型二、两点型
知道一次函数的图象经过的两个点的坐标,用待定系数法求其函数关系式.
例5.
已知一次函数的图象经过点和点,求该一次函数的关系式.
解:设该一次函数的关系式为
∵该函数的图象经过点和点
∴
解之得:
∴该函数的关系式为.
习题4.
已知一次函数的图象经过,两点.
(1)求这个一次函数的关系式;
(2)试判断点是否在这个一次函数的图象上.
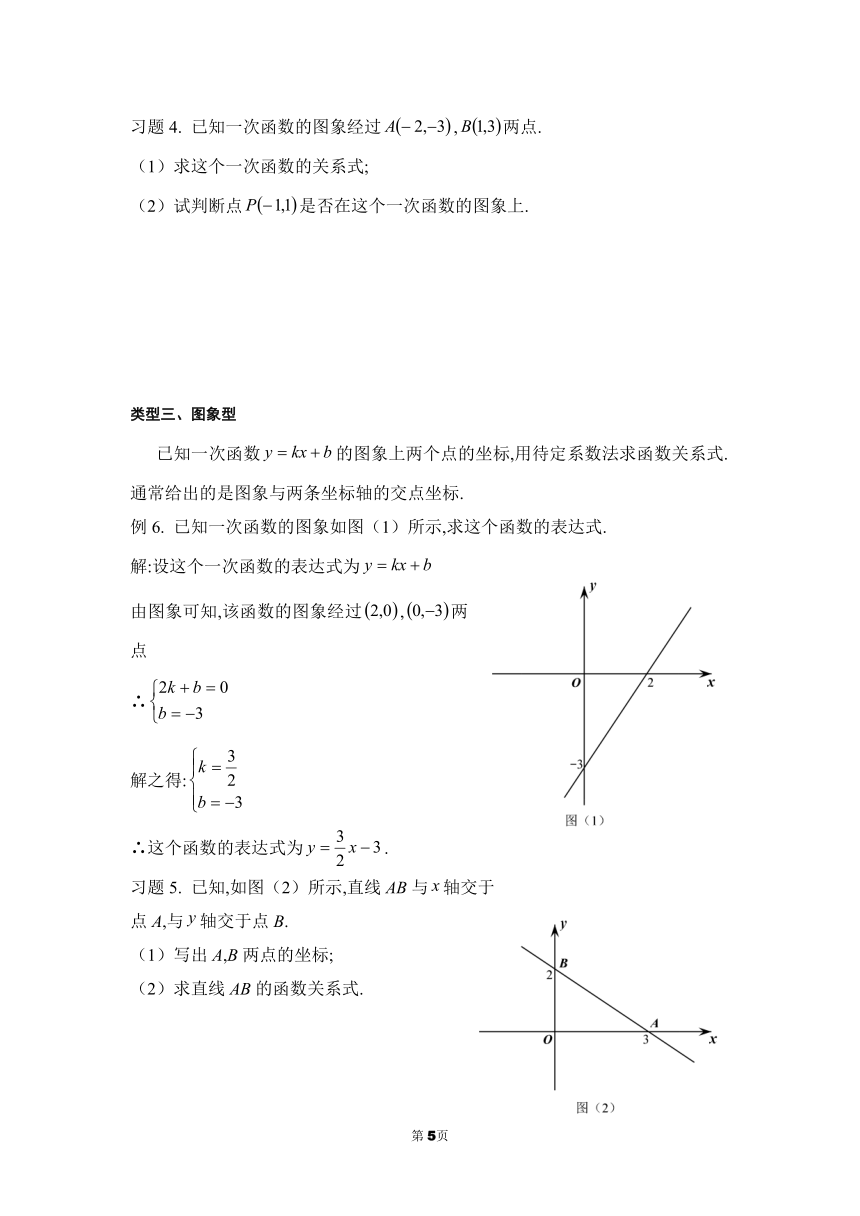
类型三、图象型
已知一次函数的图象上两个点的坐标,用待定系数法求函数关系式.通常给出的是图象与两条坐标轴的交点坐标.
例6.
已知一次函数的图象如图(1)所示,求这个函数的表达式.
解:设这个一次函数的表达式为
由图象可知,该函数的图象经过,两点
∴
解之得:
∴这个函数的表达式为.
习题5.
已知,如图(2)所示,直线AB与轴交于
点A,与轴交于点B.
(1)写出A,B两点的坐标;
(2)求直线AB的函数关系式.
类型四、平行型
若两个一次函数的图象互相平行,则它们的值相等,值不相等.据此可用来确定系数的值.
例7.
已知一次函数的图象平行于直线,且经过点,求这个一次函数的关系式.
分析:根据两条直线的平行关系确定的值,然后再根据一个点的坐标代入求出的值.
解:由题意可知:
∴
∵该函数的图象经过点
∴
∴这个一次函数的关系式为.
习题6.
一次函数的图象与轴交于点,且与直线平行,求它的函数表达式.
类型五、相交型
同一平面内两条直线的位置关系有两种:平行和相交.确定相交的两条直线的函数关系式,要明确交点的意义,即两个一次函数图象的交点的横坐标和纵坐标,是由这两条直线的关系式组成的方程组的解.
例8.
已知一次函数的图象经过点,并且与直线相交与轴上一点,求这个一次函数的关系式.
分析:本题中的一个条件是直线与轴的交点,只要求出这个交点的坐标,再把交点坐标和分别代入所设函数关系式中,便可求解.
解:设这个一次函数的关系式为
∵直线与轴的交点是
∴这个一次函数的图象与轴的交点是
把和分别代入得:
解之得:.
∴这个一次函数的关系式为.
习题7.
已知三条直线和相交于一点,求该交点的坐标和第三条直线的表达式.
分析:该交点的横坐标、纵坐标是方程组的解.
类型六、面积型
给出的条件中有直线的坐标三角形的面积,求直线的解析式,注意分类讨论.
例9.
直线经过点,且与坐标轴所围成的直角三角形的面积为,求直线的解析式.
分析:题中的三角形就是坐标三角形,它是直角三角形,两条直角边的长度隐含在一次函数的图象与两条坐标轴的交点坐标中:与轴的交点的横坐标的绝对值是其中一条直角边的长,与轴的交点的纵坐标的绝对值是另一条直角边的长.
解:直线与轴的交点坐标为
由题意可知:
∴,
∴或
∵直线经过点
∴,或
解之得:或
∴该直线的解析式为或.
例10.
如图(3)所示,在平面直角坐标系中,一次函数的图象分别与轴、轴交于点A、B,点P在轴上,若,求直线PB对应的函数关系式.
分析:根据题意可得点P可以在轴左边,也可以在轴右边,应分两种情况讨论.先求点A和点B的坐标,然后根据确定点P的位置,进而运用待定系数法可求出直线PB对应的函数关系式.
解:令,;令,则,解之得:.
∴点A的坐标为,点B的坐标为
∵
∴,得
∴点P的坐标为或
设直线PB对应的函数关系式为
∴或
解之得:或
∴直线PB对应的函数关系式为或.
习题8.
已知一次函数的图象与轴交于点,与轴交于点B.若
△AOB的面积为12,求一次函数的关系式.
类型七、范围型
例11.
已知一次函数中,自变量的取值范围是≤≤4,相应函数值的范围是≤≤2,求此函数的表达式.
分析:本题分两种情况讨论:(1)随的增大而增大;(2)随的增大而减小.
解:分两种情况:
(1)当时,随的增大而增大,所以当时,;当时,.
∴
解之得:
∴此函数的表达式为;
(2)当时,随的增大而减小,所以当时,;当时,
.
∴,解之得:
∴此函数的表达式为.
综上所述,此函数的表达式为或.
习题9.
一次函数的自变量的取值范围是≤≤6,相应函数值的取值范围是≤≤,求这个函数的关系式.
类型八、表格型
例12.
某产品每件成本10元,试销阶段每件产品的销售价(元)与产品的日销售量(件)之间的关系如下表:
(元)
15
20
25
…
(件)
25
20
15
…
若日销售量是销售价的一次函数,求出日销售量(件)与销售价(元)的函数关系式.
解:设此一次函数的关系式为,则:
解之得:
∴此一次函数的关系式为.
习题10.
下表中,是的一次函数,求该函数的关系式,并补全下表.
0
1
2
2
6
其它
例13.
已知与成正比例,当时,,求与之间的函数关系式,并判断是的什么函数.
解:由题意可设
∵时,
∴,解之得:
∴与之间的函数关系式为
由关系式可知,是的一次函数.
习题11.
已知与成正比例,且当时,,求与之间的函数关系式,并求当时,的值.
习题12.
已知与成正比例,与成正比例,.当时,;当时,.求关于的函数关系式.
分析:由题意可设,.
第11页
求一次函数的表达式
求一次函数的解析式,就是求出的值,然后代入解析式即可.
常用待定系数法求一次函数的解析式.
待定系数法
用待定系数法求一次函数的解析式的一般步骤:
(1)设一次函数的解析式为,其中是待定的系数;
(2)将已知点的坐标代入函数解析式,建立关于的方程(组);
(3)解方程(组),求出待定系数的值;
(4)将求出的的值代回所设的函数解析式,即得到所求的函数解析式.
待定系数法的原理
即下面的结论:
点P与直线的关系:
(1)如果点P在直线上,那么的值必满足函数解析式,即;
(2)如果是满足函数解析式的一对对应值,那么以为坐标的点P必在直线上.
注意:
(1)对于一次函数,待定系数有两个,分别是,如果其中一个系数的值知道或确定,那么只需要将其图象上一个点的坐标代入函数解析式即可求出另一个系数的值;如果的值都不知道,则需要其图象上两个点的坐标代入求解.
(2)在解关于的二元一次方程组时,使用加减消元法进行.
(3)在求分段函数的解析式时,要在每段解析式的后面注明相应的自变量的取值范围.
(4)求函数的解析式是河南中考的重点,涉及到求一次函数、反比例函数和二次函数的解析式,难度不高.
例1.
若一次函数的图象经过和两点,求这个一次函数的表达式,并说出它的增减性.
分析:因为点在直线上,所以点的坐标满足函数关系式,利用待定系数法,可求出它的关系式,再由的符号得出它的增减性.
的符号决定一次函数图象的升降和函数的增减性.
解:
设这个一次函数的表达式为
∵该函数的图象经过和两点
∴
解之得:
∴该一次函数的表达式为.
∵
∴随的增大而增大.
例2.
已知一次函数的图象经过点和点,求当时的函数值.
分析:要想求出当时的函数值,就必须求出该一次函数的表达式,然后代入求值.由于该一次函数的表达式已经给出,所以在求解的第一步就不用在设表达式了.
解:∵一次函数的图象经过点和点
∴
解之得:
∴该一次函数的表达式为.
当时,.
例3.
已知直线经过点,求该直线的表达式.
分析:在该直线的表达式中,只有一个待定系数,所以只需要其图象上一个点的坐标即可,当然,建立的是关于的一元一次方程.
解:∵直线经过点
∴
解之得:
∴该直线的表达式为.
回答:对于该一次函数,因为_________0,所以该函数的图象是_________,(填“上升”或“下降”)随的增大而_________,图象不经过第_________象限.
习题1.
已知一次函数的图象经过点A,B,C,求这个一次函数的表达式,并求出的值.
习题2.
已知直线经过点和,求这条直线的函数表达式;当该直线上有一点P的纵坐标是2时,求P点的横坐标.
专题
求一次函数的表达式的类型及方法
类型一、定义型
例4.
已知函数是一次函数,求这个函数的关系式.
分析:根据一次函数关系式的自变量的系数,自变量的次数为1,可得关于的表达式和方程,即可求得的值,继而可得到函数关系式.
解:由题意可知:
解之得:.
∴这个函数的关系式为.
习题3.
已知是一次函数,求这个函数的关系式.
类型二、两点型
知道一次函数的图象经过的两个点的坐标,用待定系数法求其函数关系式.
例5.
已知一次函数的图象经过点和点,求该一次函数的关系式.
解:设该一次函数的关系式为
∵该函数的图象经过点和点
∴
解之得:
∴该函数的关系式为.
习题4.
已知一次函数的图象经过,两点.
(1)求这个一次函数的关系式;
(2)试判断点是否在这个一次函数的图象上.
类型三、图象型
已知一次函数的图象上两个点的坐标,用待定系数法求函数关系式.通常给出的是图象与两条坐标轴的交点坐标.
例6.
已知一次函数的图象如图(1)所示,求这个函数的表达式.
解:设这个一次函数的表达式为
由图象可知,该函数的图象经过,两点
∴
解之得:
∴这个函数的表达式为.
习题5.
已知,如图(2)所示,直线AB与轴交于
点A,与轴交于点B.
(1)写出A,B两点的坐标;
(2)求直线AB的函数关系式.
类型四、平行型
若两个一次函数的图象互相平行,则它们的值相等,值不相等.据此可用来确定系数的值.
例7.
已知一次函数的图象平行于直线,且经过点,求这个一次函数的关系式.
分析:根据两条直线的平行关系确定的值,然后再根据一个点的坐标代入求出的值.
解:由题意可知:
∴
∵该函数的图象经过点
∴
∴这个一次函数的关系式为.
习题6.
一次函数的图象与轴交于点,且与直线平行,求它的函数表达式.
类型五、相交型
同一平面内两条直线的位置关系有两种:平行和相交.确定相交的两条直线的函数关系式,要明确交点的意义,即两个一次函数图象的交点的横坐标和纵坐标,是由这两条直线的关系式组成的方程组的解.
例8.
已知一次函数的图象经过点,并且与直线相交与轴上一点,求这个一次函数的关系式.
分析:本题中的一个条件是直线与轴的交点,只要求出这个交点的坐标,再把交点坐标和分别代入所设函数关系式中,便可求解.
解:设这个一次函数的关系式为
∵直线与轴的交点是
∴这个一次函数的图象与轴的交点是
把和分别代入得:
解之得:.
∴这个一次函数的关系式为.
习题7.
已知三条直线和相交于一点,求该交点的坐标和第三条直线的表达式.
分析:该交点的横坐标、纵坐标是方程组的解.
类型六、面积型
给出的条件中有直线的坐标三角形的面积,求直线的解析式,注意分类讨论.
例9.
直线经过点,且与坐标轴所围成的直角三角形的面积为,求直线的解析式.
分析:题中的三角形就是坐标三角形,它是直角三角形,两条直角边的长度隐含在一次函数的图象与两条坐标轴的交点坐标中:与轴的交点的横坐标的绝对值是其中一条直角边的长,与轴的交点的纵坐标的绝对值是另一条直角边的长.
解:直线与轴的交点坐标为
由题意可知:
∴,
∴或
∵直线经过点
∴,或
解之得:或
∴该直线的解析式为或.
例10.
如图(3)所示,在平面直角坐标系中,一次函数的图象分别与轴、轴交于点A、B,点P在轴上,若,求直线PB对应的函数关系式.
分析:根据题意可得点P可以在轴左边,也可以在轴右边,应分两种情况讨论.先求点A和点B的坐标,然后根据确定点P的位置,进而运用待定系数法可求出直线PB对应的函数关系式.
解:令,;令,则,解之得:.
∴点A的坐标为,点B的坐标为
∵
∴,得
∴点P的坐标为或
设直线PB对应的函数关系式为
∴或
解之得:或
∴直线PB对应的函数关系式为或.
习题8.
已知一次函数的图象与轴交于点,与轴交于点B.若
△AOB的面积为12,求一次函数的关系式.
类型七、范围型
例11.
已知一次函数中,自变量的取值范围是≤≤4,相应函数值的范围是≤≤2,求此函数的表达式.
分析:本题分两种情况讨论:(1)随的增大而增大;(2)随的增大而减小.
解:分两种情况:
(1)当时,随的增大而增大,所以当时,;当时,.
∴
解之得:
∴此函数的表达式为;
(2)当时,随的增大而减小,所以当时,;当时,
.
∴,解之得:
∴此函数的表达式为.
综上所述,此函数的表达式为或.
习题9.
一次函数的自变量的取值范围是≤≤6,相应函数值的取值范围是≤≤,求这个函数的关系式.
类型八、表格型
例12.
某产品每件成本10元,试销阶段每件产品的销售价(元)与产品的日销售量(件)之间的关系如下表:
(元)
15
20
25
…
(件)
25
20
15
…
若日销售量是销售价的一次函数,求出日销售量(件)与销售价(元)的函数关系式.
解:设此一次函数的关系式为,则:
解之得:
∴此一次函数的关系式为.
习题10.
下表中,是的一次函数,求该函数的关系式,并补全下表.
0
1
2
2
6
其它
例13.
已知与成正比例,当时,,求与之间的函数关系式,并判断是的什么函数.
解:由题意可设
∵时,
∴,解之得:
∴与之间的函数关系式为
由关系式可知,是的一次函数.
习题11.
已知与成正比例,且当时,,求与之间的函数关系式,并求当时,的值.
习题12.
已知与成正比例,与成正比例,.当时,;当时,.求关于的函数关系式.
分析:由题意可设,.
第11页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
