人教版九年级下册数学 27.2.3相似三角形应用举例(2) 学案
文档属性
| 名称 | 人教版九年级下册数学 27.2.3相似三角形应用举例(2) 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 138.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 00:00:00 | ||
图片预览

文档简介
27.2.3相似三角形应用举例(2)
一、学习目标:
进一步巩固相似三角形的知识。
能够运用相似三角形的知识,解决不能直接测量物体的长度和高度(如盲区问题)等。
能够把实际问题转化为有关相似三角形的数学模型,进一步了解数学建模思想。
二、课前回顾
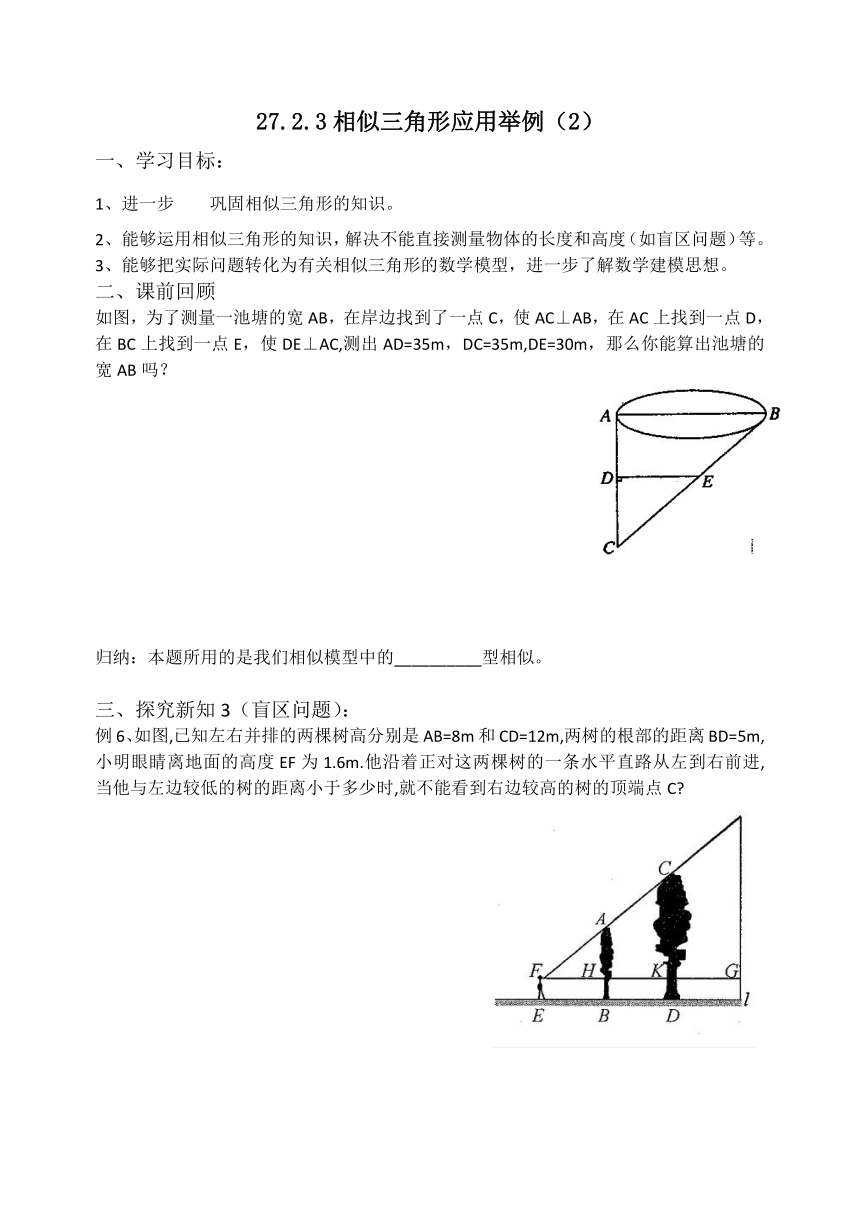
如图,为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=35m,DC=35m,DE=30m,那么你能算出池塘的宽AB吗?
归纳:本题所用的是我们相似模型中的__________型相似。
三、探究新知3(盲区问题):
例6、如图,已知左右并排的两棵树高分别是AB=8m和CD=12m,两树的根部的距离BD=5m,小明眼睛离地面的高度EF为1.6m.他沿着正对这两棵树的一条水平直路从左到右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?
跟踪训练:
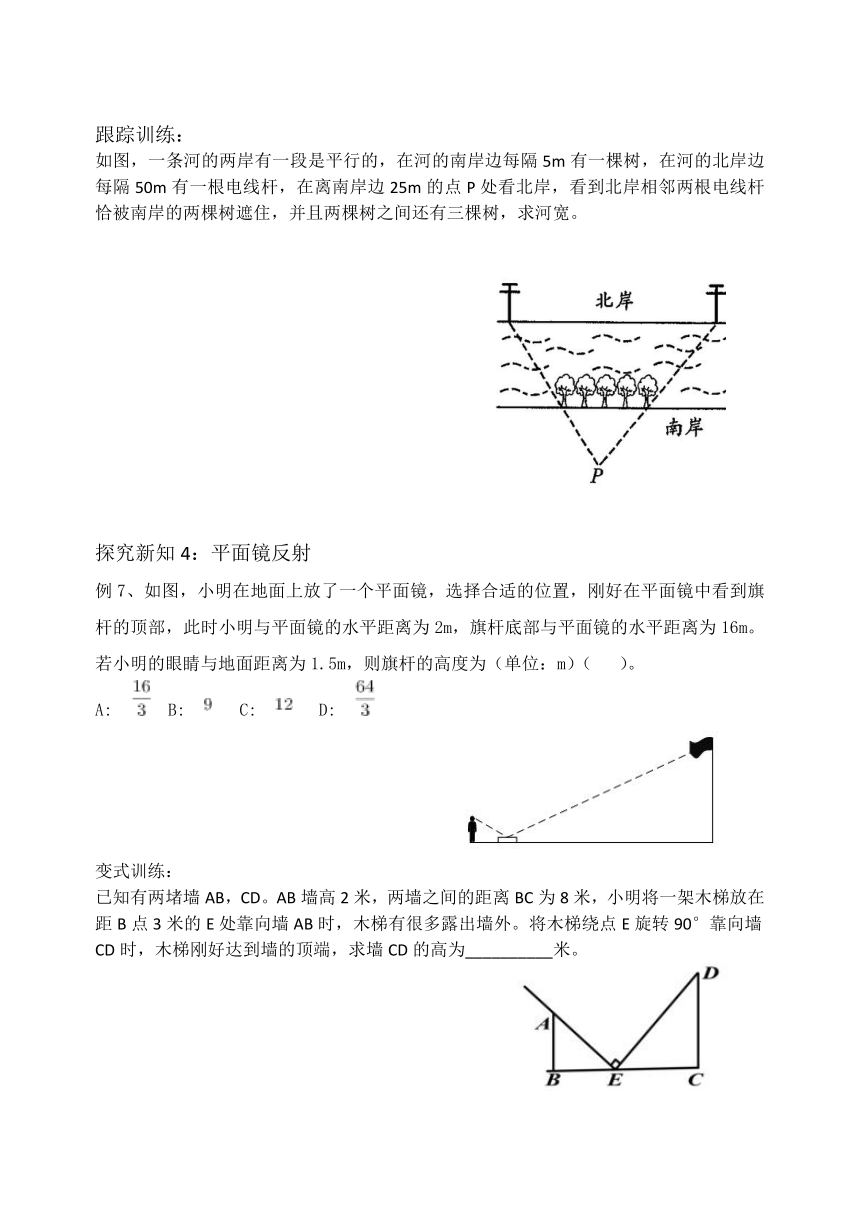
如图,一条河的两岸有一段是平行的,在河的南岸边每隔5m有一棵树,在河的北岸边每隔50m有一根电线杆,在离南岸边25m的点P处看北岸,看到北岸相邻两根电线杆恰被南岸的两棵树遮住,并且两棵树之间还有三棵树,求河宽。
探究新知4:平面镜反射
例7、如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m。若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)(
?)。
A:?
B:?
C:?
D:?
变式训练:
已知有两堵墙AB,CD。AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外。将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,求墙CD的高为__________米。
四、拓展应用
1、如图所示,零件的外径为a=25cm,要求它的厚度x,需要求出内孔的直径AB,但不能直接量出AB,现用一个交叉钳(两臂长AC和BD相等)去量,如果OA∶OC=OB∶OD=3,且量得CD=7cm,求AB以及零件厚度x.
如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
当堂达标
如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为?_________cm。
2、如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
3、如图,△ABC是一块锐角三角形材料,BC=120mm,高,AD=80mm要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,矩形PQMN的面积为S,求S关于x的函数表达式,并指出x的取值范围.
(2)当x为何值时,矩形PQMN的面积最大?最大值是多少?
一、学习目标:
进一步巩固相似三角形的知识。
能够运用相似三角形的知识,解决不能直接测量物体的长度和高度(如盲区问题)等。
能够把实际问题转化为有关相似三角形的数学模型,进一步了解数学建模思想。
二、课前回顾
如图,为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=35m,DC=35m,DE=30m,那么你能算出池塘的宽AB吗?
归纳:本题所用的是我们相似模型中的__________型相似。
三、探究新知3(盲区问题):
例6、如图,已知左右并排的两棵树高分别是AB=8m和CD=12m,两树的根部的距离BD=5m,小明眼睛离地面的高度EF为1.6m.他沿着正对这两棵树的一条水平直路从左到右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?
跟踪训练:
如图,一条河的两岸有一段是平行的,在河的南岸边每隔5m有一棵树,在河的北岸边每隔50m有一根电线杆,在离南岸边25m的点P处看北岸,看到北岸相邻两根电线杆恰被南岸的两棵树遮住,并且两棵树之间还有三棵树,求河宽。
探究新知4:平面镜反射
例7、如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m。若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)(
?)。
A:?
B:?
C:?
D:?
变式训练:
已知有两堵墙AB,CD。AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外。将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,求墙CD的高为__________米。
四、拓展应用
1、如图所示,零件的外径为a=25cm,要求它的厚度x,需要求出内孔的直径AB,但不能直接量出AB,现用一个交叉钳(两臂长AC和BD相等)去量,如果OA∶OC=OB∶OD=3,且量得CD=7cm,求AB以及零件厚度x.
如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
当堂达标
如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为?_________cm。
2、如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
3、如图,△ABC是一块锐角三角形材料,BC=120mm,高,AD=80mm要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
(1)设PN=x,矩形PQMN的面积为S,求S关于x的函数表达式,并指出x的取值范围.
(2)当x为何值时,矩形PQMN的面积最大?最大值是多少?
